用逆变换采样方法构建随机变量生成器
上期 从零构建统计随机变量生成器之离散基础篇,我们从零出发构建了基于伯努利的基础离散分布,这一期我们来详细介绍广泛使用的 Inverse Transform Method(逆变换采样方法)。
- 从零构建统计随机变量生成器之 离散基础篇
- 从零构建统计随机变量生成器之 用逆变换采样方法构建随机变量生成器
- 深入 LeetCode 470 拒绝采样,状态转移图求期望和一道经典统计求期望题目
- 从零构建统计随机变量生成器之 正态分布 Box-Muller方法
逆变换采样方法
Inverse Transform Method 是最基础常见的方法,可用于离散分布和连续分布。常见的分布一般都能通过此方法生成,只需要随机变量CDF的解析表达式。假设随机变量 \(X\),其CDF为 \(F^{-1}\),则 Inverse Transform Method 仅有两步
- 通过生成 [0, 1] 之间的均匀随机数 \(u\)
- 代入 \(F^{-1}\) 即产生满足\(X\)分布的实例 \(x = F^{-1}(u)\)
离散例子
我们先举一个离散分布来直观感受一下其工作机制。有如下PMF的离散类别分布,范围在 [1, 5]。 \[ P(X = 1)=\frac{1}{15} \]
\[ P(X = 2)=\frac{2}{15} \]
\[ P(X = 3)=\frac{1}{5} \]
\[ P(X = 4)=\frac{4}{15} \]
\[ P(X = 5)=\frac{1}{3} \]
转换成CDF为
\[ P(X \leq 1)=\frac{1}{15} \]
\[ P(X \leq 2)=\frac{1}{15}+\frac{2}{15}=\frac{1}{5} \]
\[ P(X \leq 3)=\frac{1}{15}+\frac{2}{15}+\frac{1}{5}=\frac{6}{15} \]
\[ P(X \leq 4)=\frac{1}{15}+\frac{2}{15}+\frac{1}{5}+\frac{4}{15}=\frac{2}{3} \]
\[ P(X \leq 5)=\frac{1}{15}+\frac{2}{15}+\frac{1}{5}+\frac{4}{15}+\frac{1}{3}=1 \]
画出对应的CDF图
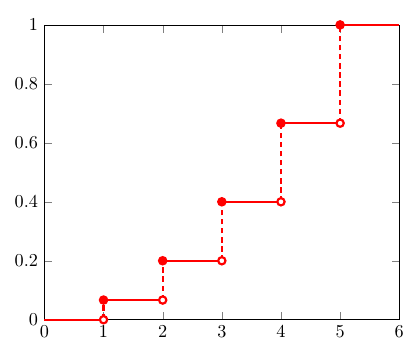
那么Inverse Transformation Method 的第一步,随机生成 0-1 之间的数 u,可以直观的认为是在 y 轴上生成一个随机的点 u。注意到5段竖虚线对应了5个离散的取值,它们的长度和为1,并且每一段长度代表了每个值的权重。因此,通过在 y 轴上的均匀采样可以生成给定PMF的 x 的分布。
离散分布的逆变换采样方法用数学公式可以表述为:找到第一个 x,其CDF的范围包括了 u,即
\[ F^{-1}(u)=\min \{x: F(x) \geq u\} \]
扩展到连续分布
有了离散类别分布的直观感受,扩展到连续分布也就不难理解了。类似于微积分中将连续空间做离散切分,再通过极限的方法,连续光滑函数在 y 轴上可以切分成长度为 \(\Delta u\) 的线段,那么生成的 x 值就是其近似值。随着 $ _{u } $,最终 $ x=F^{-1}(u) $ 即为满足要求的分布。
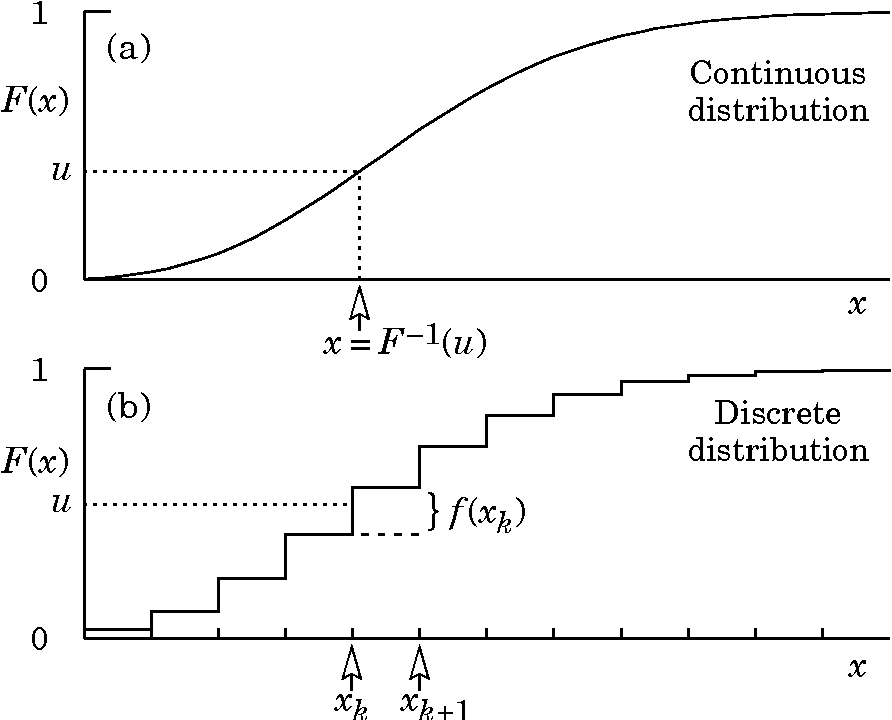
指数分布(连续)
以最为常见的指数分布为例,我们来看看具体的步骤。
我们知道指数分布的PDF如下
\[ f(x)=\left\{\begin{array}{ll}\lambda e^{-\lambda x}, & x \geq 0 \\ 0, & x<0\end{array}\right. \]
PDF 图为
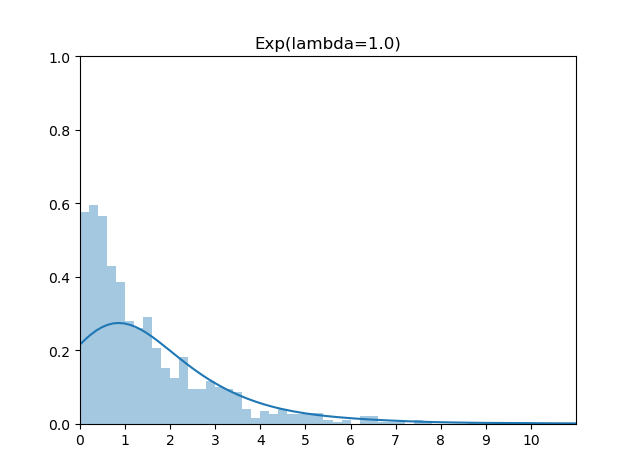
计算CDF为
\[ F(x)=\int_{-\infty}^{x} f(t) d t=\left\{\begin{array}{ll}1-e^{-\lambda x}, & x \geq 0 \\ 0, & x<0\end{array}\right. \]
CDF 图
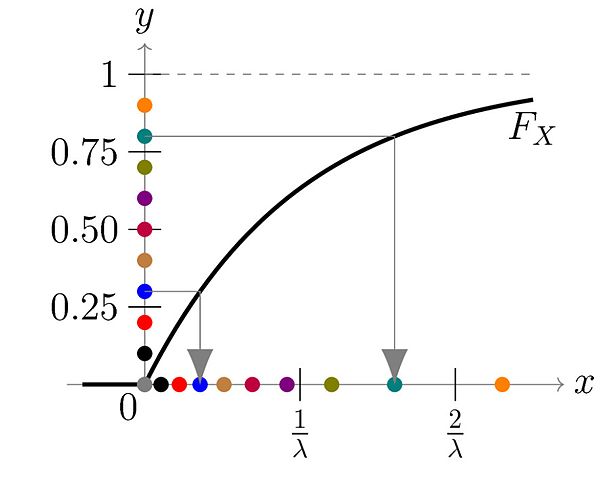
可以求得逆函数为
\[ x=F^{-1}(u)=-\frac{1}{\lambda} \ln (1-u) \]
由于 1-u 在 [0, 1] 范围上的随机数等价于 u,因此,x 的生成公式等价于
\[ x=-\frac{1}{\lambda} \ln (u) \]
实现代码
对应代码很简单
1 | import random |
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/coutinous_exp_inv.py
类别分布(离散)
我们再来看基于类别分布 Inverse Transformation Method的其他离散分布例子。在从零构建统计随机变量生成器之离散基础篇中,我们已经介绍了类别分布(Categorical Distribution)的逆变换采样算法,同时还介绍了通过模拟 Bernoulli 实验来生成二项,几何,超几何分布的方法。在这一篇中,我们通过逆变换采样算法再来生成这些分布。
先回顾一下类别分布的逆变换采样实现。
给定如下的类别分布, $p = [0.2, 0.3, 0.1, 0.4] $
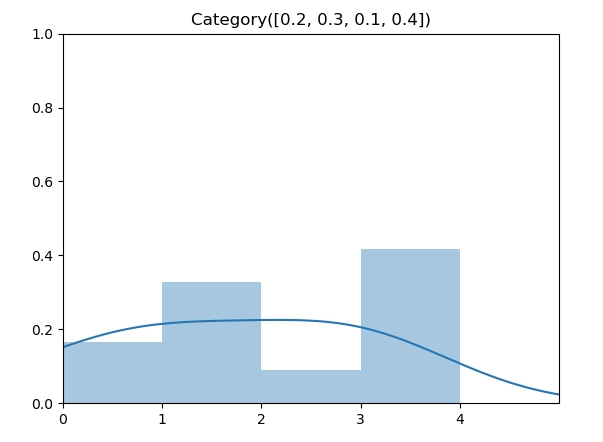
实现代码
类别分布的逆变换采样实现需要找到第一个大于 u 的元素的索引序号,在我们的实现中,将 $p = [0.2, 0.3, 0.1, 0.4] $ 转换成累计概率 $c = [0.2, 0.5, 0.6, 1] $ 后,由于 \(\vec c\) 数组是非递减的,因此我们可以用二分法代替线性查找,将时间复杂度降到 \(O(log(n))\)。下面的实现中直接调用 python bisect 函数即可。
1 | import bisect |
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_categorical.py
二项分布(离散)
二项分布(Binomial Distribution)有两个参数 n 和 p,表示伯努利实验做n次后成功的次数。图中为 n=6,p=0.5的二项分布。
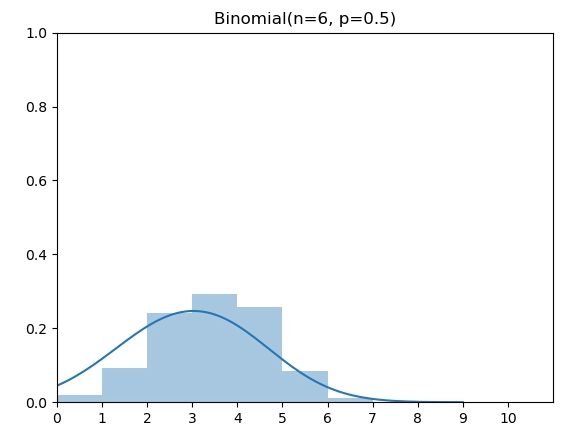
概率质量函数(PMF)
\[ \operatorname{P}_\text{Binomial}(X=k)=\left(\begin{array}{c}n \\ k\end{array}\right)p^{k}(1- p)^{n-k} \]
实现代码
根据上面的PMF定义,我们将 [0, 6] 上的PMF计算出来,然后调用类别分布的逆变换采样实现即可:
1 | from scipy.special import comb |
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_binomial_inv.py
超几何分布(离散)
同样的,超几何分布(HyperGeometric Distribution)也可以如法炮制。
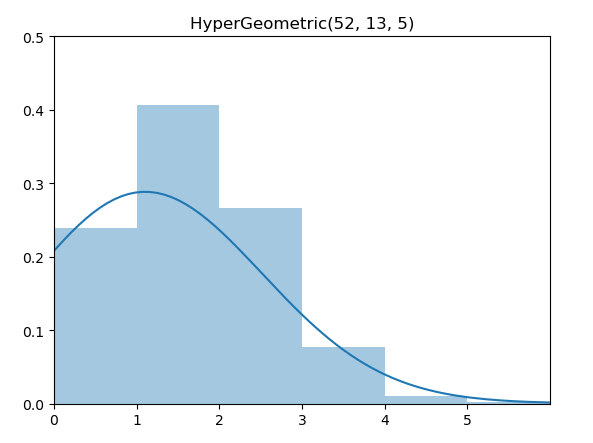
概率质量函数(PMF)
\[ \operatorname{P}_\text{Hypergeo}(X=k)=\frac{\left(\begin{array}{c}K \\ k\end{array}\right)\left(\begin{array}{c}N-k \\ n-k\end{array}\right)}{\left(\begin{array}{l}N \\ n\end{array}\right)} \]
实现代码
1 | from scipy.special import comb |
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_hypergeometric_inv.py
几何分布(离散)
几何分布(Geometric Distribution)和上面的二项分布以及超几何分布不同的是,它的 support 是所有非负整数,因此,我们无法穷举计算所有 x 的概率。但是,我们可以通过将CDF 推出 Inverse CDF的解析表达式来直接实现。
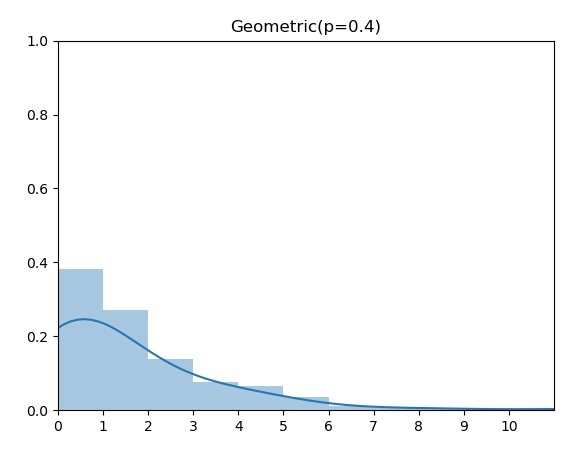
概率质量函数(PMF)
\[ \operatorname{P}_\text{Geometric}(X=k)=(1-p)^{k-1} p \]
CDF
\[ F_X(x) = 1- (1-p)^x \]
Inverse CDF
反函数求得为 \[ F^{-1}(u) = \lfloor { log(1-u) \over log(1-p) }\rfloor \]
实现代码
1 | import random |
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_geometric_inv.py
标准正态分布
一般,标准正态分布用Box-Muller 方法来生成,这个后续将做详细介绍。这里我们用 Schmeiser 提出的基于Inverse Transformation Method的近似方法来生成:
\[ X=F^{-1}(u) \approx \frac{u^{0.135}-(1-u)^{0.135}}{0.1975} \]
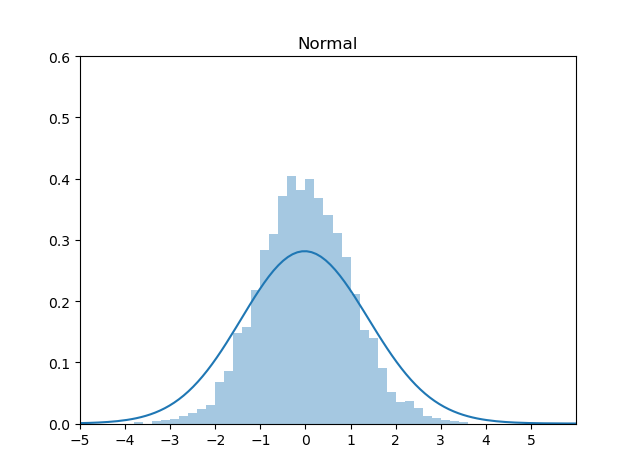
实现代码
1 | import random |
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/coutinous_normal_apprx.py
从零构建统计随机变量生成器之泊松分布
http://www.columbia.edu/~ks20/4404-Sigman/4404-Notes-ITM.pdf
https://www.win.tue.nl/~marko/2WB05/lecture8.pdf
泊松分布
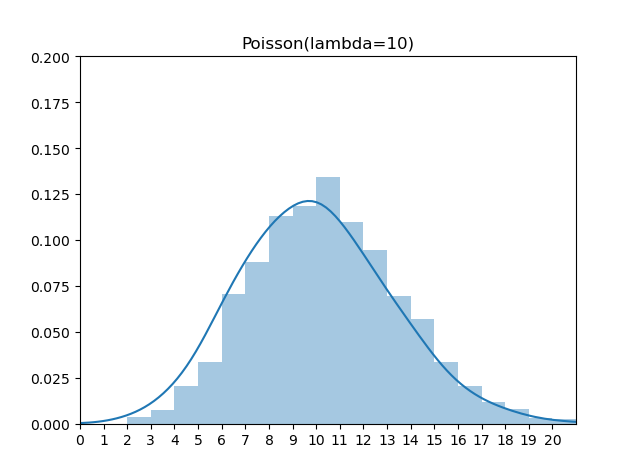
1 | import random |
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_poisson_inv.py
1 | from numpy.random import exponential |
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_poisson_from_exp.py
泊松分布

$ E_{1}, E_{2}, E_{3}, (1) $
\[ \mathbb{P}(K \geqslant k)=\mathbb{P}\left(E_{1}+\cdots+E_{k} \leqslant \lambda\right) \]
1 | from numpy.random import exponential |
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_poisson_from_exp.py
解读TRPO论文,一种深度强化学习和传统优化方法结合的方法

导读:本论文由Berkeley 的几位大神于2015年发表于 JMLR(Journal of Machine Learning Research)。深度强化学习算法例如DQN或者PG(Policy Gradient)都无法避免训练不稳定的问题:在训练过程中效果容易退化并且很难恢复。针对这个通病,TRPO采用了传统优化算法中的trust region方法,以保证每一步迭代能够获得效果提升,直至收敛到局部最优点。
本篇论文涉及到的知识点比较多,不仅建立在强化学习领域经典论文的结论:Kakade & Langford 于2002 年发表的 Approximately Optimal Approximate Reinforcement Learning 关于优化目标的近似目标和重要性采样,也涉及到传统优化方法 trust region 的建模和其具体的矩阵近似数值算法。读懂本论文,对于深度强化学习及其优化方法可以有比较深入的理解。本论文附录的证明部分由于更为深奥和冗长,在本文中不做具体讲解,但是也建议大家能够仔细研读。
阅读本论文需要注意的是,这里解读的版本是arxiv的版本,这个版本带有附录,不同于 JMLR的版本的是,arxiv版本中用reward函数而后者用cost函数,优化方向相反。
arxiv 下载链接为 https://arxiv.org/pdf/1502.05477.pdf
0. 论文框架
本论文解决的目标是希望每次迭代参数能保证提升效果,具体想法是利用优化领域的 trust region方法(中文可以翻译成置信域方法或信赖域方法),通过参数在trust region范围中去找到一定能提升的下一次迭代。
本论文框架如下
首先,引入Kakade & Langford 论文 Approximately Optimal Approximate Reinforcement Learning 中关于近似优化目标的结论。(论文第二部分)
基于 Kakade 论文中使用mixture policy保证每一步效果提升的方法,扩展到一般随机策略,引入策略分布的total variation divergence作为约束。(论文第三部分)
将total variation divergence约束替换成平均 KL divergence 约束,便于使用蒙特卡洛方法通过采样来生成每一步的具体优化问题。(论文第四,五部分)
给出解决优化问题的具体算法,将优化目标用first order来近似,约束项用second order 来近似,由于second order涉及到构造Hessian matrix,计算量巨大,论文给出了 conjugate gradient + Fisher information matrix的近似快速实现方案。(论文第六部分)
从理论角度指出,Kakade 在2002年提出的方法natrual policy gradient 和经典的policy gradient 都是TRPO的特别形式。(论文第七部分)
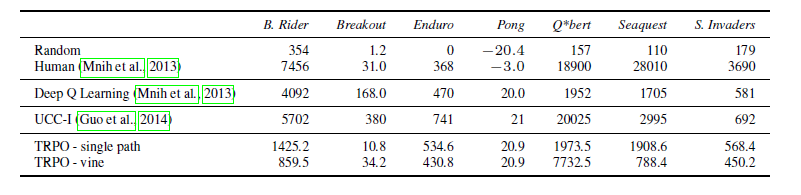
评价TRPO在两种强化学习模式下的最终效果,一种是MuJoCo模拟器中能得到真实状态的模式,一种是Atari游戏环境,即观察到的屏幕像素可以信息完全地表达潜在真实状态的模式。(论文第八部分)
本文下面的小结序号和论文小结序号相同,便于对照查阅。
1. 介绍
TRPO 第一次证明了最小化某种 surrogate 目标函数且采用non-trivial的步长,一定可以保证策略提升。进一步将此 surrogate 目标函数转换成trust region约束下的优化问题。TRPO是一种on-policy 的算法,因为每一步迭代,需要在新的策略下通过采样数据来构建具体优化问题。
2. 已有理论基础
第二部分主要回顾了 Kakade & Langford 于2002 年的论文 Approximately Optimal Approximate Reinforcement Learning 中的一系列结论。
先来定义几个重要概念的数学定义
\(\eta(\pi)\) 是策略 \(\pi\) 的目标,即discounted reward 和的期望。
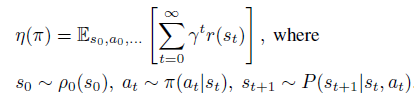
- 然后是策略的Q值和V值
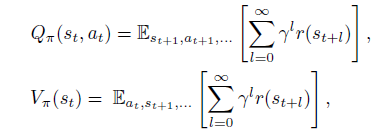
- 最后是策略的advantage函数
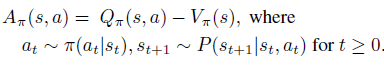
接着,开始引入 Kakade & Langford 论文结论,即下式(公式1)。
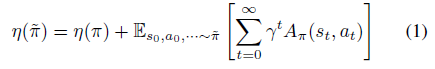
公式1表明,下一次迭代策略的目标可以分解成现有策略的目标 \(\eta(\pi)\) 和现有advantage 函数在新策略trajectory分布下的期望。
公式1可以很容易从trajectory分布转换成新策略在状态的访问频率,即公式2
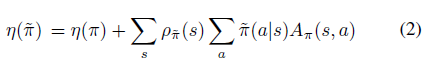
状态的访问频率或稳定状态分布定义成
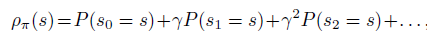
注意到公式2中状态的期望依然依赖于新策略 \(\rho_{\widetilde\pi}\) 的稳定状态分布,不方便实现。原因如下,期望形式有利于采样来解决问题,但是由于采样数据源于 on-policy \(\pi\) 而非 \({\widetilde\pi}\) ,因此无法直接采样未知的策略 \({\widetilde\pi}\)。
幸好,Kakade 论文中证明了,可以用 \(\rho_{\pi}\) 的代替 \(\rho_{\widetilde\pi}\) 并且证明了这种代替下的近似目标函数 \(L_{\pi}\) 是原来函数的一阶近似
\[ L_{\pi}(\widetilde\pi) \approx \eta(\widetilde\pi) \]
即满足
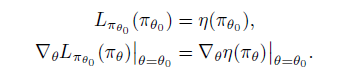
\(L_{\pi}\) 具体定义表达式为
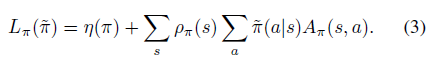
\(L_{\pi}(\widetilde\pi)\) 是一阶近似意味着在小范围区域中一定是可以得到提升的,但是范围是多大,是否能保证 \(\eta\) 的提升?Kakade的论文中不仅给出了通过mix新老策略的提升方式,还给出了这个方式对原目标 \(\eta\) 较 \(L_{\pi}(\widetilde\pi)\) 的提升下届。
策略更新规则如下
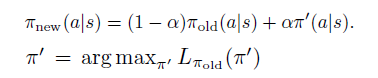
公式6为具体提升下届为
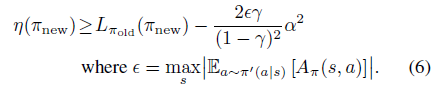
3. 扩展到随机策略
论文的这一部分将Kakade的mix policy update 扩展到一般的随机策略,同时依然保证每次迭代能得到目标提升。
首先,每次策略迭代必须不能和现有策略变化太大,因此,引入分布间常见的TV divergence,即 total variation divergence。
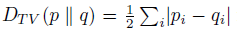
有了两个分布距离的定义,就可以定义两个策略的距离。离散状态下,一个策略是状态到动作分布的 map 或者 dict,因此,可以定义两个策略的距离为所有状态中最大的动作分布的 \(D_{TV}\),即
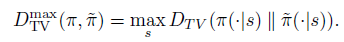
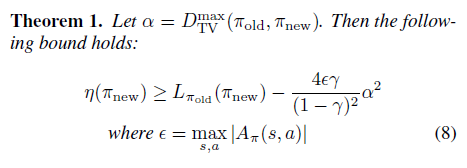
进一步将 TV divergence 转换成 KL divergence,转换成KL divergence 的目的是为了后续使用传统且成熟的 trust region 蒙特卡洛方法和 conjugate gradient 的优化近似解法。
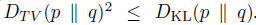
由于上面两种距离的大小关系,可以推导出用KL divergence表示的 \(\eta\) 较 \(L_{\pi}(\widetilde\pi)\) 的提升下届
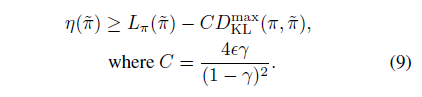
根据公式9,就可以形成初步的概念上的算法一,通过每一步形成无约束优化问题,同时保证每次迭代的 \(\pi_i\) 对应的 \(\eta\) 是递增的。

4. Trust Region Policy Optimization
看到这里已经不容易了,尽管算法一给出了一个解决方案,但是本论文的主角TRPO 还未登场。TRPO算法的作用依然是近似!
算法一对于下面的目标函数做优化,即每次找到下一个 \(\theta_i\) 最大化下式,\(\eta\) 每一步一定能得到提升。
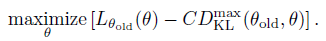
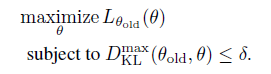
将 \(D^{max}_{KL}\) 放入约束项中符合trust region 这种传统优化解法。
关于 \(D^{max}_{KL}\) 约束,再补充两点
其定义是两个策略中所有状态中最大的动作分布的 \(D_{TV}\) ,因此它约束了所有状态下新老策略动作分布的KL散度,也就意味着有和状态数目相同数量的约束项,海量的约束项导致算法很难应用到实际中。
约束项的 trust region 不是参数 \(\theta\) 的空间,而是其KL散度的空间。
基于第一点,再次使用近似法,在约束项中用KL期望来代替各个状态下的KL散度,权重为on-policy 策略的分布 \(\rho(\theta_{old})\)
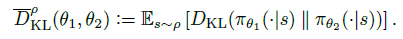
最终,得到TRPO在实际中的优化目标(12式):
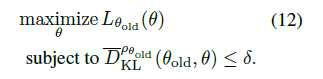
5. 用采样方法来Trust Region约束优化
论文第五部分,将TRPO优化目标12式改写成期望形式,引入两种蒙特卡洛方法 single path 和 vine 来采样。
具体来说,\(L_{\theta_{old}}\) 由两项组成 \[ L_{\theta_{old}} = \eta(\theta_{old}) + \sum_s \rho_{\theta_{old}}(s)\sum_a {\pi_{\theta}}(a |s) A_{\theta_{old}}(s,a) \]
第一项是常量,只需优化第二项,即优化问题等价为13式
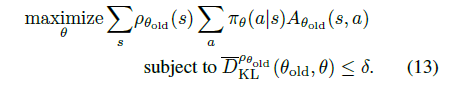
随后,为了可以适用非 on-policy \(\pi_{\theta_{old}}\) 的动作分布来任意采样,引入采样的动作分布 \(q(a|s)\),将13式中的 \(\sum_a\) 部分通过重要性采样改成以下形式:
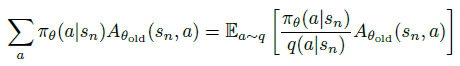
再将13式中的 \(\sum_s \rho(s)\) 改成期望形式 \(\mathbb{E}_{s \sim \rho}\) ,并将 \(A\) 改成 \(Q\) 值,得14式。
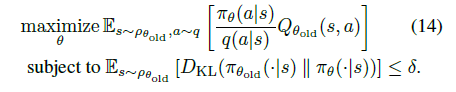
至此,我们得到trust region优化的期望形式:优化目标中期望的状态空间是基于 on-policy \(\pi_{\theta_{old}}\),动作空间是基于任意采样分布 \(q(a|s)\),优化约束中的期望是基于 on-policy \(\pi_{\theta_{old}}\)。
5.1 Single path采样
根据14式,single path 是最基本的的蒙特卡洛采样方法,和REINFORCE算法一样, 通过on-policy \(\pi_{\theta_{old}}\)生成采样的 trajectory数据: \(s_0, a_0, s_1, a_1, ..., a_{T-1}, s_{T}\),然后代入14式。注意,此时 \(q(a|s) = \pi_{\theta_{old}}(a|s)\),即用现有策略的动作分布直接代替采样分布。
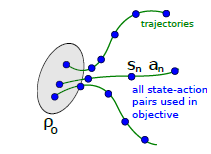
5.2 Vine 采样
虽然single path方法简单明了,但是有着online monte carlo方法固有的缺陷,即variance较大。Vine方法通过在一个状态多次采样来改善此缺陷。Vine的翻译是藤,寓意从一个状态多次出发来采样,如下图,\(s_n\) 状态下采样多个rollouts,很像植物的藤长出多分叉。当然,vine方法要求环境能restart 到某一状态,比如游戏环境通过save load返回先前的状态。
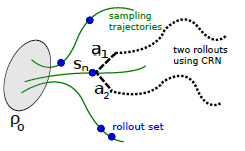
具体来说,vine 方法首先通过生成多个on-policy 的trajectories来确定一个状态集合 \(s_1, s_2, ..., s_N\)。对于状态集合的每一个状态 \(s_n\) 采样K个动作,服从 $ a_{n, k} q(s_{n}) $ 。接着,对于每一个 \((s_n, a_{n,k})\) 再去生成一次 rollout 来估计 \(\hat{Q}_{\theta_{i}}\left(s_{n}, a_{n, k}\right)\) 。试验证明,在连续动作空间问题中,\(q\left(\cdot \mid s_{n}\right)\) 直接使用 on-policy 可以取得不错效果,在离散空间问题中,使用uniform分布效果更好。
6. 转换成具体优化问题
再回顾一下现在的进度,12式定义了优化目标,约束项是KL divergence空间的trust region 形式。14式改写成了等价的期望形式,通过两种蒙特卡洛方法生成 state-action 数据集,可以代入14式得到每一步的具体数值的优化问题。论文这一部分简单叙述了如何高效但近似的解此类问题,详细的一些步骤在附录中阐述。我们把相关解读都放在下一节。
7. 和已有理论的联系
7.1 简化成 Natural Policy Gradient
再回到12式,即约束项是KL divergence空间的trust region 形式
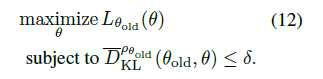
对于这种形式的优化问题,一般的做法是通过对优化目标做一阶函数近似,即 \[ L_{\theta_{old}}(\theta) \approx L_{\theta_{old}}\left(\theta_{old}\right)+g^{T}\left(\theta-\theta_{old}\right) \]
\[ \left.g \doteq \nabla_{\theta} L_{\theta_{old}}(\theta)\right|_{\theta_{old}} \]
并对约束函数做二阶函数近似,因为约束函数在 \(\theta_{old}\) 点取到极值,因此一阶导为0。 \[ \bar{D}_{K L}\left(\theta \| \theta_{old}\right) \approx \frac{1}{2}\left(\theta-\theta_{old}\right)^{T} H\left(\theta-\theta_{old}\right) \]
\[ \left.H \doteq \nabla_{\theta}^{2} \bar{D}_{K L}\left(\theta \| \theta_{old}\right)\right|_{\theta_{old}} \]
12式的优化目标可以转换成17式
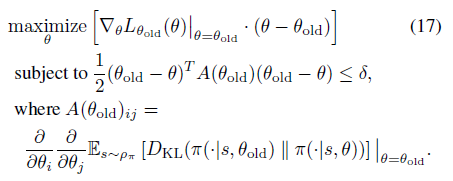
对应参数迭代更新公式如下
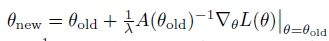
这个方法便是Kakade在2002年发表的 natrual policy gradient 论文。
7.2 简化成 Policy Gradient
注意,\(L_{\theta_{old}}\)的一阶近似的梯度 \[ \left.\nabla_{\theta} L_{\theta_{\text {old }}}(\theta)\right|_{\theta=\theta_{\text {old }}} \cdot\left(\theta-\theta_{\text {old }}\right) \]
即PG定理 \[ \frac{\partial \rho}{\partial \theta}=\sum_{s} d^{\pi}(s) \sum_{a} \frac{\partial \pi(s, a)}{\partial \theta} Q^{\pi}(s, a) \]
因此,PG定理等价于\(L_{\theta_{old}}\)的一阶近似的梯度在\(\theta\) 空间 \(l_2\) 约束下的优化问题,即18式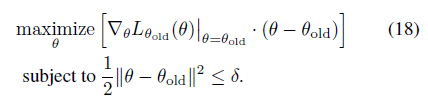
7.3 近似数值解法
这里简单描述关于17式及其参数更新规则中的大矩阵数值计算近似方式。
$ {D}_{}^{} $ 二阶近似中的 \(A\) 是 Hessian 方形矩阵,维度为 \(\theta\) 个数的平方。
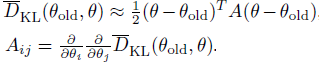
直接构建 \(A\) 矩阵或者其逆矩阵 \(A^{-1}\)都是计算量巨大的, 注\(A^{-1}\)出现在natural policy update \(\theta\) 更新公式中,\(A^{-1} \nabla_{\theta} L(\theta)\) 。
一种方法是通过构建Fisher Information Matrix,引入期望形式便于采样 \[ \mathbf{A}=E_{\pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}(\mathbf{a} \mid \mathbf{s}) \nabla_{\theta} \log \pi_{\theta}(\mathbf{a} \mid \mathbf{s})^{T}\right] \] 另一种方式是使用conjugate gradient 方法,通过矩阵乘以向量快速计算法迭代逼近 \(A^{-1} \nabla_{\theta} L(\theta)\)。
8. 试验结果
在两种强化学习模式下,比较TRPO和其他模型的效果。模式一是在MuJoCo模拟器中,这种环境下能得到真实状态的情况。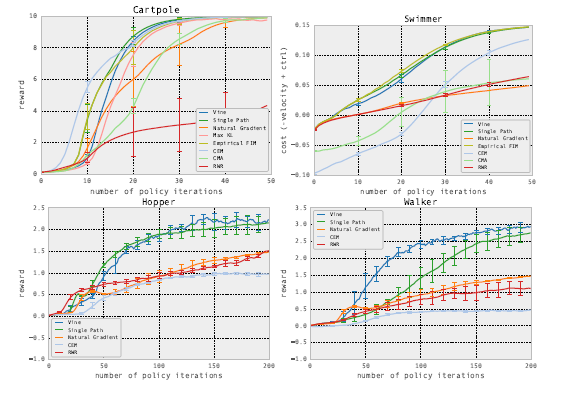
另一种模式是完全信息下的Atari游戏环境,这种环境下观察到的屏幕像素可以信息完全地表达潜在真实状态。
解读深度强化学习基石论文:函数近似的策略梯度方法

导读:这篇式1999 年Richard Sutton 在强化学习领域中的经典论文,论文证明了策略梯度定理和在用函数近似 Q 值时策略梯度定理依然成立,本文奠定了后续以深度强化学习策略梯度方法的基石。理解熟悉本论文对 Policy Gradient,Actor Critic 方法有很好的指导意义。
论文分成四部分。第一部分指出策略梯度在两种期望回报定义下都成立(定理一)。第二部分提出,如果 \(Q^{\pi}\) 被函数 \(f_w\) 近似时且满足兼容(compatible)条件,以 \(f_w\) 替换策略梯度中的 \(Q^{\pi}\)公式也成立(定理二)。第三部分举Gibbs分布的策略为例,如何应用 \(Q^{\pi}\)近似函数来实现策略梯度算法。第四部分证明了近似函数的策略梯度迭代法一定能收敛到局部最优解。附录部分证明了两种定义下的策略梯度定理。
1. 策略梯度定理
对于Agent和环境而言,可以分成episode和non-episode,后者的时间步骤可以趋近于无穷大,但一般都可以适用两种期望回报定义。一种是单步平均reward ,另一种是指定唯一开始状态并对trajectory求 \(\gamma\)-discounted 之和,称为开始状态定义。两种定义都考虑到了reward的sum会趋近于无穷大,通过不同的方式降低了此问题的概率。
A. 平均reward定义
目标函数 \(\rho(\pi)\) 定义成单步的平均reward,这种情况下等价于稳定状态分布下期望值。
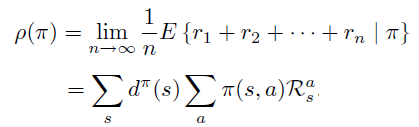
稳定状态分布定义成无限次数后状态的分布。
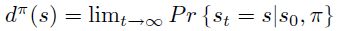
此时,\(Q^{\pi}\) 定义为无限步的reward sum 减去累积的单步平均 reward \(\rho(\pi)\),这里减去\(\rho(\pi)\)是为了一定程度防止 \(Q^{\pi}\)没有上界。
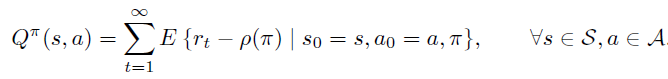
B. 开始状态定义
在开始状态定义方式中,某指定状态\(s_0\)作为起始状态,\(\rho(\pi)\) 的定义为 trajectory 的期望回报,注意由于时间步骤 t 趋近于无穷大,必须要乘以discount 系数 \(\gamma < 1\) 保证期望不会趋近无穷大。
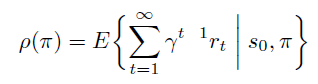
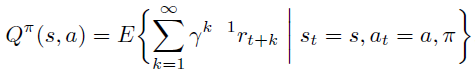
\(d^{\pi}\) 依然为无限次数后状态的稳定分布。
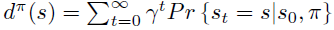
策略梯度定理
论文指出上述两种定义都满足策略梯度定理,即目标 \(\rho\) 对于参数 \(\theta\) 的偏导不依赖于 \(d^{\pi}\) 对于 \(\theta\) 偏导,仅取决
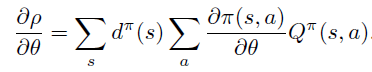
关于策略梯度定理的一些综述,可以参考。
论文中还提到策略梯度定理公式和经典的William REINFORCE算法之间的联系。REINFORCE算法即策略梯度的蒙特卡洛实现。
联系如下:
首先,根据策略梯度定理,如果状态 s 是通过 \(\pi\) 采样得到,则下式是$$ 的无偏估计。注意,这里action的summation和 \(\pi\) 是无关的。
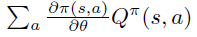
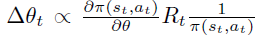
2. 函数近似的策略梯度
论文第二部分,进一步引入 \(Q_{\pi}\) 的近似函数 \(f_w\): $ $。
如果我们有\(Q_{\pi}(s_t, a_t)\)的无偏估计,例如 \(R_t\),很自然,可以让 \(\partial f_w \over \partial w\) 通过最小化 \(R_t\) 和 \(f_w\)之间的差距来计算。
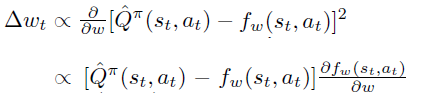
当拟合过程收敛到局部最优时,策略梯度定理中右边项对于 \(w\) 求导为0,可得(3)式。
.png)
至此,引出策略梯度定理的延续,即定理2:当 \(f_w\) 满足(3)式同时满足(4)式(称为compatible条件时),可以用 \(f_w(s, a)\)替换原策略梯度中的 \(Q_{\pi}(s,a)\)

3. 一个应用示例
假设一个策略用features的线性组合后的 Gibbs分布来生成,即:
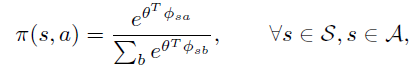
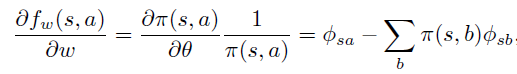
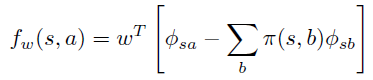
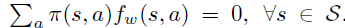
上式和advantage 函数 \(A^{\pi}(s, a)\) 定义一致,因此可以认为 \(f_w\) 的意义是 \(A^{\pi}\) 的近似。
\(A^{\pi}\)具体定义如下
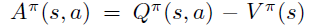
4. 函数近似的策略梯度收敛性证明
这一部分证明了在满足一定条件后,\(\theta\) 可以收敛到局部最优点。
条件为
- Compatible 条件,公式(4)
- 任意两个 \(\partial \pi \over \partial \theta\) 偏导是有限的,即
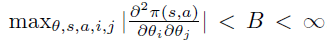
- 步长数列满足如下条件
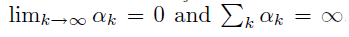
环境的 reward 是有限的
此时,当 \(w_k\) 和 \(\theta_k\) 按如下方式迭代一定能收敛到局部最优。
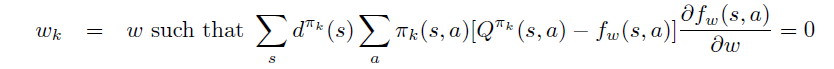
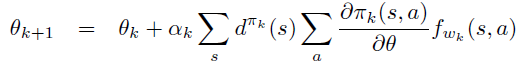
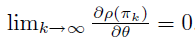
5. 策略梯度定理的两种情况下的证明
下面简单分解策略梯度的证明步骤。
A. 平均reward 定义下的证明
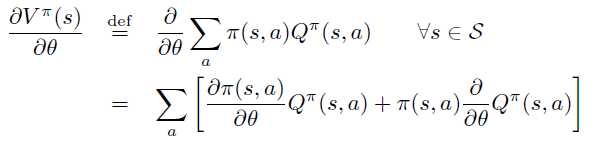
根据定义,将 \(\theta\) 导数放入求和号中,并分别对乘积中的每项求导。
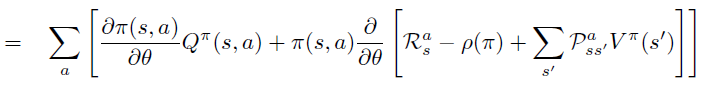
将\(Q_{\pi}\)的定义代入第二项 \(Q^{\pi}\) 对 \(\theta\) 求偏导中,引入环境reward 随机变量 \(R^a_s\),环境dynamics \(P\) 和 \(\rho(\pi)\)
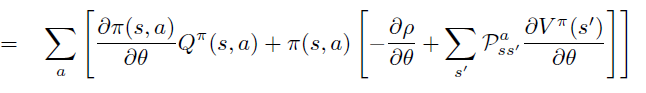
\(\theta\) 偏导进一步移入,\(R^a_s\), \(P\) 不依赖于\(\theta\)。
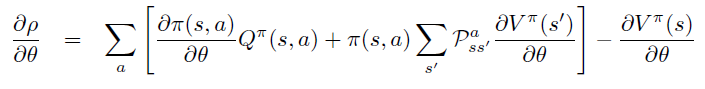
\(\rho(\pi)\) 对于 \(\theta\) 偏导整理到等式左边
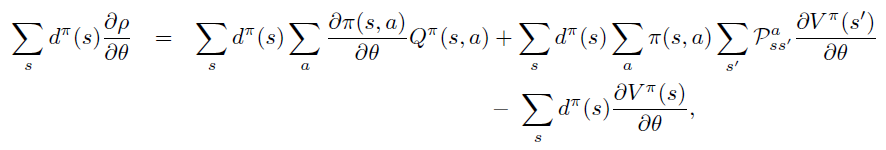
两边同时乘以 \(\sum d^{\pi}\)
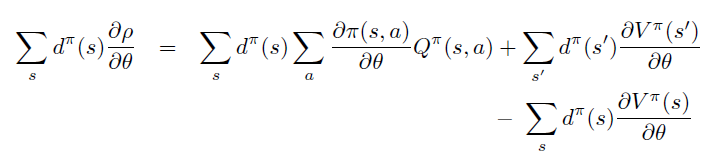
由于 \(d^{\pi}\) 是状态在 \(\pi\) 下的平稳分布,\(\sum \pi \sum P\) 项表示 agent 主观 \(\pi\) 和环境客观 \(P\) 对于状态分布的影响,因此可以直接去除。
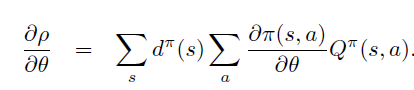
整理证得。
B. Start-state 定义下的证明
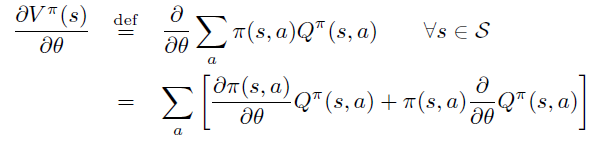
根据定义,将 \(\theta\) 导数放入求和号中,并分别对乘积中的每项求导。
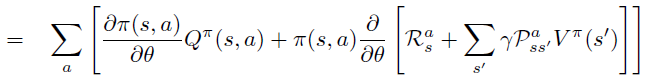
将\(Q_{\pi}\)的定义代入第二项 \(Q^{\pi}\) 对 \(\theta\) 求偏导中,引入环境reward 随机变量 \(R^a_s\),环境dynamics \(P\)
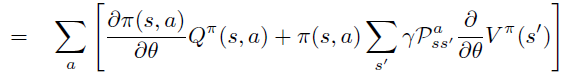
\(\theta\) 偏导进一步移入,\(R^a_s\), \(P\) 不依赖于\(\theta\)。注意,此式表示从状态 \(s\) 出发一步之后的能到达的所有 \(s^{\prime}\) ,将次式反复unroll \(V^{\pi}\) 成 \(Q^{\pi}\) 之后得到
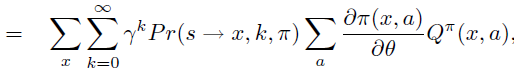
\(\operatorname{Pr}(s \rightarrow x, k, \pi)\) 表示 k 步后 状态 s 能到达的所有状态 x
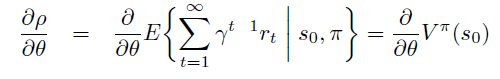
根据定义,\(\rho = V^{\pi}(s_0)\)
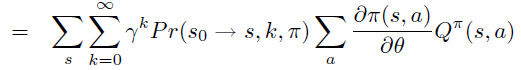
将 \(V^{\pi}(s_0)\) 替换成unroll 成 \(Q^{\pi}\) 的表达式
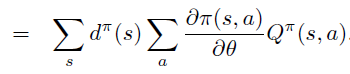
\(\operatorname{Pr}(s \rightarrow x, k, \pi)\) 即 \(d^{\pi}\)
深度强化学习之:Policy Gradient Theorem 一些理解
Policy gradient 定理作为现代深度强化学习的基石,同时也是actor-critic的基础,重要性不言而喻。但是它的推导和理解不是那么浅显,不同的资料中又有着众多形式,不禁令人困惑。本篇文章MyEncyclopedia试图总结众多资料背后的一些相通的地方,并写下自己的一些学习理解心得。
引入 Policy Gradient
Policy gradient 引入的目的是若我们将策略 \(\pi_{\theta}\) 的参数 \(\theta\) 直接和一个标量 \(J\) 直接联系在一起的话,就能够利用目前最流行的深度学习自动求导的方法,迭代地去找到 \(\theta^*\) 来最大化 \(J\):\[ \theta^{\star}=\arg \max _{\theta} J(\theta) \]
\[ {\theta}_{t+1} \doteq {\theta}_{t}+\alpha \nabla J(\theta) \]
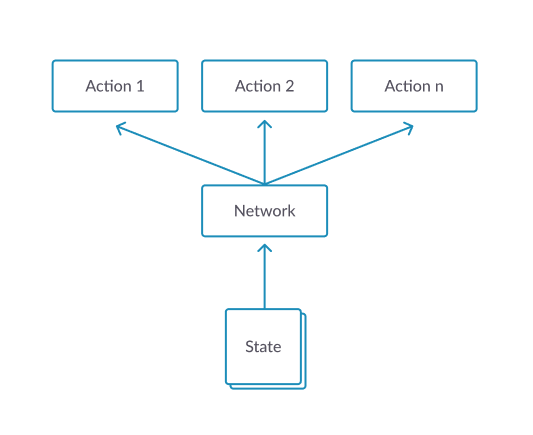
那么问题来了,首先一个如何定义 \(J(\theta)\),其次,如何求出或者估计 $ J()$。
第一个问题比较直白,用value function或者广义的expected return都可以。
这里列举一些常见的定义。对于episodic 并且初始都是 \(s_0\)状态的情况,直接定义成v值,即Sutton教程中的episodic情况下的定义
\[ J(\boldsymbol{\theta}) \doteq v_{\pi_{\boldsymbol{\theta}}}\left(s_{0}\right) \quad \quad \text{(1.1)} \]
\[ \begin{aligned} J(\theta) &= \sum_{s \in \mathcal{S}} d^{\pi}(s) V^{\pi}(s) \\ &=\sum_{s \in \mathcal{S}} d^{\pi}(s) \sum_{a \in \mathcal{A}} \pi_{\theta}(a \mid s) Q^{\pi}(s, a) \end{aligned} \quad \quad \text{(1.2)} \]
其中,状态平稳分布 \(d^{\pi}(s)\) 定义为
\[ d^{\pi}(s)=\lim _{t \rightarrow \infty} P\left(s_{t}=s \mid s_{0}, \pi_{\theta}\right) \]
\[ J(\boldsymbol{\theta}) \doteq E_{\tau \sim p_{\theta}(\tau)}\left[\sum_{t} r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right] \quad \quad \text{(1.3)} \]
即$ $ 是一次trajectory,服从以 \(\theta\) 作为参数的随机变量
\[ \tau \sim p_{\theta}\left(\mathbf{s}_{1}, \mathbf{a}_{1}, \ldots, \mathbf{s}_{T}, \mathbf{a}_{T}\right) \]
\(J(\theta)\) 对于所有的可能的 \(\tau\) 求 expected return。这种视角下对于finite 和 infinite horizon来说也有变形。
Infinite horizon 情况下,通过 \((s, a)\) 的marginal distribution来计算\[ J(\boldsymbol{\theta}) \doteq E_{(\mathbf{s}, \mathbf{a}) \sim p_{\theta}(\mathbf{s}, \mathbf{a})}[r(\mathbf{s}, \mathbf{a})] \quad \quad \text{(1.4)} \]
\[ J(\boldsymbol{\theta}) \doteq \sum_{t=1}^{T} E_{\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right) \sim p_{\theta}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)} \quad \quad \text{(1.5)} \]
\[ p\left(s^{\prime}, r \mid s, a\right) = \operatorname{Pr}\left\{S_{t}=s^{\prime}, R_{t}=r \mid S_{t-1}=s, A_{t-1}=a\right\} \]
当环境dynamics未知时,如何再去求 $ J()$ 呢。还有就是如果涉及到状态的分布也是取决于环境dynamics的,计算 $ J()$ 也面临同样的问题。
幸好,policy gradient定理完美的解答了上述问题。我们先来看看它的表述内容。
Policy Gradient Theorem
策略梯度定理证明了,无论定义何种 \(J(\theta)\) ,策略梯度等比于下式,其中 \(\mu(s)\) 为 \(\pi_{\theta}\) 下的状态分布。等比系数在episodic情况下为episode的平均长度,在infinite horizon情况下为1。\[ \nabla J(\boldsymbol{\theta}) \propto \sum_{s} \mu(s) \sum_{a} q_{\pi}(s, a) \nabla \pi(a \mid s, \boldsymbol{\theta}) \quad \quad \text{(2.1)} \]
\[ \nabla J(\boldsymbol{\theta}) =\mathbb{E}_{\pi}\left[\sum_{a} q_{\pi}\left(S_{t}, a\right) \nabla \pi\left(a \mid S_{t}, \boldsymbol{\theta}\right)\right] \quad \quad \text{(2.2)} \]
Policy Gradient 定理的伟大之处在于等式右边并没有 \(d^{\pi}(s)\),或者环境transition model \(p\left(s^{\prime}, r \mid s, a\right)\)!同时,等式右边变换成了最利于统计采样的期望形式,因为期望可以通过样本的平均来估算。
但是,这里必须注意的是action space的期望并不是基于 $(a S_{t}, ) $ 的权重的,因此,继续改变形式,引入 action space的 on policy 权重 $(a S_{t}, ) $ ,得到 2.3式。
\[ \nabla J(\boldsymbol{\theta})=\mathbb{E}_{\pi}\left[\sum_{a} \pi\left(a \mid S_{t}, \boldsymbol{\theta}\right) q_{\pi}\left(S_{t}, a\right) \frac{\nabla \pi\left(a \mid S_{t}, \boldsymbol{\theta}\right)}{\pi\left(a \mid S_{t}, \boldsymbol{\theta}\right)}\right] \quad \quad \text{(2.3)} \]
\[ \nabla J(\boldsymbol{\theta})==\mathbb{E}_{\pi}\left[q_{\pi}\left(S_{t}, A_{t}\right) \frac{\nabla \pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}\right)}{\pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}\right)}\right] \quad \quad \text{(2.4)} \]
将 \(q_{\pi}\)替换成 \(G_t\),由于
\[ \mathbb{E}_{\pi}[G_{t} \mid S_{t}, A_{t}]= q_{\pi}\left(S_{t}, A_{t}\right) \]
得到2.5式
\[ \nabla J(\boldsymbol{\theta})==\mathbb{E}_{\pi}\left[G_{t} \frac{\nabla \pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}\right)}{\pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}\right)}\right] \quad \quad \text{(2.5)} \]
\[ \nabla J(\boldsymbol{\theta}) \approx G_{t} \frac{\nabla \pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}\right)}{\pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}\right)} \quad \quad \text{(2.6)} \]
\[ \boldsymbol{\theta}_{t+1} \doteq \boldsymbol{\theta}_{t}+\alpha G_{t} \frac{\nabla \pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)}{\pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)} \quad \quad \text{(2.7)} \]

Policy Gradient Theorem - Trajectory Form
Trajectory 形式的策略梯度定理也很常见,这里也总结一下,回顾 1.3 式 \(J(\theta)\)的定义\[ J(\boldsymbol{\theta}) \doteq E_{\tau \sim p_{\theta}(\tau)}\left[\sum_{t} r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right] \quad \quad \text{(1.3)} \]
\[ \nabla_{\theta} J\left(\pi_{\theta}\right)=\underset{\tau \sim \pi_{\theta}}{\mathrm{E}}\left[\sum_{t=0}^{T} \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right) R(\tau)\right] \quad \quad \text{(3.1)} \]
\[ \hat{R}_{t} \doteq \sum_{t^{\prime}=t}^{T} R\left(s_{t^{\prime}}, a_{t^{\prime}}, s_{t^{\prime}+1}\right) \]
\[ \nabla_{\theta} J\left(\pi_{\theta}\right)=\underset{\tau \sim \pi_{\theta}}{\mathrm{E}}\left[\sum_{t=0}^{T} \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right) \hat{R}_{t} \right] \quad \quad \text{(3.2)} \]
\[ \nabla_{\theta} \log \pi_{\theta}(a)=\frac{\nabla_{\theta} \pi_{\theta}}{\pi_{\theta}} \quad \quad \text{(3.3)} \]
和监督学习的联系
Policy Gradient中的 \(\nabla_{\theta} \log \pi\) 广泛存在在机器学习范畴中,被称为 score function gradient estimator。RL 在supervised learning settings 中有 imitation learning,即通过专家的较优stochastic policy \(\pi_{\theta}(a|s)\) 收集数据集
\[ \{(s_1, a^{*}_1), (s_2, a^{*}_2), ...\} \]
\[ \theta^{*}=\operatorname{argmax}_{\theta} \sum_{n} \log \pi_{\theta}\left(a_{n}^{*} \mid s_{n}\right) \quad \quad \text{(4.1)} \]
\[ \theta_{n+1} \leftarrow \theta_{n}+\alpha_{n} \nabla_{\theta} \log \pi_{\theta}\left(a_{n}^{*} \mid s_{n}\right) \quad \quad \text{(4.2)} \]
对照Policy Graident RL,on-policy \(\pi_{\theta}(a|s)\) 产生数据集
\[ \{(s_1, a_1, r_1), (s_2, a_2, r_2), ...\} \]
目标是最大化on-policy \(\pi_{\theta}\) 分布下的expected return
\[ \theta^{*}=\operatorname{argmax}_{\theta} \sum_{n} R(\tau_{n}) \]
\[ \theta_{n+1} \leftarrow \theta_{n}+\alpha_{n} G_{n} \nabla_{\theta} \log \pi_{\theta}\left(a_{n} \mid s_{n}\right) \quad \quad \text{(4.3)} \]
对比 4.3 和 4.2,发现此时4.3中只多了一个权重系数 \(G_n\)。
关于 $G_{n} {} {}(a_{n} s_{n}) $ 或者 \(G_{t} \frac{\nabla \pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)}{\pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)}\) 有一些深入的理解。
首先policy gradient RL 不像supervised imitation learning直接有label 作为signal,PG RL必须通过采样不同的action获得reward或者return作为signal,即1.4式中的\[ E_{(\mathbf{s}, \mathbf{a}) \sim p_{\theta}(\mathbf{s}, \mathbf{a})}[r(\mathbf{s}, \mathbf{a})] \quad \quad \text{(5.1)} \]
\[ E_{x \sim p(x \mid \theta)}[f(x)] \quad \quad \text{(5.2)} \]
\[ \begin{aligned} \nabla_{\theta} E_{x}[f(x)] &=\nabla_{\theta} \sum_{x} p(x) f(x) \\ &=\sum_{x} \nabla_{\theta} p(x) f(x) \\ &=\sum_{x} p(x) \frac{\nabla_{\theta} p(x)}{p(x)} f(x) \\ &=\sum_{x} p(x) \nabla_{\theta} \log p(x) f(x) \\ &=E_{x}\left[f(x) \nabla_{\theta} \log p(x)\right] \end{aligned} \quad \quad \text{(5.3)} \]
Policy Gradient 工作的机制大致如下
首先,根据现有的 on-policy \(\pi_{\theta}\) 采样出一些动作 action 产生trajectories,这些trajectories最终得到反馈 \(R(\tau)\)
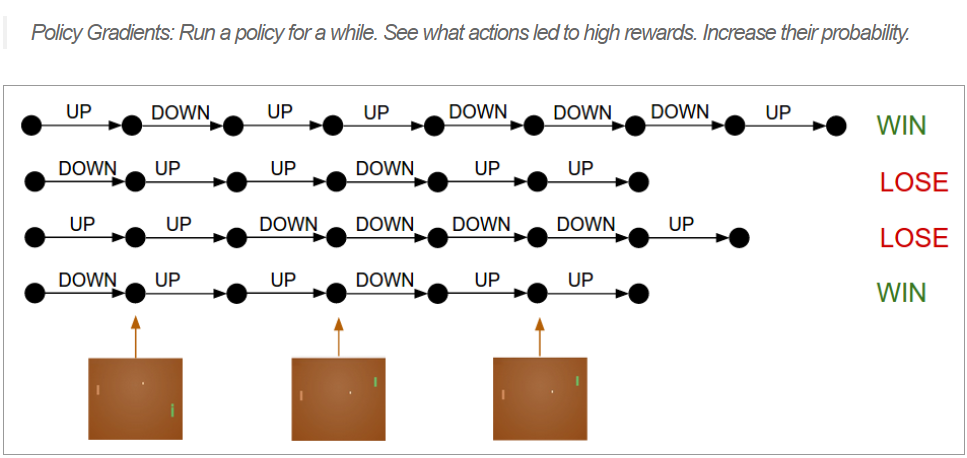
\[ R(s,a) \nabla \pi_{\theta_{t}}(a \mid s) \approx \nabla \pi_{\theta_{t}}(a^{*} \mid s) \]
最后,由于采样到的action分布服从于\(a \sim \pi_{\theta}(a)\) ,除掉 \(\pi_{\theta}\) :
\(G_{t} \frac{\nabla \pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)}{\pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)}\)
此时,采样的均值可以去无偏估计2.2式中的Expectation。
\[ \sum_N G_{t} \frac{\nabla \pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)}{\pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)} \]
\[ =\mathbb{E}_{\pi}\left[\sum_{a} q_{\pi}\left(S_{t}, a\right) \nabla \pi\left(a \mid S_{t}, \boldsymbol{\theta}\right)\right] \]
深度强化学习之:DQN训练超级玛丽闯关
上一期 MyEncyclopedia公众号文章 从Q-Learning 演化到 DQN,我们从原理上讲解了DQN算法,这一期,让我们通过代码来实现任天堂游戏机中经典的超级玛丽的自动通关吧。本文所有代码在 https://github.com/MyEncyclopedia/reinforcement-learning-2nd/tree/master/super_mario。
DQN 算法回顾
上期详细讲解了DQN中的两个重要的技术:Target Network 和 Experience Replay,正是有了它们才使得 Deep Q Network在实战中容易收敛,以下是Deepmind 发表在Nature 的 Human-level control through deep reinforcement learning 的完整算法流程。

超级玛丽 NES OpenAI 环境
安装基于OpenAI gym的超级玛丽环境执行下面的 pip 命令即可。
1 | pip install gym-super-mario-bros |
我们先来看一下游戏环境的输入和输出。下面代码采用随机的action来和游戏交互。有了 组合游戏系列3: 井字棋、五子棋的OpenAI Gym GUI环境 对于OpenAI Gym 接口的介绍,现在对于其基本的交互步骤已经不陌生了。
1 | import gym_super_mario_bros |
游戏render效果如下
。。。
注意我们在游戏环境初始化的时候用了参数 RIGHT_ONLY,它定义成五种动作的list,表示仅使用右键的一些组合,适用于快速训练来完成Mario第一关。
1 | RIGHT_ONLY = [ |
观察一些 info 输出内容,coins表示金币获得数量,flag_get 表示是否取得最后的旗子,time 剩余时间,以及 Mario 大小状态和所在的 x,y位置。
1 | { |
游戏图像处理
Deep Reinforcement Learning 一般是 end-to-end learning,意味着游戏的 screen image 作为observation直接视为真实状态,喂给神经网络训练。于此相反的另一种做法是,通过游戏环境拿到内部状态,例如所有相关物品的位置和属性作为模型输入。这两种方式的区别有两点。第一点,用观察到的屏幕像素代替真正的状态 s,在partially observable 的环境时可能因为 non-stationarity 导致无法很好的工作,而拿内部状态利用了额外的作弊信息,在partially observable环境中也可以工作。第二点,第一种方式屏幕像素维度比较高,输入数据量大,需要神经网络的大量训练拟合,第二种方式,内部真实状态往往维度低得多,训练起来很快,但缺点是因为除了内部状态往往还需要游戏相关规则作为输入,因此generalization能力不如前者强。
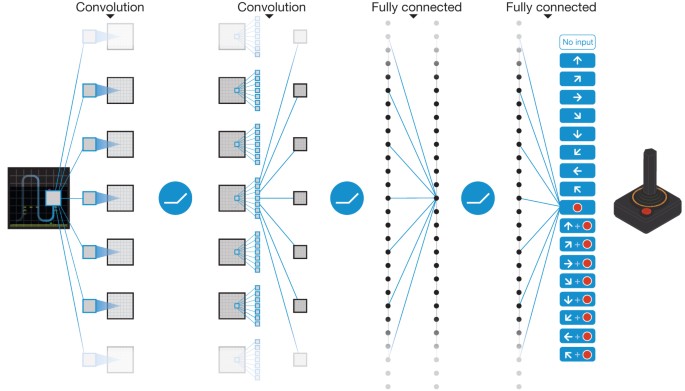
这里,我们当然采样屏幕像素的 end-to-end 方式了,自然首要任务是将游戏帧图像有效处理。超级玛丽游戏环境的屏幕输出是 (240, 256, 3) shape的 numpy array,通过下面一系列的转换,尽可能的在不影响训练效果的情况下减小采样到的数据量。
MaxAndSkipFrameWrapper:每4个frame连在一起,采取同样的动作,降低frame数量。
FrameDownsampleWrapper:将原始的 (240, 256, 3) down sample 到 (84, 84, 1)
ImageToPyTorchWrapper:转换成适合 pytorch 的 (1, 84, 84) shape
FrameBufferWrapper:保存最后4次屏幕采样
NormalizeFloats:Normalize 成 [0., 1.0] 的浮点值
1 | def wrap_environment(env_name: str, action_space: list) -> Wrapper: |
CNN 模型
模型比较简单,三个卷积层后做 softmax输出,输出维度数为离散动作数。act() 采用了epsilon-greedy 模式,即在epsilon小概率时采取随机动作来 explore,大于epsilon时采取估计的最可能动作来 exploit。
1 | class DQNModel(nn.Module): |
Experience Replay 缓存
实现采用了 Pytorch CartPole DQN 的官方代码,本质是一个最大为 capacity 的 list 保存采样的 (s, a, r, s', is_done) 五元组。
1 | Transition = namedtuple('Transition', ('state', 'action', 'reward', 'next_state', 'done')) |
DQNAgent
我们将 DQN 的逻辑封装在 DQNAgent 类中。DQNAgent 成员变量包括两个 DQNModel,一个ReplayMemory。
train() 方法中会每隔一定时间将 Target Network 的参数同步成现行Network的参数。在td_loss_backprop()方法中采样 ReplayMemory 中的五元组,通过minimize TD error方式来改进现行 Network 参数 \(\theta\)。Loss函数为:
\[ L\left(\theta_{i}\right)=\mathbb{E}_{\left(s, a, r, s^{\prime}\right) \sim \mathrm{U}(D)}\left[\left(r+\gamma \max _{a^{\prime}} Q_{target}\left(s^{\prime}, a^{\prime} ; \theta_{i}^{-}\right)-Q\left(s, a ; \theta_{i}\right)\right)^{2}\right] \]
1 | class DQNAgent(): |
外层 Training 代码
最后是外层调用代码,基本和以前文章一样。
1 | def train(env, args, agent): |
TSP问题从DP算法到深度学习4:概率最大状态序列算法
本篇是TSP问题从DP算法到深度学习系列第四篇,这一篇我们会详细举例并比较在 seq-to-seq 或者Markov Chain中的一些常见的搜索概率最大的状态序列的算法。这些方法在深度学习的seq-to-seq 中被用作decoding。在第五篇中,我们使用强化学习时也会使用了本篇中讲到的方法。
第四篇: 搜寻最有可能路径:Viterbi算法和其他
第五篇: 深度强化学习无监督算法的 Pytorch实现
马尔科夫链问题
在 seq-to-seq 问题中,我们经常会遇到需要从现有模型中找概率最大的可能状态序列。这类问题在机器学习算法和控制领域广泛存在,抽象出来可以表达成马尔可夫链模型:给定初始状态的分布和系统的状态转移方程(称为系统动力,dynamics),找寻最有可能的状态序列。
举个例子,假设系统有 \(n\) 个状态,初始状态由 $s_0 = [0.35, 0.25, 0.4] $ 指定,表示初始时三种状态的分布为 0.35,0.25和0.4。
状态转移矩阵由 \(T\) 表达,其中 $ T[i][j]$ 表示从状态 \(i\) 到状态 \(j\) 的概率。注意下面的矩阵 \(T\) 每行的和为 1.0,对应了从任意状态出发,下一时刻的所有可能转移概率和为1。 \[ T= \begin{matrix} & \begin{matrix}0&1&2\end{matrix} \\\\ \begin{matrix}0\\\\1\\\\2\end{matrix} & \begin{bmatrix}0.3&0.6&0.1\\\\0.4&0.2&0.4\\\\0.3&0.3&0.4\end{bmatrix}\\\\ \end{matrix} \]
至此,系统的所有参数都定下来了。接下去的各个时刻的状态分布可以通过矩阵乘法来算得。比如,记\(s_1\) 为 \(t_1\) 时刻状态分布,计算方法为 \(s_0\) 乘以 \(T\),动画如下:
\(s_1\) 数值计算结果如下。
\[ s_1 = \begin{bmatrix}0.35& 0.25& 0.4\end{bmatrix} \begin{matrix} \begin{bmatrix}0.3&0.6&0.1\\\\0.4&0.2&0.4\\\\0.3&0.3&0.4\end{bmatrix}\\\\ \end{matrix} = \begin{bmatrix}0.325& 0.35& 0.255\end{bmatrix} \] 矩阵左乘行向量可以理解为矩阵每一行的线性组合,直觉上理解为下一时刻的状态分布是上一时刻初始状态分布乘以转移关系的线性组合。 \[ \begin{bmatrix}0.35& 0.25& 0.4\end{bmatrix} \begin{matrix} \begin{bmatrix}0.3&0.6&0.1\\\\0.4&0.2&0.4\\\\0.3&0.3&0.4\end{bmatrix}\\\\ \end{matrix} = 0.35 \times \begin{bmatrix}0.35& 0.6& 0.1\end{bmatrix} + 0.25 \times \begin{bmatrix}0.4& 0.2& 0.4\end{bmatrix} + 0.4 \times \begin{bmatrix}0.3& 0.3& 0.4\end{bmatrix} \] 同样的,后面每一个时刻都可以由上一个状态分布向量乘以 \(T\),当然这里我们假设每个时刻的转移矩阵是不变的。当然,问题也可以是每个时刻都有不同的转移矩阵来定义,例如深度学习 seq-to-seq 模型。当然,这个设定的变化不会影响搜索最可能状态序列的算法。出于简单考虑,本篇中我们假定所有时刻的状态转移矩阵都是 \(T\)。
下面我们通过多种算法来找出由上述参数定义的系统中前三个时刻的最有可能序列,即概率最大的 \(s_0 \rightarrow s_1 \rightarrow s_2\)。
令 \(L\) 是阶段数,\(N\) 是每个阶段的状态数,则我们的例子中 \(L=N=3\) 。并且,总共有 \(N^L\) 种不同的路径。
穷竭搜索
若给定一条路径,计算特定路径的概率是很直接的,例如,若给定路径为 \(2(s_0) \rightarrow 1(s_1) \rightarrow 2(s_2)\),则这条路径的概率为
\[ p(2 \rightarrow 1 \rightarrow 2) = s_0[2] \times T[2][1] \times T[1][2] = 0.4 \times 0.3 \times 0.4 = 0.048 \]
因此,我们可以通过枚举所有 \(N^L\) 条路径并计算每条路径的概率来找到最有可能的状态序列。
下面是Python 3的穷竭搜索代码,输出为最有可能的概率及其路径。样例问题的输出为 0.084 和状态序列 \(0 \rightarrow 1 \rightarrow 2\)。
1 | def search_brute_force(initial: List, transition: List, L: int) -> Tuple[float, Tuple]: |
贪心搜索
穷竭搜索一定会找到最有可能的状态序列,但是算法复杂度是指数级的 \(O(N^L)\)。一种最简化的策略是,每一时刻都只选取下一时刻最可能的状态,显然这种策略没有考虑全局最优,只考虑下一步最优,因此称为贪心策略。当然,贪心策略虽然牺牲全局最优解但是换取了很快的时间复杂度。贪心搜索算法动画如下。
Python 3 实现中我们利用了 numpy 类库,主要是 np.argmax() 可以让代码简洁。代码本质上是两重循环,(一层循环是np.argmax中),对应时间算法复杂度是 \(O(N\times L)\)。
1 | def search_greedy(initial: List, transition: List, L: int) -> Tuple[float, Tuple]: |
Beam 搜索
贪心策略只考虑了下一步的最大概率状态,若我们改进一下贪心策略,将下一步的最大 \(k\) 个状态保留下来就是beam 搜索了。具体来说, \(k\) beam search表示每个阶段保留 \(k\) 个最大概率路径,下一阶段扩展这 \(k\) 条路径至 \(k \times N\) 条路径再选取最大的top k。以上例来说,选取\(k=2\),则初始 \(s_0\)时选取最大概率的两种状态 0和 2,下一阶段 \(s_1\),计算以0和2开始的共 \(2 \times 3\) 条路径,并保留其中最大概率的两条,如此往复。显然,beam search也无法找到全局最优解,但是它能以线性时间复杂度探索更多的路径空间。
以下是Python 3 的代码实现,利用了 PriorityQueue 选取 \(k\) 路径。由于PriorityQueue 无法自定义比较关系,我们定义了 @total_ordering 标注的类来实现比较关心。时间算法复杂度是 \(O(k\times N \times L)\) 。
1 | def search_beam(initial: List, transition: List, L: int, K: int) -> Tuple[float, Tuple]: |
Viterbi 动态规划
和之前TSP 动态规划算法的思想一样,最有可能状态路径问题解法有可以将指数时间复杂度 \(O(N^L)\) 降到多项式时间复杂度 \(O(L \times N \times N)\) 的算法,就是大名鼎鼎的 Viterbi 算法(维特比算法)。核心思想是在每个阶段,用数组保存每个状态结尾路径的阶段最大概率(及其对应路径)。在不考虑优化空间的情况下,我们开一个二维数组 \(dp[][]\),第一维表示阶段序号,第二维表示状态序号。例如,\(dp[1][0]\) 是 \(s_1\) 阶段时以状态0结尾的所有路径中的最大概率,即 \[ dp[1][0] = \max \\{s_0[0] \rightarrow s_1[0], s_0[1] \rightarrow s_1[0], s_0[2] \rightarrow s_1[0]\\} \]
实现代码中没有返回路径本身而只是其概率值,目的是通过简洁的三层循环来表达算法精髓。
1 | def search_dp(initial: List, transition: List, L: int) -> float: |
概率采用
以上所有的算法都是确定性的。在NLP 深度学习decoding 时候会带来一个问题:确定性容易导致生成重复的短语或者句子。比如,确定性算法很容易生成如下句子。
1 | This is the best of best of best of ... |
1 | def search_prob_greedy(initial: List, transition: List, L: int) -> Tuple[float, Tuple]: |
从零构建统计随机变量生成器之离散基础篇
在本系列中,我们会从第一性原理出发,从零开始构建统计学中的常见分布的随机变量生成器,包括二项分布,泊松分布,高斯分布等。在实现这些基础常见分布的过程中,会展示如何使用统计模拟的通用技术,包括 inverse CDF,Box-Muller,分布转换等。本期通过伯努利试验串联起来基础离散分布并通过代码来实现这些分布的生成函数,从零开始构建的原则是随机变量生成器实现只依赖 random() 产生 [0, 1.0] 之间的浮点数,不依赖于其他第三方API来完成。
- 从零构建统计随机变量生成器之 离散基础篇
- 从零构建统计随机变量生成器之 用逆变换采样方法构建随机变量生成器
- 深入 LeetCode 470 拒绝采样,状态转移图求期望和一道经典统计求期望题目
- 从零构建统计随机变量生成器之 正态分布 Box-Muller方法
均匀分布(离散)
离散均匀分布(Discrete Uniform Distribution)的随机变量是最为基本的,图中为 [0, 6] 七个整数的离散均匀分布。算法实现为,使用 [0, 1] 之间的随机数 u,再将 u 等比例扩展到指定的整数上下界。
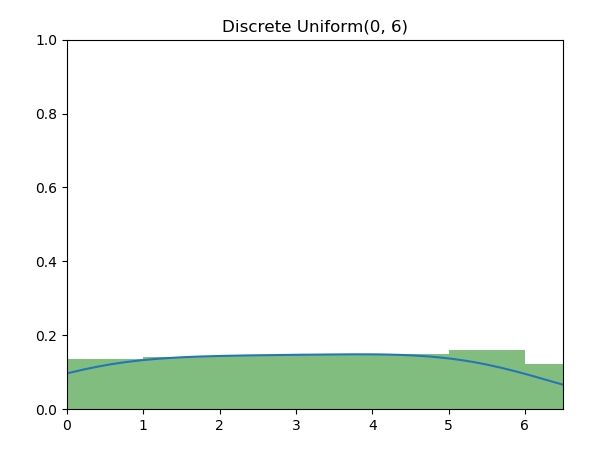
实现代码
1 | import random |
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_uniform.py
伯努利分布
伯努利分布(Bernoulli Distribution)是support为0或者1的离散分布,0和1可以看成失败和成功两种可能。伯努利分布指定了成功的概率p,例如,下图是 p=0.4 的伯努利分布。
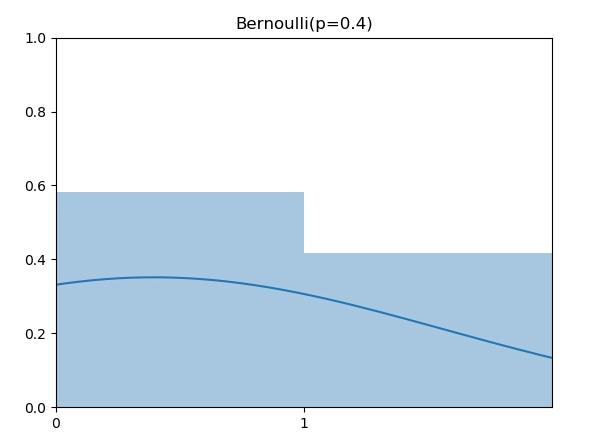
伯努利分布随机数实现也很直接,将随机值 u 根据 p 决定成功或者失败。
实现代码
1 | import random |
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_bernoulli.py
类别分布
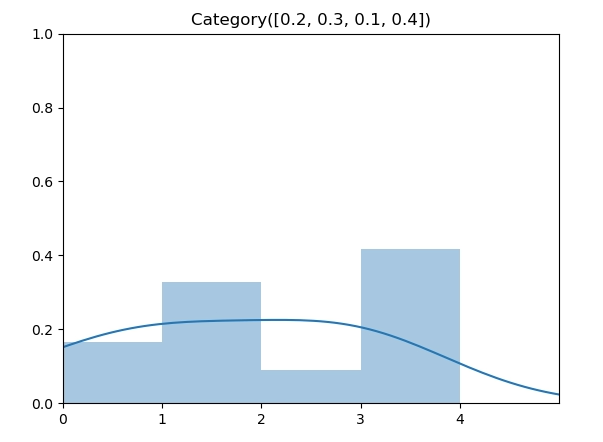
类别分布(Categorical Distribution)是在伯努利分布的基础上扩展到了多个点,每个点同样由参数指定了其概率,因此,其参数从 p 扩展到了向量 \(\vec p\),如图所示为 $p = [0.2, 0.3, 0.1, 0.4] $ 时的类别分布。
实现代码
类别分布生成函数也扩展了伯努利分布的实现算法,将随机数 u 和累计概率向量作比较。在这个例子中, $p = [0.2, 0.3, 0.1, 0.4] $ 转换成 $c = [0.2, 0.5, 0.6, 1] $,再将 u 和 \(\vec c\)数组匹配,返回结果为第一个大于 u 的元素 index。实现上,我们可以以线性复杂度遍历数组,更好一点的方法是,用 python bisect函数通过二分法找到index,将时间复杂度降到 \(O(log(n))\)。
1 | import bisect |
Github 代码地址: https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_categorical.py
二项分布
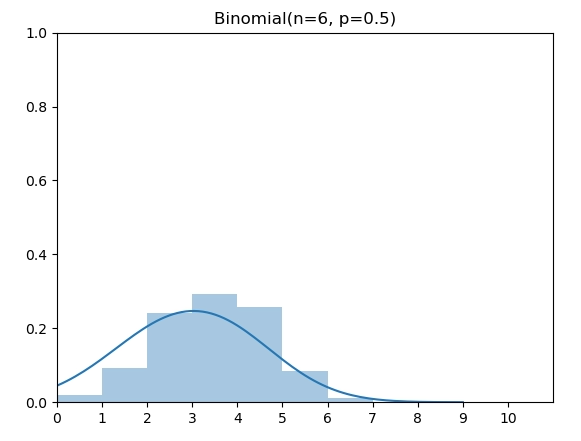
二项分布(Binomial Distribution)有两个参数 n 和 p,表示伯努利实验做n次后成功的次数。图中为 n=6,p=0.5的二项分布。
实现代码
二项分布生成算法可以通过伯努利试验的故事来实现,即调用 n 次伯努利分布生成函数,返回总的成功次数。
1 | def binomial(n: int, p: float) -> int: |
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_binomial.py
概率质量函数(PMF)
\[ \operatorname{Pr}_\text{Binomial}(X=k)=\left(\begin{array}{c}n \\ k\end{array}\right)p^{k}(1- p)^{n-k} \]
几何分布
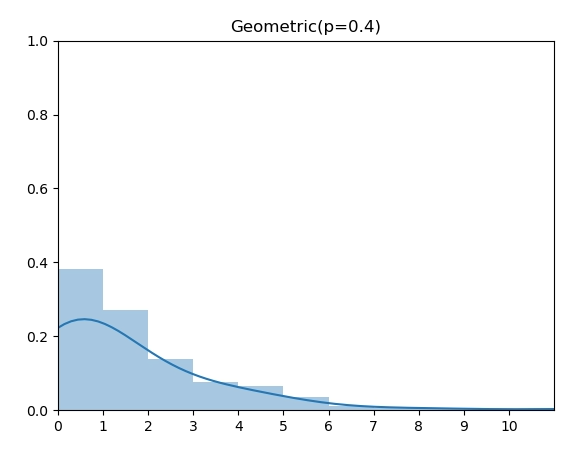
几何分布(Geometric Distribution)和伯努利实验的关系是:几何分布是反复伯努利实验直至第一次成功时的失败次数。如图,当成功概率 p=0.4时的几何分布。
实现代码
1 | from discrete_bernoulli import bernoulli |
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_geometric.py
概率质量函数(PMF)
\[ \operatorname{Pr}_\text{Geometric}(X=k)=(1-p)^{k-1} p \]
负二项分布
负二项分布(Negative Binomial Distribution)是尝试伯努利试验直至成功 r 次的失败次数。
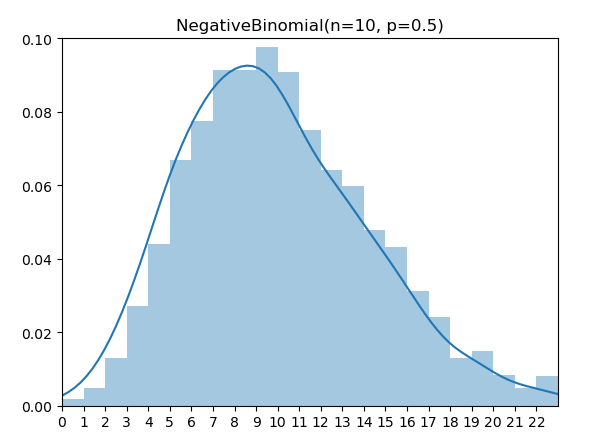
实现代码
1 | from discrete_bernoulli import bernoulli |
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_nagative_binomial.py
概率质量函数(PMF)
\[ \operatorname{Pr}_\text{NegBinomial}(X=k)=\left(\begin{array}{c}k+r-1 \\ r-1\end{array}\right)(1-p)^{k} p^{r} \]
超几何分布
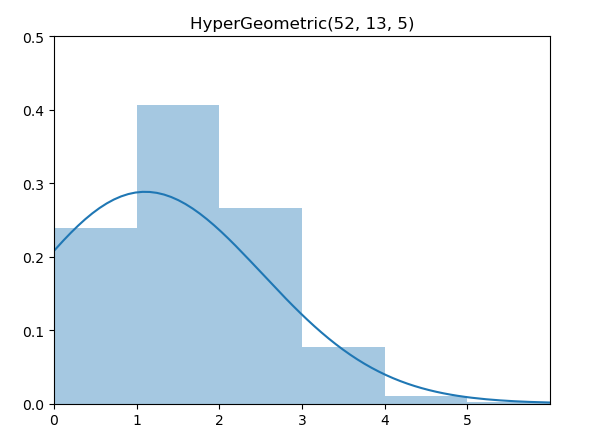
超几何分布(HyperGeometric Distribution)的意义是从总数为N的集合抽取n次后成功的次数。具体来说,集合由K个表示成功的元素和N-K个表示失败的元素组成,并且抽取时没有替换(without replacement)情况下的成功次数。注意,超几何分布和二项分布的区别仅在于有无替换。
实现代码
1 | from discrete_bernoulli import bernoulli |
Github 代码地址:
https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_hypergeometric.py
概率质量函数(PMF)
\[ \operatorname{Pr}_\text{Hypergeo}(X=k)=\frac{\left(\begin{array}{c}K \\ k\end{array}\right)\left(\begin{array}{c}N-k \\ n-k\end{array}\right)}{\left(\begin{array}{l}N \\ n\end{array}\right)} \]
负超几何分布
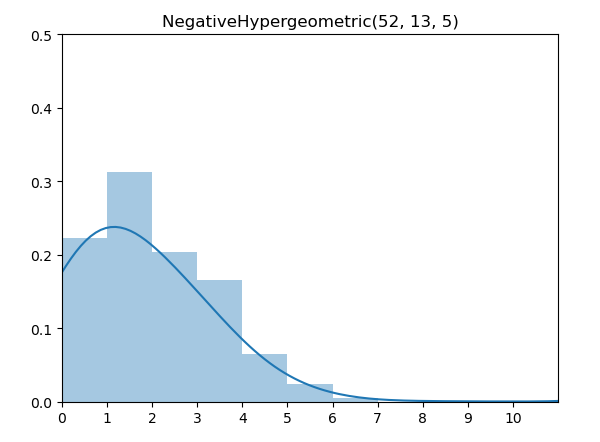
负超几何分布(Negative Hypergeometric Distribution)的意义是从总数为N的集合中,无替换下抽取直至 r 次失败时,成功的次数。
实现代码
1 | from discrete_bernoulli import bernoulli |
Github 代码地址: https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_negative_hypergeometric.py
概率质量函数(PMF)
\[ \operatorname{Pr}_\text{NegHypergeo}(X=k)=\frac{\left(\begin{array}{c}k+r-1 \\ k\end{array}\right)\left(\begin{array}{c}N-r-k \\ K-k\end{array}\right)}{\left(\begin{array}{l}N \\ K\end{array}\right)} \quad \text{for } k=0,1,2, \ldots, K \]
伯努利试验总结
下表总结了上面四种和伯努利试验有关的离散分布的具体区别。
| 有替换 | 无替换 | |
|---|---|---|
| 固定尝试次数 | 二项 Binomial | 超几何 Hypergeometric |
| 固定成功次数 | 负二项 Negative Binomial | 负超几何 Negative Hypergeometric |
分享课程 Berkeley Deep Reinforcement Learning Bootcamp 2017
Berkeley 2017年联合了DeepMind 以及 OpenAI 举办了一个大咖云集的深度强化学习训练营,是难得的前沿深度强化学习佳品,本公众号 MyEncyclopedia 用代码实现了权威教材 Sutton & Barto 第二版强化学习的基础部分之后,会大致沿着这个训练营的思路,从原理到代码逐步揭示强化深度学习面纱,并结合各种有意思的游戏环境来演示。
如果没有耐心的同学可以直接跳到文末的百度云盘下载链接,内容涵盖所有视频和slide。
此次训练营主讲的强化学习领域专家包括
Pieter Abbeel,前Berkeley 机器人学习实验室主任,伯克利人工智能研究(BAIR)实验室联合主任
Andrej Karpathy,前 OpenAI研究科学家、现特斯拉AI总监
Vlad Mnih,Deepmind 研究科学家
John Schulman,Deepmind 研究科学家,OpenAI共同创建人
Sergey Levine,Berkeley 计算机副教授

课程列表
- Core Lecture 1 Intro to MDPs and Exact Solution Methods -- Pieter Abbeel
- Core Lecture 2 Sample-based Approximations and Fitted Learning -- Rocky Duan
- Core Lecture 3 DQN + Variants -- Vlad Mnih
- Core Lecture 4a Policy Gradients and Actor Critic -- Pieter Abbeel
- Core Lecture 4b Pong from Pixels -- Andrej Karpathy
- Core Lecture 5 Natural Policy Gradients, TRPO, and PPO -- John Schulman
- Core Lecture 6 Nuts and Bolts of Deep RL Experimentation -- John Schulman
- Core Lecture 7 SVG, DDPG, and Stochastic Computation Graphs -- John Schulman
- Core Lecture 8 Derivative-free Methods -- Peter Chen
- Core Lecture 9 Model-based RL -- Chelsea Finn
- Core Lecture 10a Utilities -- Pieter Abbeel
- Core Lecture 10b Inverse RL -- Chelsea Finn
- Frontiers Lecture I: Recent Advances, Frontiers and Future of Deep RL -- Vlad Mnih
- Frontiers Lecture II: Recent Advances, Frontiers and Future of Deep RL -- Sergey Levine
- TAs Research Overviews
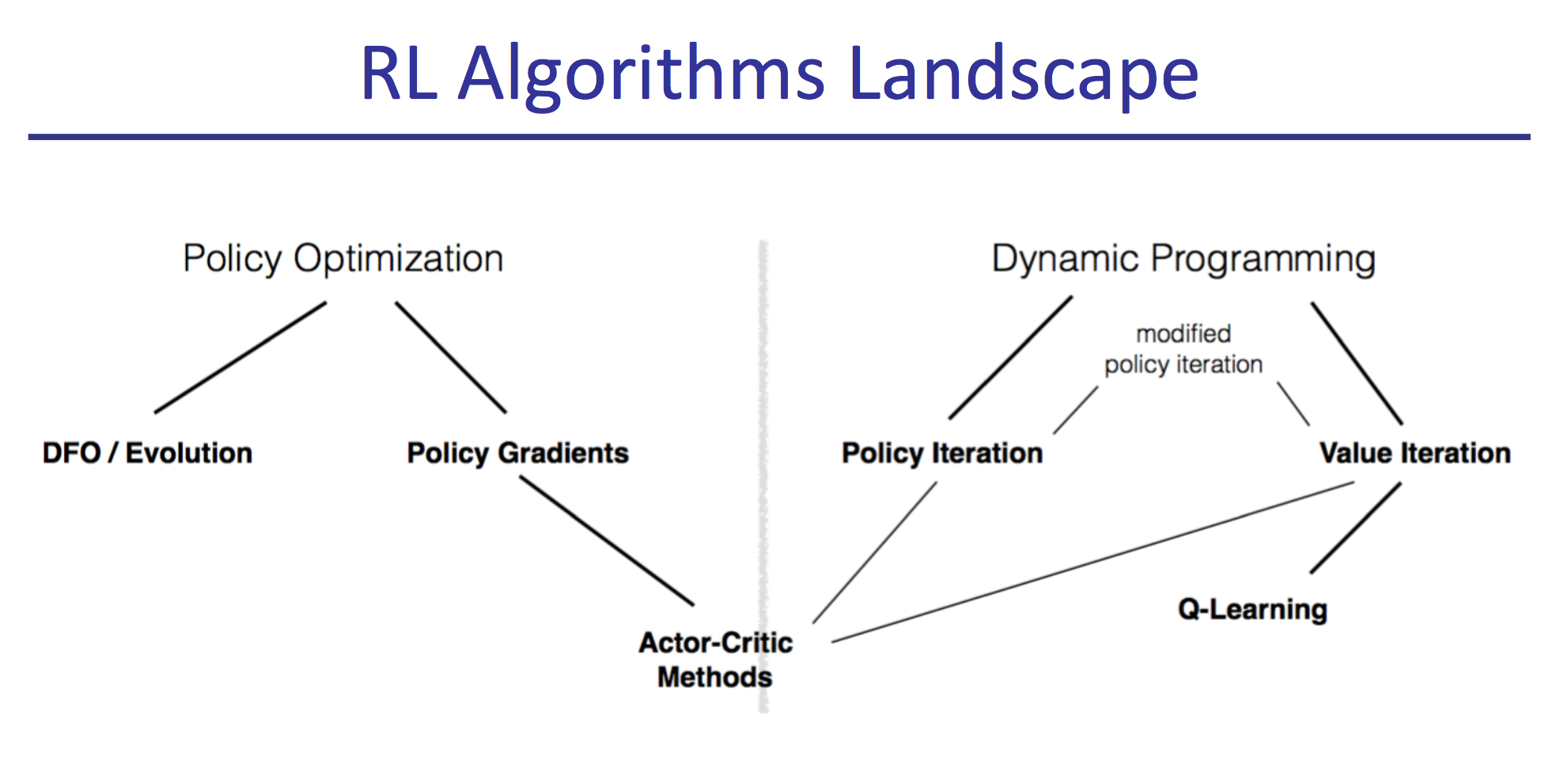
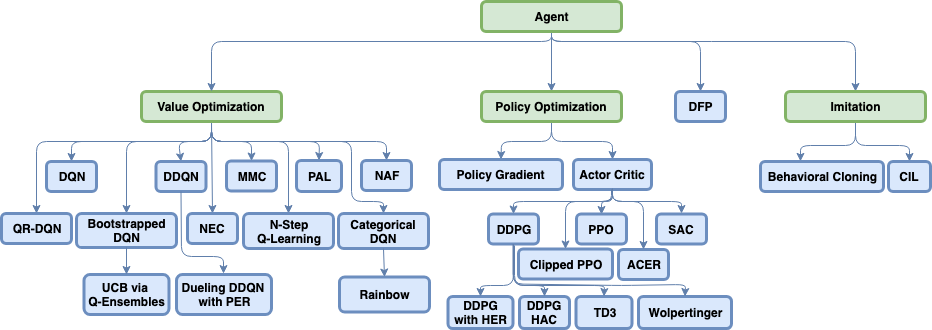
前两讲总结了强化学习基础理论方面,包括用动态规划求精确解,采样与环境交互的传统基本方法。第三四讲覆盖了主流的深度强化学习的几种模式:DQN,PG和AC。第五到七讲深入了深度强化学习的各种前沿方法。值得一提的是第六讲,很好的从实践中总结了各种调试诊断方法。余下的若干讲涉及到了非主流的剩余强化学习领域。
下载方法
关注 MyEncyclopedia 公众号,输入 rl-bootcamp-ucb-2017 即可获得百度云盘链接