TSP From DP to Deep Learning. Episode 3: Pointer Network

This is third episode of series: TSP From DP to Deep Learning. In this episode, we will be entering the realm of deep learning, specifically, a type of sequence-to-sequence called Pointer Networks is introduced. It is tailored to solve problems like TSP or Convex Hull. Full list of this series is listed below.

• Episode 1: AC TSP on AIZU with recursive DP

• Episode 2: TSP DP on a Euclidean Dataset

• Episode 3: Pointer Networks in PyTorch

• Episode 4: Search for Most Likely Sequence

• Episode 5: Reinforcement Learning PyTorch Implementation

Pointer Networks

In traditional sequence-to-sequence RNN, output classes depend on pre-defined size. For instance, a word generating RNN will utter one word from vocabulary of \(|V|\) size at each time step. However, there is large set of problems such as Convex Hull, Delaunay Triangulation and TSP, where range of the each output is not pre-defined, but of variable size, defined by the input. Pointer Networks overcame the constraint by selecting \(i\) -th input with probability derived from attention score.

Convex Hull

In following example, 10 points are given, the output is a sequence of points that bounds the set of all points. Each value in the output sequence is a integer ranging from 1 to 10, in this case, which is the value given by the concrete example. Generally, finding exact solution has been proven to be equivelent to sort problem, and has time complexity \(O(n*log(n))\).

image info

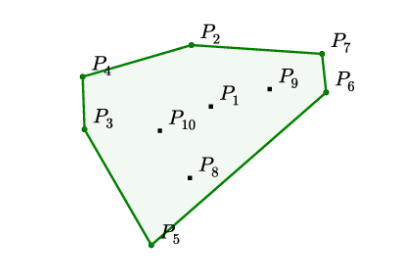
\[ \begin{align*} &\text{Input: } \mathcal{P} &=& \left\{P_{1}, \ldots, P_{10} \right\} \\ &\text{Output: } C^{\mathcal{P}} &=& \{2,4,3,5,6,7,2\} \end{align*} \]

TSP

TSP is almost identical to Convex Hull problem, though output sequence is of fixed length. In previous epsiode, we reduced from \(O(n!)\) to \(O(n^2*2^n)\).

image info

\[ \begin{align*} &\text{Input: } \mathcal{P} &= &\left\{P_{1}, \ldots, P_{6} \right\} \\ &\text{Output: } C^{\mathcal{P}} &=& \{1,3,2,4,5,6,1\} \end{align*} \]

Delaunay Triangulation

A Delaunay triangulation for a set of points in a plane is a triangulation such that each circumcircle of every triangle is empty, meaning no point from \(\mathcal{P}\) in its interior. This kind of problem outputs a sequence of sets, and each item in the set ranges from the input set \(\mathcal{P}\).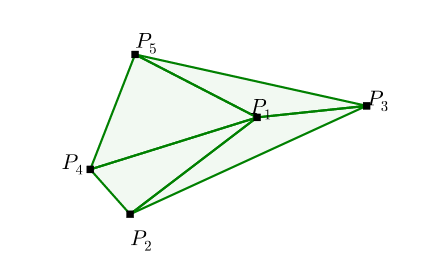

\[ \begin{align*} &\text{Input: } \mathcal{P} &=& \left\{P_{1}, \ldots, P_{5} \right\} \\ &\text{Output: } C^{\mathcal{P}} &=& \{(1,2,4),(1,4,5),(1,3,5),(1,2,3)\} \end{align*} \]

Sequence-to-Sequence Model

Suppose now n is fixed. given a training pair, \((\mathcal{P}, C^{\mathcal{P}})\), the vanilla sequence-to-sequence model parameterized by \(\theta\) computes the conditional probability.

\[ \begin{equation} p\left(\mathcal{C}^{\mathcal{P}} | \mathcal{P} ; \theta\right)=\prod_{i=1}^{m(\mathcal{P})} p\left(C_{i} | C_{1}, \ldots, C_{i-1}, \mathcal{P} ; \theta\right) \end{equation} \] The parameters of the model are learnt by maximizing the conditional probabilities for the training set, i.e. \[ \begin{equation} \theta^{*}=\underset{\theta}{\arg \max } \sum_{\mathcal{P}, \mathcal{C}^{\mathcal{P}}} \log p\left(\mathcal{C}^{\mathcal{P}} | \mathcal{P} ; \theta\right) \end{equation} \]

Content Based Input Attention

When attention is applied to vanilla sequence-to-sequence model, better result is obtained.

Let encoder and decoder states be $ (e_{1}, , e_{n}) $ and $ (d_{1}, , d_{m()}) $, respectively. At each output time \(i\), compute the attention vector \(d_i\) to be linear combination of $ (e_{1}, , e_{n}) $ with weights $ (a_{1}^{i}, , a_{n}^{i}) $ \[ d_{i} = \sum_{j=1}^{n} a_{j}^{i} e_{j} \]

$ (a_{1}^{i}, , a_{n}^{i}) $ is softmax value of $ (u_{1}^{i}, , u_{n}^{i}) $ and \(u_{j}^{i}\) can be considered as distance between \(d_{i}\) and \(e_{j}\). Notice that \(v\), \(W_1\), and \(W_2\) are learnable parameters of the model.

\[ \begin{eqnarray} u_{j}^{i} &=& v^{T} \tanh \left(W_{1} e_{j}+W_{2} d_\right) \quad j \in(1, \ldots, n) \\ a_{j}^{i} &=& \operatorname{softmax}\left(u_{j}^{i}\right) \quad j \in(1, \ldots, n) \end{eqnarray} \]

Pointer Networks

image info

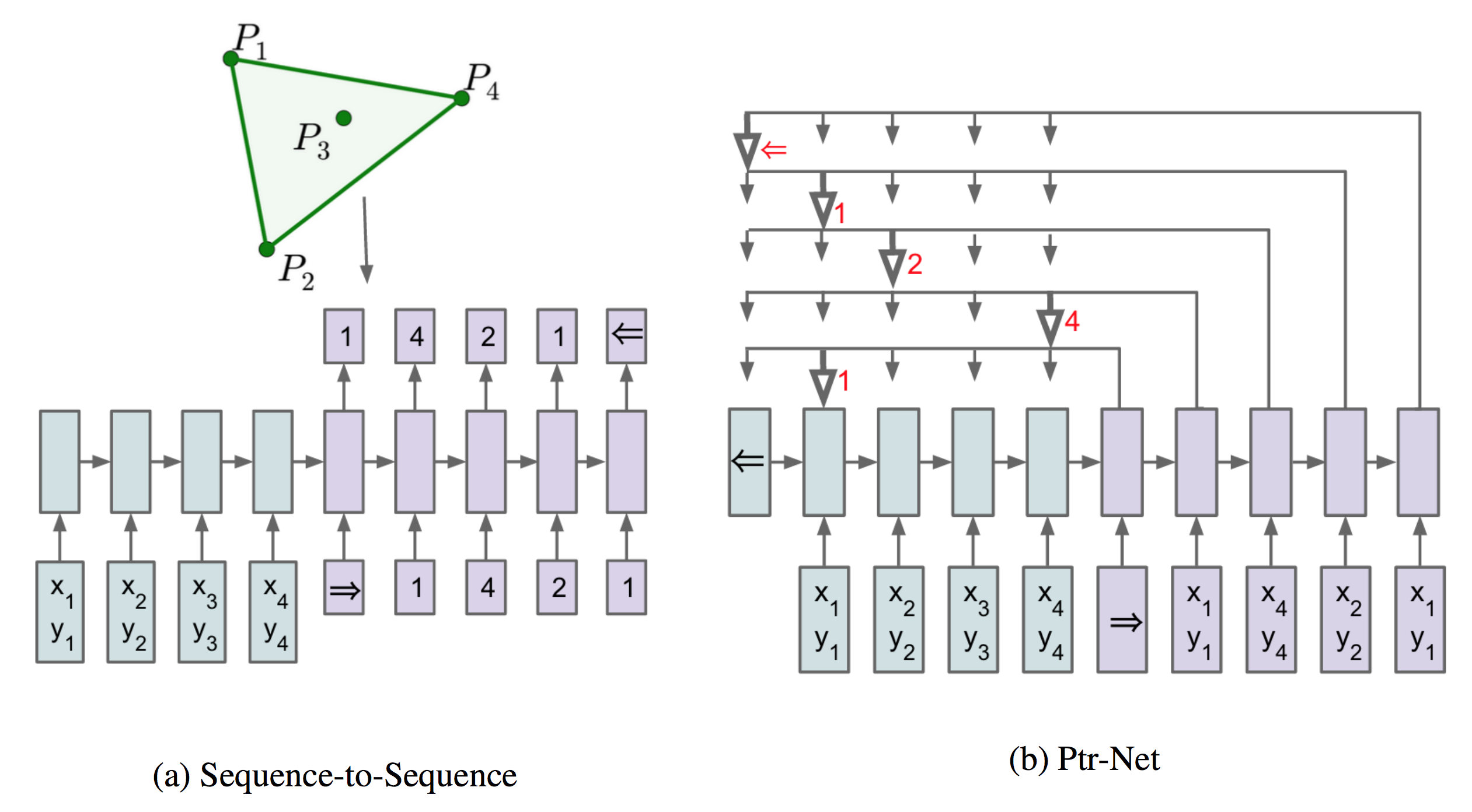
Pointer Networks does not blend the encoder state \(e_j\) to propagate extra information to the decoder, but instead, use \(u^i_j\) as pointers to the input element.

\[ \begin{eqnarray*} u_{j}^{i} &=& v^{T} \tanh \left(W_{1} e_{j}+W_{2} d_{i}\right) \quad j \in(1, \ldots, n) \\ p\left(C_{i} | C_{1}, \ldots, C_{i-1}, \mathcal{P}\right) &=& \operatorname{softmax}\left(u^{i}\right) \end{eqnarray*} \]

More on Attention

In FloydHub Blog - Attention Mechanism , a clear and detailed explanation of difference and similarity between the classic first type of Attention, commonly referred to as Additive Attention by Dzmitry Bahdanau and second classic type, known as Multiplicative Attention and proposed by Thang Luong , is discussed.

It's well known that in Luong Attention, three ways of alignment scoring function is defined, or the distance between \(d_{i}\) and \(e_{j}\).

\[ \operatorname{score} \left( d_i, e_j \right)= \begin{cases} d_i^{\top} e_j & \text { dot } \\ d_i^{\top} W_a e_j & \text { general } \\ v_a^{\top} \tanh \left( W_a \left[ d_i ; e_j \right] \right) & \text { concat } \end{cases} \]

PyTorch Implementation

In episode 2, we have introduced TSP dataset where each case is a line, of following form.

x0, y0, x1, y1, ... output 1 v1 v2 v3 ... 1

PyTorch Dataset

Each case is converted to (input, input_len, output_in, output_out, output_len) of type nd.ndarray with appropriate padding and encapsulated in a extended PyTorch Dataset.

{linenos

from torch.utils.data import Dataset

class TSPDataset(Dataset):
	"each data item of form (input, input_len, output_in, output_out, output_len)"
	data: List[Tuple[np.ndarray, np.ndarray, np.ndarray, np.ndarray, np.ndarray]]
	
	def __len__(self):
		return len(self.data)

	def __getitem__(self, index):
		input, input_len, output_in, output_out, output_len = self.data[index]
		return input, input_len, output_in, output_out, output_len

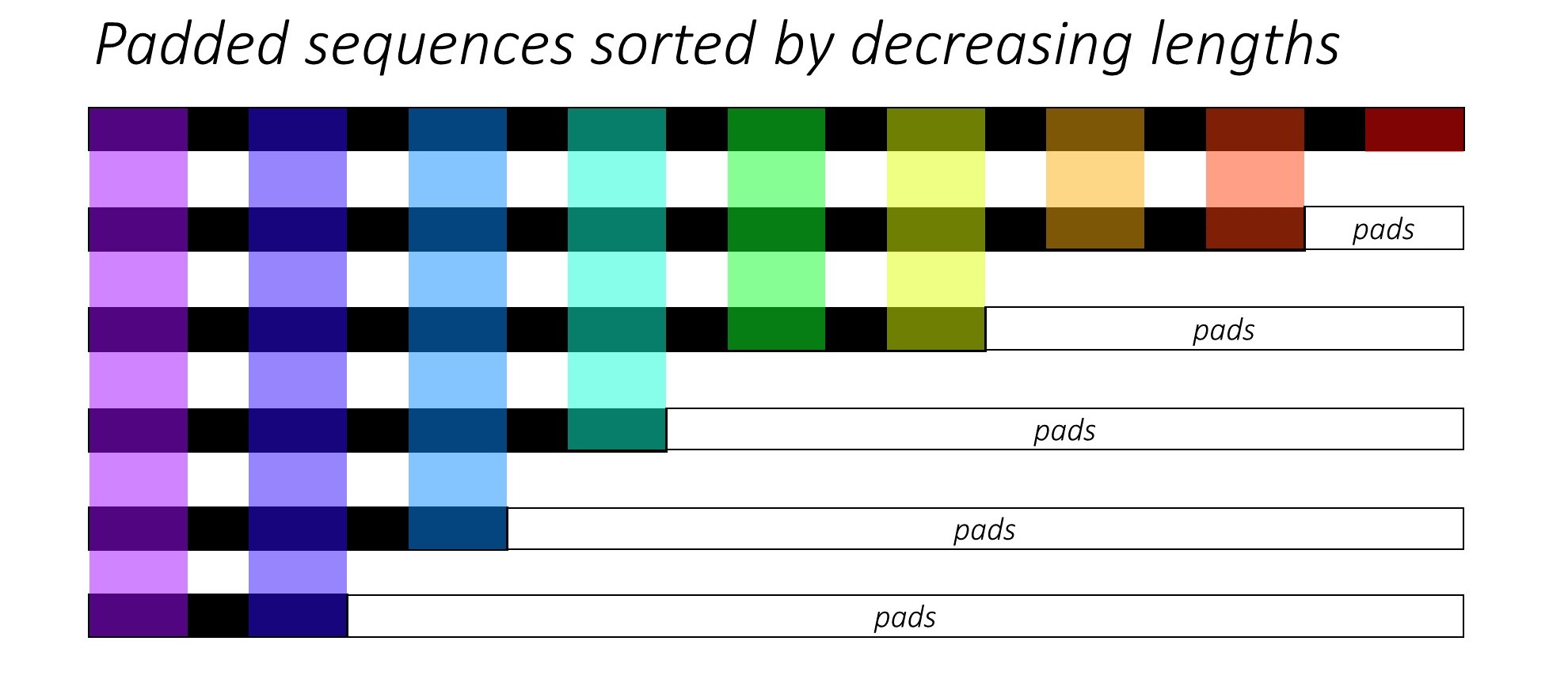
PyTorch pad_packed_sequence

Code in PyTorch seq-to-seq model typically utilizes pack_padded_sequence and pad_packed_sequence API to reduce computational cost. A detailed explanation is given here https://github.com/sgrvinod/a-PyTorch-Tutorial-to-Image-Captioning#decoder-1.

image info

{linenos

class RNNEncoder(nn.Module):
	rnn: Union[nn.LSTM, nn.GRU, nn.RNN]

	def __init__(self, rnn_type: str, bidirectional: bool, num_layers: int, input_size: int, hidden_size: int, dropout: float):
		super(RNNEncoder, self).__init__()
		if bidirectional:
			assert hidden_size % 2 == 0
			hidden_size = hidden_size // 2
		self.rnn = rnn_init(rnn_type, input_size=input_size, hidden_size=hidden_size, bidirectional=bidirectional,num_layers=num_layers, dropout=dropout)

	def forward(self, src: Tensor, src_lengths: Tensor, hidden: Tensor = None) -> Tuple[Tensor, Tensor]:
		lengths = src_lengths.view(-1).tolist()
		packed_src = pack_padded_sequence(src, lengths)
		memory_bank, hidden_final = self.rnn(packed_src, hidden)
		memory_bank = pad_packed_sequence(memory_bank)[0]
		return memory_bank, hidden_final

Attention Code

{linenos

class Attention(nn.Module):
	linear_out: nn.Linear

	def __init__(self, dim: int):
		super(Attention, self).__init__()
		self.linear_out = nn.Linear(dim * 2, dim, bias=False)

	def score(self, src: Tensor, target: Tensor) -> Tensor:
		batch_size, src_len, dim = src.size()
		_, target_len, _ = target.size()
		target_ = target
		src_ = src.transpose(1, 2)
		return torch.bmm(target_, src_)

	def forward(self, src: Tensor, target: Tensor, src_lengths: Tensor) -> Tuple[Tensor, Tensor]:
		assert target.dim() == 3

		batch_size, src_len, dim = src.size()
		_, target_len, _ = target.size()

		align_score = self.score(src, target)

		mask = sequence_mask(src_lengths)
		# (batch_size, max_len) -> (batch_size, 1, max_len)
		mask = mask.unsqueeze(1)
		align_score.data.masked_fill_(~mask, -float('inf'))
		align_score = F.softmax(align_score, -1)

		c = torch.bmm(align_score, src)

		concat_c = torch.cat([c, target], -1)
		attn_h = self.linear_out(concat_c)

		return attn_h, align_score

Complete PyTorch implementation source code is also available on github.

References