TSP From DP to Deep Learning. Episode 5: Reinforcement Learning
This is fifth episode of series: TSP From DP to Deep Learning. In this episode, we turn to Reinforcement Learning technology, in particular, a model-free policy gradient method that embeds pointer network to learn minimal tour without supervised best tour label in dataset. Full list of this series is listed below.
Episode 1: AC TSP on AIZU with recursive DP
Episode 2: TSP DP on a Euclidean Dataset
Episode 3: Pointer Networks in PyTorch
Episode 4: Search for Most Likely Sequence
Pointer Network Refresher
In previous episode Pointer Networks in PyTorch, we implemented Pointer Networks in PyTorch with a 2D Euclidean dataset.
Recall that the input is a graph as a sequence of \(n\) cities in a two dimensional space\[ s=\{\mathbf{x_i}\}_{i=1}^n, \mathbf{x}_{i} \in \mathbb{R}^{2} \]
The output is a permutation of the points \(\pi\), that visits each city exactly once and returns to starting point with minimal distance.
Let us define the total distance of a \(\pi\) with respect to \(s\) as \(L\)
\[ L(\pi | s)=\left\|\mathbf{x}_{\pi(n)}-\mathbf{x}_{\pi(1)}\right\|_{2}+\sum_{i=1}^{n-1}\left\|\mathbf{x}_{\pi(i)}-\mathbf{x}_{\pi(i+1)}\right\|_{2} \]
The stochastic policy \(p(\pi | s; \theta)\), parameterized by \(\theta\), is aiming to assign high probabilities to short tours and low probabilities to long tours. The joint probability assumes independency to allow factorization.
\[ p(\pi | s; \theta) = \prod_{i=1}^{n} p\left({\pi(i)} | {\pi(1)}, \ldots, {\pi(i-1)} , s; \theta\right) \]
The loss of the model is cross entropy between the network’s output probabilities \(\pi\) and the best tour \(\hat{\pi}\) generated by a TSP solver.
Contribution made by Pointer networks is that it addressed the constraint in that it allows for dynamic index value given by the particular test case, instead of from a fixed-size vocabulary.
Reinforcement Learning
Neural Combinatorial Optimization with Reinforcement Learning combines the power of Reinforcement Learning (RL) and Deep Learning to further eliminate the constraint required by Pointer Networks that the training dataset has to have supervised labels of best tour. With deep RL, test cases do not need to have a solution which is common pattern in deep RL. In the paper, a model-free policy-based RL method is adopted.
Model-Free Policy Gradient Methods
In the authoritative RL book, chapter 8 Planning and Learning with Tabular Methods, there are two major approaches in RL. One is model-based RL and the other is model-free RL. Distinction between the two relies on concept of model, which is stated as follows:
By a model of the environment we mean anything that an agent can use to predict how the environment will respond to its actions.
So model-based methods demand a model of the environment, and hence dynamic programming and heuristic search fall into this category. With model in mind, utility of the state can be computed in various ways and planning stage that essentially builds policy is needed before agent can take any action. In contrast, model-free methods, without building a model, are more direct, ignoring irrelevant information and just focusing on the policy which is ultimately needed. Typical examples of model-free methods are Monte Carlo Control and Temporal-Difference Learning. >Model-based methods rely on planning as their primary component, while model-free methods primarily rely on learning.
In TSP problem, the model is fully determined by all points given, and no feedback is generated for each decision made. So it's unclear to how to map state value with a tour. Therefore, we turn to model-free methods. In chapter 13 Policy Gradient Methods, a particular approximation model-free method that learns a parameterized policy that can select actions without consulting a value function. This approach fits perfectly with aforementioned pointer networks where the parameterized policy \(p(\pi | s; \theta)\) is already defined.
Training objective is obvious, the expected tour length of \(\pi_\theta\) which, given an input graph \(s\)\[ J(\theta | s) = \mathbb{E}_{\pi \sim p_{\theta}(\cdot | s)} L(\pi | s) \]
Monte Carlo Policy Gradient: REINFORCE with Baseline
In order to find largest reward, a typical way is to optimize the parameters \(\theta\) in the direction of derivative: \(\nabla_{\theta} J(\theta | s)\).
\[ \nabla_{\theta} J(\theta | s)=\nabla_{\theta} \mathbb{E}_{\pi \sim p_{\theta}(\cdot | s)} L(\pi | s) \]
RHS of equation above is the derivative of expectation that we have no idea how to compute or approximate. Here comes the well-known REINFORCE trick that turns it into form of expectation of derivative, which can be approximated easily with Monte Carlo sampling, where the expectation is replaced by averaging.
\[ \nabla_{\theta} J(\theta | s)=\mathbb{E}_{\pi \sim p_{\theta}(. | s)}\left[L(\pi | s) \nabla_{\theta} \log p_{\theta}(\pi | s)\right] \]
Another common trick, subtracting a baseline \(b(s)\), leads the derivative of reward to the following equation. Note that \(b(s)\) denotes a baseline function that must not depend on \(\pi\). \[ \nabla_{\theta} J(\theta | s)=\mathbb{E}_{\pi \sim p_{\theta}(. | s)}\left[(L(\pi | s)-b(s)) \nabla_{\theta} \log p_{\theta}(\pi | s)\right] \]
The trick is explained in as:
Because the baseline could be uniformly zero, this update is a strict generalization of REINFORCE. In general, the baseline leaves the expected value of the update unchanged, but it can have a large effect on its variance.
Finally, the equation can be approximated with Monte Carlo sampling, assuming drawing \(B\) i.i.d: \(s_{1}, s_{2}, \ldots, s_{B} \sim \mathcal{S}\) and sampling a single tour per graph: $ {i} p{}(. | s_{i}) $, as follows \[ \nabla_{\theta} J(\theta) \approx \frac{1}{B} \sum_{i=1}^{B}\left(L\left(\pi_{i} | s_{i}\right)-b\left(s_{i}\right)\right) \nabla_{\theta} \log p_{\theta}\left(\pi_{i} | s_{i}\right) \]
Actor Critic Methods
REINFORCE with baseline works quite well but it also has disadvantage.
REINFORCE with baseline is unbiased and will converge asymptotically to a local minimum, but like all Monte Carlo methods it tends to learn slowly (produce estimates of high variance) and to be inconvenient to implement online or for continuing problems.
A typical improvement is actor–critic methods, that not only learn approximate policy, the actor job, but also learn approximate value funciton, the critic job. This is because it reduces variance and accelerates learning via a bootstrapping critic that introduce bias which is often beneficial. Detailed algorithm in the paper illustrated below.
\[ \begin{align*} &\textbf{Algorithm Actor-critic training} \\ &1: \quad \textbf{ procedure } \text{ TRAIN(training set }S \text{, training steps }T \text{, batch size } B \text{)} \\ &2: \quad \quad \text{Initialize pointer network params } \theta \\ &3: \quad \quad \text{Initialize critic network params } \theta_{v} \\ &4: \quad \quad \textbf{for }t=1 \text{ to } T \textbf{ do }\\ &5: \quad \quad \quad s_{i} \sim \operatorname{SAMPLE INPUT } (S) \text{ for } i \in\{1, \ldots, B\} \\ &6: \quad \quad \quad \pi_{i} \sim \operatorname{SAMPLE SOLUTION } \left(p_{\theta}\left(\cdot | s_{i}\right)\right) \text{ for } i \in\{1, \ldots, B\} \\ &7: \quad \quad \quad b_{i} \leftarrow b_{\theta_{v}}\left(s_{i}\right) \text{ for } i \in\{1, \ldots, B\} \\ &8: \quad \quad \quad g_{\theta} \leftarrow \frac{1}{B} \sum_{i=1}^{B}\left(L\left(\pi_{i} | s_{i}\right)-b_{i}\right) \nabla_{\theta} \log p_{\theta}\left(\pi_{i} | s_{i}\right) \\ &9: \quad \quad \quad \mathcal{L}_{v} \leftarrow \frac{1}{B} \sum_{i=1}^{B} \left\| b_{i}-L\left(\pi_{i}\right) \right\| _{2}^{2} \\ &10: \quad \quad \quad \theta \leftarrow \operatorname{ADAM} \left( \theta, g_{\theta} \right) \\ &11: \quad \quad \quad \theta_{v} \leftarrow \operatorname{ADAM}\left(\theta_{v}, \nabla_{\theta_{v}} \mathcal{L}_{v}\right) \\ &12: \quad \quad \textbf{end for} \\ &13: \quad \textbf{return } \theta \\ &14: \textbf{end procedure} \end{align*} \]
Implementation in PyTorch
Beam Search in OpenNMT-py
In Episode 4 Search for Most Likely Sequence, an 3x3 rectangle trellis is given and several decoding methods are illustrated in plain python. In PyTorch version, there is a package OpenNMT-py that supports efficient batched beam search. But due to its complicated BeamSearch usage, previous problem is demonstrated using its API. For its details, please refer to Implementing Beam Search — Part 1: A Source Code Analysis of OpenNMT-py
1 | from copy import deepcopy |
The output is as follows. When \(k=2\) and 3 steps, the most likely sequence is \(0 \rightarrow 1 \rightarrow 0\), whose probability is 0.084.
1 | step 0 beam results: |
RL with PointerNetwork
The complete code is on github TSP RL. Below are partial core classes.
1 | class CombinatorialRL(nn.Module): |
References
TSP From DP to Deep Learning. Episode 4: Search for Most Likely Sequence
This is fourth episode of series: TSP From DP to Deep Learning. In this episode, we systematically compare different searching algorithms for finding most likely sequence in the context of simplied markov chain setting. These models can be further utilized in deep learning decoding stage, which will be illustrated in reinforcement learning, in the next episode. Full list of this series is listed below.
Episode 1: AC TSP on AIZU with recursive DP
Episode 2: TSP DP on a Euclidean Dataset
Episode 3: Pointer Networks in PyTorch
Episode 4: Search for Most Likely Sequence
Problem as Markov Chain
In sequence-to-sequence problem, we are always faced with same problem of determining the best or most likely sequence of output. This kind of recurring problem exists extensively in algorithms, machine learning where we are given initial states and the dynamics of the system, and the goal is to find a path that is most likely. The corresponding concept, in science or mathematical discipline, is called Markov Chain.
Let describe the problem in the context of markov chain. Suppose there are \(n\) states, and initial state is given by $s_0 = [0.35, 0.25, 0.4] $. The transition matrix is defined by \(T\) where $ T[i][j]$ denotes the probability of transitioning from \(i\) to \(j\). Notice that each row sums to \(1.0\). \[ T= \begin{matrix} & \begin{matrix}0&1&2\end{matrix} \\\\ \begin{matrix}0\\\\1\\\\2\end{matrix} & \begin{bmatrix}0.3&0.6&0.1\\\\0.4&0.2&0.4\\\\0.3&0.3&0.4\end{bmatrix}\\\\ \end{matrix} \]
Probability of the next state \(s_1\) is derived by multiplication of \(s_0\) and \(T\), which can be visually interpreted by animation below.
The actual probability distribution value of \(s_1\) is computed numerically below. Recall that left multiplying a row with a matrix amounts to making a linear combination of that row vector.
\[ s_1 = \begin{bmatrix}0.35& 0.25& 0.4\end{bmatrix} \begin{matrix} \begin{bmatrix}0.3&0.6&0.1\\\\0.4&0.2&0.4\\\\0.3&0.3&0.4\end{bmatrix}\\\\ \end{matrix} = \begin{bmatrix}0.325& 0.35& 0.255\end{bmatrix} \] Again, state \(s_2\) can be derived in the same way \(s_1 \times T\), where we assume the transitioning dynamics remains the same. However, in deep learning problem, the dynamics usually depends on \(s_i\), or vary according to the stage.
Suppose there are only 3 stages in our problem, e.g., \(s_0 \rightarrow s_1 \rightarrow s_2\). Let \(L\) be the number of stages and \(N\) be the number of vertices in each stage. Hence \(L=N=3\) in our problem setting. There could be \(N^L\) different paths starting from initial stage and to final stage.
Let us compute an arbitrary path probability as an example, \(2(s_0) \rightarrow 1(s_1) \rightarrow 2(s_2)\). The total probability is
\[ p(2 \rightarrow 1 \rightarrow 2) = s_0[2] \times T[2][1] \times T[1][2] = 0.4 \times 0.3 \times 0.4 = 0.048 \]
Exhaustive Search
First, we implement \(N^L\) exhaustive or brute force search.
The following Python 3 function returns one most likely sequence and its probability. Running the algorithm with our example produces 0.084 and route \(0 \rightarrow 1 \rightarrow 2\).
1 | def search_brute_force(initial: List, transition: List, L: int) -> Tuple[float, Tuple]: |
Greedy Search
Exhaustive search always generates most likely sequence, as searching for a needle in the hay at the cost of exponential runtime complexity \(O(N^L)\). The simplest strategy, unknown as greedy, identifies one vertex in each stage and then expand the vertex in next stage. This strategy, of course, is not guaranteed to find most likely sequence but is fast. See animation below.
Code in Python 3 is given below. Numpy package is employed to utilize np.argmax() for code clarity. Notice there are 2 for loops (the other is np.argmax) so the runtime complexity is \(O(N\times L)\).
1 | def search_greedy(initial: List, transition: List, L: int) -> Tuple[float, Tuple]: |
Beam Search
We could improve greedy strategy a little bit by expanding more vertices in each stage. In beam search with \(k\) nodes, the strategy is in each stage, identify \(k\) nodes with highest probability and expand these \(k\) nodes into next stage. In our example, \(k=2\), we select first 2 nodes in stage \(s_0\), expand these 2 nodes and evaluate \(2 \times 3\) nodes in stage \(s_1\), then select 2 nodes and evaluate 6 nodes in stage \(s_2\). Beam search, similar to greedy strategy, is not guaranteed to find most likely sequence but it extends search space with linear complexity.
Below is implementation in Python 3 with PriorityQueue to select top \(k\) nodes. Notice in order to use reverse order of PriorityQueue, a class with @total_ordering is required to be defined. The runtime complexity is \(O(k\times N \times L)\) .
1 | def search_beam(initial: List, transition: List, L: int, K: int) -> Tuple[float, Tuple]: |
Viterbi DP
Similarly to TSP DP version, there is a dynamic programming approach, widely known as Viterbi algorithm, that always finds out sequence with max probability while reducing runtime complexity from \(O(N^L)\) to \(O(L \times N \times N)\) (corresponding to 3 loops in code below). The core idea is in each stage, an array keeps most likely sequence ending with each vertex and use the dp array as input to next stage. For example, let \(dp[1][0]\) be the most likely probability in \(s_1\) stage and end with vertex 0. \[ dp[1][0] = \max \\{s_0[0] \rightarrow s_1[0], s_0[1] \rightarrow s_1[0], s_0[2] \rightarrow s_1[0]\\} \]
Illustrative code that returns max probability but not route, in order to emphasize 3 loop pattern and max operation, honoring the essence of the algorithm.
1 | def search_dp(initial: List, transition: List, L: int) -> float: |
Probabilistic Sampling
All algorithms described above are deterministic. However, in NLP deep learning decoding, deterministic property has disadvantage in that it may get trapped into repeated phrases or sentences. For example, paragraph like below is commonly generated:
1 | This is the best of best of best of ... |
For demonstration purpose, here is the code based on greedy strategy which probabilistically determines one node at each stage.
1 | def search_prob_greedy(initial: List, transition: List, L: int) -> Tuple[float, Tuple]: |
TSP From DP to Deep Learning. Episode 3: Pointer Network
This is third episode of series: TSP From DP to Deep Learning. In this episode, we will be entering the realm of deep learning, specifically, a type of sequence-to-sequence called Pointer Networks is introduced. It is tailored to solve problems like TSP or Convex Hull. Full list of this series is listed below.
Episode 1: AC TSP on AIZU with recursive DP
Episode 2: TSP DP on a Euclidean Dataset
Episode 3: Pointer Networks in PyTorch
Episode 4: Search for Most Likely Sequence
Pointer Networks
In traditional sequence-to-sequence RNN, output classes depend on pre-defined size. For instance, a word generating RNN will utter one word from vocabulary of \(|V|\) size at each time step. However, there is large set of problems such as Convex Hull, Delaunay Triangulation and TSP, where range of the each output is not pre-defined, but of variable size, defined by the input. Pointer Networks overcame the constraint by selecting \(i\) -th input with probability derived from attention score.
Convex Hull
In following example, 10 points are given, the output is a sequence of points that bounds the set of all points. Each value in the output sequence is a integer ranging from 1 to 10, in this case, which is the value given by the concrete example. Generally, finding exact solution has been proven to be equivelent to sort problem, and has time complexity \(O(n*log(n))\).
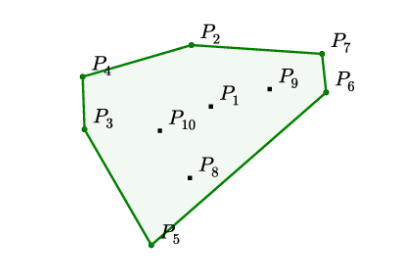
\[ \begin{align*} &\text{Input: } \mathcal{P} &=& \left\{P_{1}, \ldots, P_{10} \right\} \\ &\text{Output: } C^{\mathcal{P}} &=& \{2,4,3,5,6,7,2\} \end{align*} \]
TSP
TSP is almost identical to Convex Hull problem, though output sequence is of fixed length. In previous epsiode, we reduced from \(O(n!)\) to \(O(n^2*2^n)\).
\[ \begin{align*} &\text{Input: } \mathcal{P} &= &\left\{P_{1}, \ldots, P_{6} \right\} \\ &\text{Output: } C^{\mathcal{P}} &=& \{1,3,2,4,5,6,1\} \end{align*} \]
Delaunay Triangulation
A Delaunay triangulation for a set of points in a plane is a
triangulation such that each circumcircle of every triangle is empty,
meaning no point from \(\mathcal{P}\)
in its interior. This kind of problem outputs a sequence of sets, and
each item in the set ranges from the input set \(\mathcal{P}\). 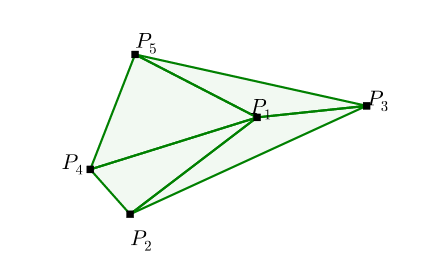
\[ \begin{align*} &\text{Input: } \mathcal{P} &=& \left\{P_{1}, \ldots, P_{5} \right\} \\ &\text{Output: } C^{\mathcal{P}} &=& \{(1,2,4),(1,4,5),(1,3,5),(1,2,3)\} \end{align*} \]
Sequence-to-Sequence Model
Suppose now n is fixed. given a training pair, \((\mathcal{P}, C^{\mathcal{P}})\), the vanilla sequence-to-sequence model parameterized by \(\theta\) computes the conditional probability.
\[ \begin{equation} p\left(\mathcal{C}^{\mathcal{P}} | \mathcal{P} ; \theta\right)=\prod_{i=1}^{m(\mathcal{P})} p\left(C_{i} | C_{1}, \ldots, C_{i-1}, \mathcal{P} ; \theta\right) \end{equation} \] The parameters of the model are learnt by maximizing the conditional probabilities for the training set, i.e. \[ \begin{equation} \theta^{*}=\underset{\theta}{\arg \max } \sum_{\mathcal{P}, \mathcal{C}^{\mathcal{P}}} \log p\left(\mathcal{C}^{\mathcal{P}} | \mathcal{P} ; \theta\right) \end{equation} \]
Content Based Input Attention
When attention is applied to vanilla sequence-to-sequence model, better result is obtained.
Let encoder and decoder states be $ (e_{1}, , e_{n}) $ and $ (d_{1}, , d_{m()}) $, respectively. At each output time \(i\), compute the attention vector \(d_i\) to be linear combination of $ (e_{1}, , e_{n}) $ with weights $ (a_{1}^{i}, , a_{n}^{i}) $ \[ d_{i} = \sum_{j=1}^{n} a_{j}^{i} e_{j} \]
$ (a_{1}^{i}, , a_{n}^{i}) $ is softmax value of $ (u_{1}^{i}, , u_{n}^{i}) $ and \(u_{j}^{i}\) can be considered as distance between \(d_{i}\) and \(e_{j}\). Notice that \(v\), \(W_1\), and \(W_2\) are learnable parameters of the model.\[ \begin{eqnarray} u_{j}^{i} &=& v^{T} \tanh \left(W_{1} e_{j}+W_{2} d_\right) \quad j \in(1, \ldots, n) \\ a_{j}^{i} &=& \operatorname{softmax}\left(u_{j}^{i}\right) \quad j \in(1, \ldots, n) \end{eqnarray} \]
Pointer Networks
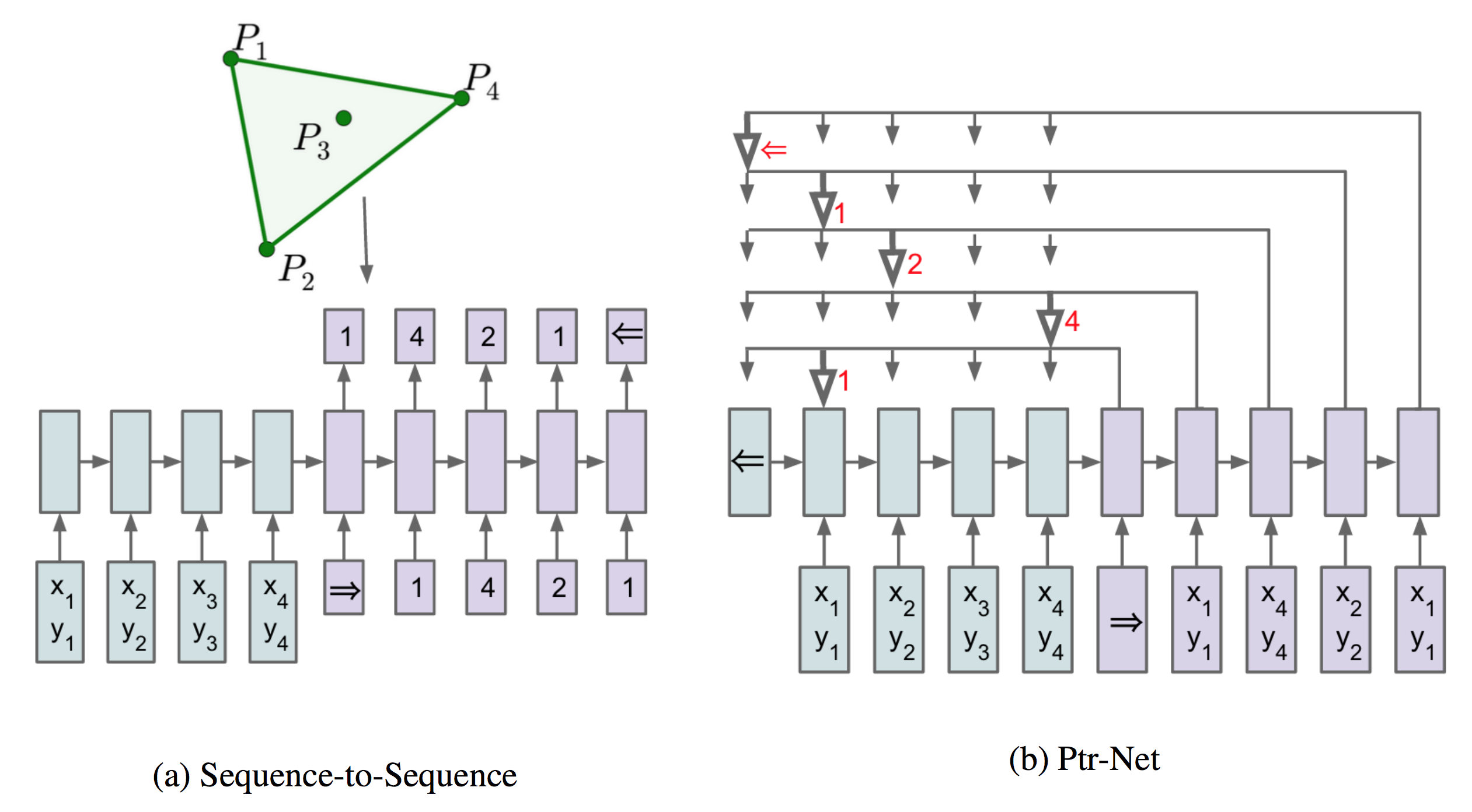
Pointer Networks does not blend the encoder state \(e_j\) to propagate extra information to the decoder, but instead, use \(u^i_j\) as pointers to the input element.
\[ \begin{eqnarray*} u_{j}^{i} &=& v^{T} \tanh \left(W_{1} e_{j}+W_{2} d_{i}\right) \quad j \in(1, \ldots, n) \\ p\left(C_{i} | C_{1}, \ldots, C_{i-1}, \mathcal{P}\right) &=& \operatorname{softmax}\left(u^{i}\right) \end{eqnarray*} \]
More on Attention
In FloydHub Blog - Attention Mechanism , a clear and detailed explanation of difference and similarity between the classic first type of Attention, commonly referred to as Additive Attention by Dzmitry Bahdanau and second classic type, known as Multiplicative Attention and proposed by Thang Luong , is discussed.
It's well known that in Luong Attention, three ways of alignment scoring function is defined, or the distance between \(d_{i}\) and \(e_{j}\).\[ \operatorname{score} \left( d_i, e_j \right)= \begin{cases} d_i^{\top} e_j & \text { dot } \\ d_i^{\top} W_a e_j & \text { general } \\ v_a^{\top} \tanh \left( W_a \left[ d_i ; e_j \right] \right) & \text { concat } \end{cases} \]
PyTorch Implementation
In episode 2, we have introduced TSP dataset where each case is a line, of following form.
1 | x0, y0, x1, y1, ... output 1 v1 v2 v3 ... 1 |
PyTorch Dataset
Each case is converted to (input, input_len, output_in, output_out, output_len) of type nd.ndarray with appropriate padding and encapsulated in a extended PyTorch Dataset.
1 | from torch.utils.data import Dataset |
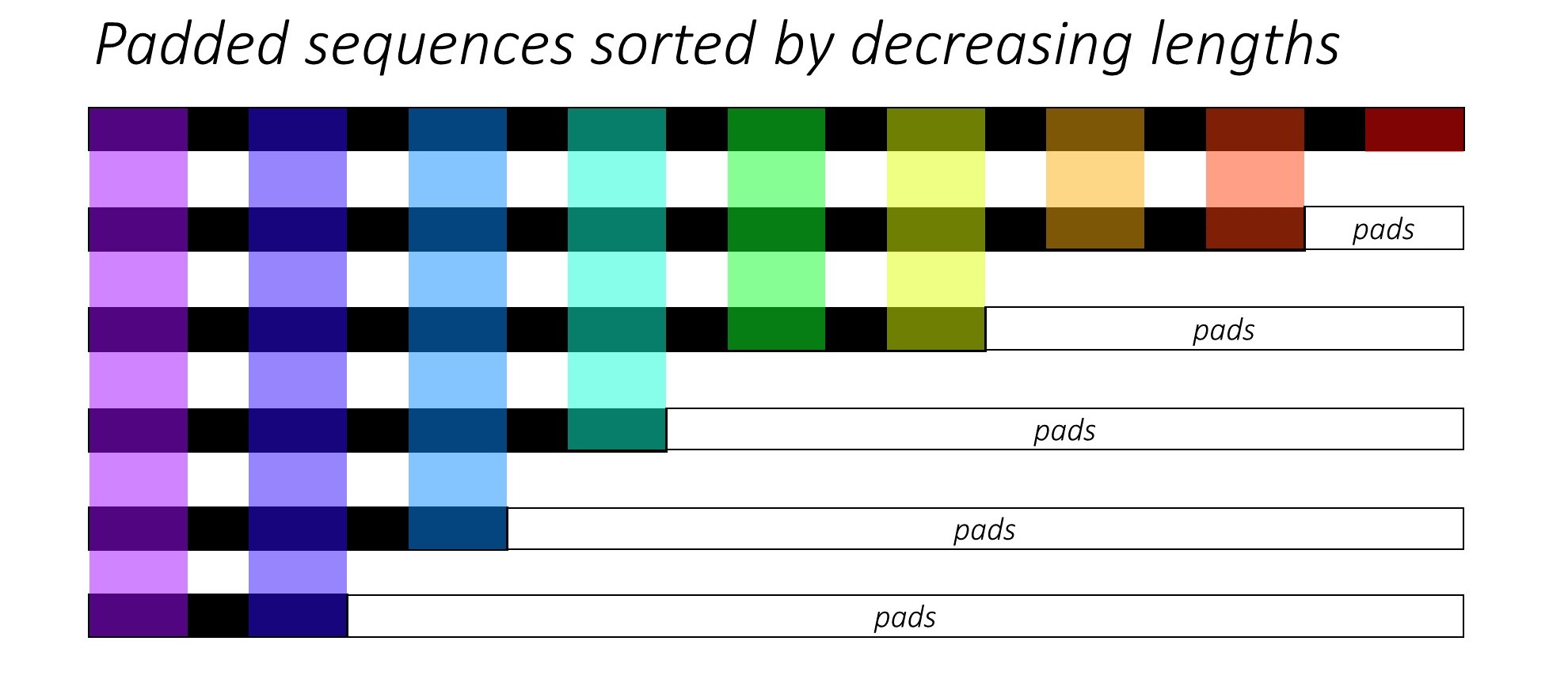
PyTorch pad_packed_sequence
Code in PyTorch seq-to-seq model typically utilizes pack_padded_sequence and pad_packed_sequence API to reduce computational cost. A detailed explanation is given here https://github.com/sgrvinod/a-PyTorch-Tutorial-to-Image-Captioning#decoder-1.
1 | class RNNEncoder(nn.Module): |
Attention Code
1 | class Attention(nn.Module): |
Complete PyTorch implementation source code is also available on github.
References
TSP From DP to Deep Learning. Episode 2: DP on Euclidean Dataset
This is second episode of series: TSP From DP to Deep Learning.
- Episode 1: AC TSP on AIZU with recursive DP
- Episode 2: TSP DP on a Euclidean Dataset
- Episode 3: Pointer Networks in PyTorch
- Episode 4: Search for Most Likely Sequence
- Episode 5: Reinforcement Learning PyTorch Implementation
AIZU TSP Bottom Up Iterative DP
In last episode, we provided a top down recursive DP in Python 3 and Java 8. Now we continue to improve and convert it to bottom up iterative DP version. Below is a graph with 3 vertices, the top down recursive calls are completely drawn.
Looking from bottom up, we could identify corresponding topological computing order with ease. First, we compute all bit states with 3 ones, then 2 ones, then 1 one.
Pseudo Java code below.
1 | for (int bitset_num = N; bitset_num >=0; bitset_num++) { |
For example, dp[00010][1] is the min distance starting from vertex 0, and just arriving at vertex 1: \(0 \rightarrow 1 \rightarrow ? \rightarrow ? \rightarrow ? \rightarrow 0\). In order to find out total min distance, we need to enumerate all possible u for first question mark. \[ (0 \rightarrow 1) + \begin{align*} \min \left\lbrace \begin{array}{r@{}l} 2 \rightarrow ? \rightarrow ? \rightarrow 0 + dist(1,2) \qquad\text{ new_state=[00110][2] } \qquad\\\\ 3 \rightarrow ? \rightarrow ? \rightarrow 0 + dist(1,3) \qquad\text{ new_state=[01010][3] } \qquad\\\\ 4 \rightarrow ? \rightarrow ? \rightarrow 0 + dist(1,4) \qquad\text{ new_state=[10010][4] } \qquad \end{array} \right. \end{align*} \]
Java Iterative DP Code
AC code in Python 3 and Java 8. Illustrate core Java code below.
1 | public long solve() { |
In this way, runtime complexity can be spotted easily, three for loops leading to O(\(2^n * n * n\)) = O(\(2^n*n^2\) ).
DP on Euclidean Dataset
So far, TSP DP has been crystal clear and we move forward to introducing PTR_NET dataset on Google Drive by Oriol Vinyals who is the author of Pointer Networks. Each line in the dataset has the following pattern:
1 | x0, y0, x1, y1, ... output 1 v1 v2 v3 ... 1 |
It first lists n points in (x, y) coordinate, followed by "output", then followed by one of the minimal distance tours, starting and ending with vertex 1 (indexed from 1 not 0).
Some examples of 10 vertices are:
1 | 0.607122 0.664447 0.953593 0.021519 0.757626 0.921024 0.586376 0.433565 0.786837 0.052959 0.016088 0.581436 0.496714 0.633571 0.227777 0.971433 0.665490 0.074331 0.383556 0.104392 output 1 3 8 6 10 9 5 2 4 7 1 |
Plot first example using code below.
1 | import matplotlib.pyplot as plt |
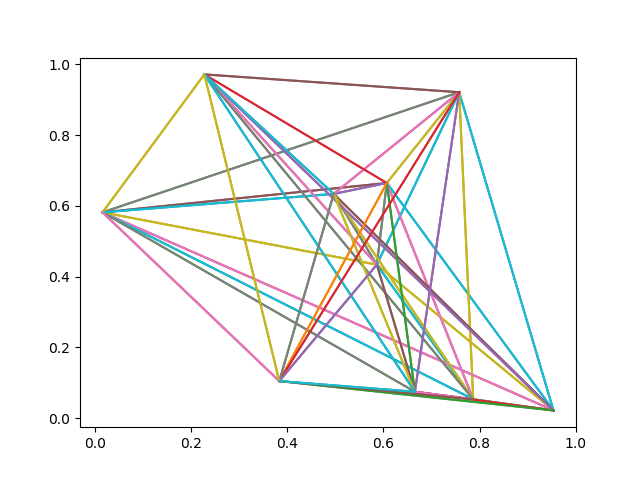
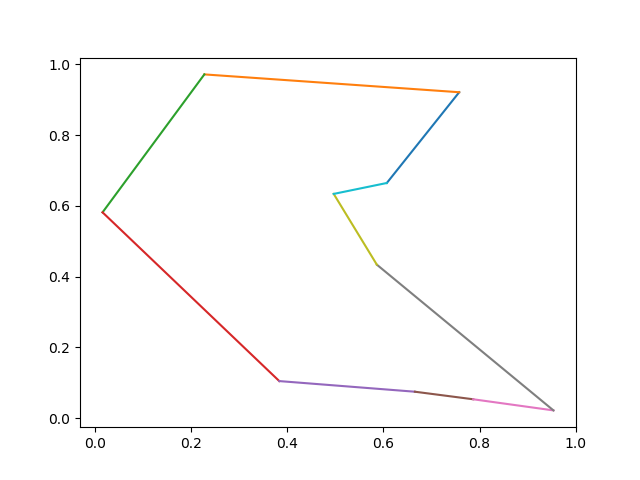
Now plot the optimal tour: \[ 1 \rightarrow 3 \rightarrow 8 \rightarrow 6 \rightarrow 10 \rightarrow 9 \rightarrow 5 \rightarrow 2 \rightarrow 4 \rightarrow 7 \rightarrow 1 \]
1 | tour_str = '1 3 8 6 10 9 5 2 4 7 1' |
Python Code Illustrated
Init Graph Edges
Based on previous top down version, several changes are made. First, we need to have an edge between every 2 vertices and due to our matrix representation of the directed edge, edges of 2 directions are initialized.
1 | g: Graph = Graph(N) |
Auxilliary Variable to Track Tour Vertices
One major enhancement is to record the optimal tour during enumerating. We introduce another variable parent[bitstate][v] to track next vertex u, with shortest path.
1 | ret: float = FLOAT_INF |
After minimal tour distance is found, one optimal tour is formed with the help of parent variable.
1 | def _form_tour(self): |
Note that for each test case, only one tour is given after "output". Our code may form a different tour but it has same distance as what the dataset generates, which can be verified by following code snippet. See full code on github.
1 | tsp: TSPSolver = TSPSolver(g) |
TSP From DP to Deep Learning. Episode 1: DP Algorithm
Travelling salesman problem (TSP) is a classic NP hard computer algorithmic problem. In this series, we will first solve TSP problem in an exact manner by ACing TSP on aizu with dynamic programming, and then move on to train a Pointer Network with Pytorch to obtain an approximate solution with deep learning and reinforcement learning technology. Complete episodes are listed as follows:
Episode 1: AC TSP on AIZU with recursive DP
Episode 2: TSP DP on a Euclidean Dataset
Episode 3: Pointer Networks in PyTorch
Episode 4: Search for Most Likely Sequence
TSP Problem Review
TSP can be modelled as a graph problem where both directed and undirected graphs and both completely or partially connected graphs are applicable. The following picture in Wikipedia TSP is an undirected but complete TSP with four vertices, A, B, C, D. TSP requries a tour with minimal total distance, starting from arbitrarily picked vertex and ending with the same node while covering all vertices exactly once. For example, \(A \rightarrow B \rightarrow C \rightarrow D \rightarrow A\) and \(A \rightarrow C \rightarrow B \rightarrow D \rightarrow A\) are valid tours and among all tours there is only one minimal distance value (though multiple tours with same minimum may exist).
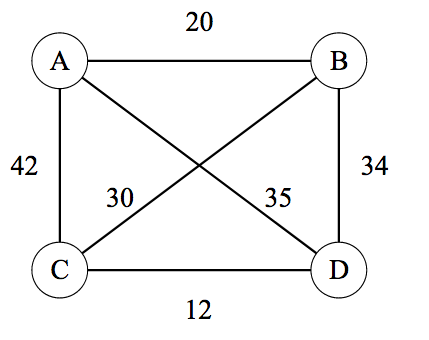
\[ \begin{matrix} & \begin{matrix}A&B&C&D\end{matrix} \\ \begin{matrix}A\\B\\C\\D\end{matrix} & \begin{bmatrix}-&20&42&35\\20&-&30&34\\42&30&-&12\\35&34&12&-\end{bmatrix}\\ \end{matrix} \]
Of course, typically, TSP problem takes the form of n cooridanates in a plane, corresponding to complete and undirected graph, because in plane every pair of vertices has one connected edge and the edge has same distance in both directions.
AIZU TSP Online Judge
AIZU has a TSP problem where a directed and incomplete graph with V vertices and E directed edges is given, and the output expects minimal total distance. For example below having 4 vertices and 6 edges.
This test case has minimal tour distance 16, with corresponding tour being \(0\rightarrow1\rightarrow3\rightarrow2\rightarrow0\), as shown in red edges. However, the AIZU problem may not have a valid result because not every pair of vertices is guaranteed to be connected. In that case, -1 is required, which can also be interpreted as infinity.
Brute Force Solution
A naive way is to enumerate all possible routes starting from vertex 0 and keep minimal total distance ever generated. Python code below illustrates a 4 point vertices graph.
1 | from itertools import permutations |
The possible routes are
1 | [0, 1, 2, 3, 0] |
Dynamic Programming
To AC AIZU TSP, we need to have acceleration of the factorial runtime complexity by using bitmask dynamic programming. First, let us map visited state to a binary value. In the 4 vertices case, it's "0110" if node 2 and 1 already visited and ending at node 1. Besides, we need to track current vertex to start from. So we extend dp from one dimension to two dimensions \(dp[bitstate][v]\). In the example, it's \(dp["0110"][1]\). The transition formula is given by \[ dp[bitstate][v] = \min ( dp[bitstate \cup \{u\}][u] + dist(v,u) \mid u \notin bitstate ) \]
The resulting time complexity is O(\(n^2*2^n\) ), since there are \(2^n * n\) total states and for each state one more round loop is needed. Factorial and exponential functions are significantly different.
| \(n!\) | \(n^2*2^n\) | |
|---|---|---|
| n=8 | 40320 | 16384 |
| n=10 | 3628800 | 102400 |
| n=12 | 479001600 | 589824 |
| n=14 | 87178291200 | 3211264 |
Pause a second and think about why bitmask DP works here. Notice there are lots of redundant sub calls, one of which is hightlighted in red ellipse below.
In this episode, a straightforward top down memoization DP version is given in Python 3 and Java 8. Benefit of top down DP approach is that we don't need to consider topological ordering when permuting all states. Notice that there is a trick in Java, where each element of dp is initialized as Integer.MAX_VALUE, so that only one statement is needed to update new dp value.
1 | res = Math.min(res, s + g.edges[v][u]); |
1 | INT_INF = -1 |
Below is complete AC code in Python 3 and Java 8. Also can be downloaded on github.
AIZU Java 8 Recursive Version
1 | // passed http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=DPL_2_A |
AIZU Python 3 Recursive Version
1 | from typing import List |