上一期 MyEncyclopedia公众号文章 从Q-Learning 演化到 DQN，我们从原理上讲解了DQN算法，这一期，让我们通过代码来实现任天堂游戏机中经典的超级玛丽的自动通关吧。本文所有代码在 https://github.com/MyEncyclopedia/reinforcement-learning-2nd/tree/master/super_mario。

DQN 算法回顾

上期详细讲解了DQN中的两个重要的技术：Target Network 和 Experience Replay，正是有了它们才使得 Deep Q Network在实战中容易收敛，以下是Deepmind 发表在Nature 的 Human-level control through deep reinforcement learning 的完整算法流程。

超级玛丽 NES OpenAI 环境

安装基于OpenAI gym的超级玛丽环境执行下面的 pip 命令即可。

1

pip install gym-super-mario-bros

我们先来看一下游戏环境的输入和输出。下面代码采用随机的action来和游戏交互。有了 组合游戏系列3: 井字棋、五子棋的OpenAI Gym GUI环境 对于OpenAI Gym 接口的介绍，现在对于其基本的交互步骤已经不陌生了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

import gym_super_mario_bros
from random import random, randrange
from gym_super_mario_bros.actions import RIGHT_ONLY
from nes_py.wrappers import JoypadSpace
from gym import wrappers

env = gym_super_mario_bros.make('SuperMarioBros-v0')
env = JoypadSpace(env, RIGHT_ONLY)

# Play randomly
done = False
env.reset()

step = 0
while not done:
    action = randrange(len(RIGHT_ONLY))
    state, reward, done, info = env.step(action)
    print(done, step, info)
    env.render()
    step += 1

env.close()

游戏render效果如下

。。。

注意我们在游戏环境初始化的时候用了参数 RIGHT_ONLY，它定义成五种动作的list，表示仅使用右键的一些组合，适用于快速训练来完成Mario第一关。

1
2
3
4
5
6
7

RIGHT_ONLY = [
    ['NOOP'],
    ['right'],
    ['right', 'A'],
    ['right', 'B'],
    ['right', 'A', 'B'],
]

观察一些 info 输出内容，coins表示金币获得数量，flag_get 表示是否取得最后的旗子，time 剩余时间，以及 Mario 大小状态和所在的 x，y位置。

1
2
3
4
5
6
7
8
9
10
11
12

{
   "coins":0,
   "flag_get":False,
   "life":2,
   "score":0,
   "stage":1,
   "status":"small",
   "time":381,
   "world":1,
   "x_pos":594,
   "y_pos":89
}

游戏图像处理

Deep Reinforcement Learning 一般是 end-to-end learning，意味着游戏的 screen image 作为observation直接视为真实状态，喂给神经网络训练。于此相反的另一种做法是，通过游戏环境拿到内部状态，例如所有相关物品的位置和属性作为模型输入。这两种方式的区别有两点。第一点，用观察到的屏幕像素代替真正的状态 s，在partially observable 的环境时可能因为 non-stationarity 导致无法很好的工作，而拿内部状态利用了额外的作弊信息，在partially observable环境中也可以工作。第二点，第一种方式屏幕像素维度比较高，输入数据量大，需要神经网络的大量训练拟合，第二种方式，内部真实状态往往维度低得多，训练起来很快，但缺点是因为除了内部状态往往还需要游戏相关规则作为输入，因此generalization能力不如前者强。

这里，我们当然采样屏幕像素的 end-to-end 方式了，自然首要任务是将游戏帧图像有效处理。超级玛丽游戏环境的屏幕输出是 (240, 256, 3) shape的 numpy array，通过下面一系列的转换，尽可能的在不影响训练效果的情况下减小采样到的数据量。

1. MaxAndSkipFrameWrapper：每4个frame连在一起，采取同样的动作，降低frame数量。

2. FrameDownsampleWrapper：将原始的 (240, 256, 3) down sample 到 (84, 84, 1)

3. ImageToPyTorchWrapper：转换成适合 pytorch 的 (1, 84, 84) shape

4. FrameBufferWrapper：保存最后4次屏幕采样

5. NormalizeFloats：Normalize 成 [0., 1.0] 的浮点值

1
2
3
4
5
6
7
8
9

def wrap_environment(env_name: str, action_space: list) -> Wrapper:
    env = make(env_name)
    env = JoypadSpace(env, action_space)
    env = MaxAndSkipFrameWrapper(env)
    env = FrameDownsampleWrapper(env)
    env = ImageToPyTorchWrapper(env)
    env = FrameBufferWrapper(env, 4)
    env = NormalizeFloats(env)
    return env

CNN 模型

模型比较简单，三个卷积层后做 softmax输出，输出维度数为离散动作数。act() 采用了epsilon-greedy 模式，即在epsilon小概率时采取随机动作来 explore，大于epsilon时采取估计的最可能动作来 exploit。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class DQNModel(nn.Module):
    def __init__(self, input_shape, num_actions):
        super(DQNModel, self).__init__()
        self._input_shape = input_shape
        self._num_actions = num_actions

        self.features = nn.Sequential(
            nn.Conv2d(input_shape[0], 32, kernel_size=8, stride=4),
            nn.ReLU(),
            nn.Conv2d(32, 64, kernel_size=4, stride=2),
            nn.ReLU(),
            nn.Conv2d(64, 64, kernel_size=3, stride=1),
            nn.ReLU()
        )

        self.fc = nn.Sequential(
            nn.Linear(self.feature_size, 512),
            nn.ReLU(),
            nn.Linear(512, num_actions)
        )

    def forward(self, x):
        x = self.features(x).view(x.size()[0], -1)
        return self.fc(x)

    def act(self, state, epsilon, device):
        if random() > epsilon:
            state = torch.FloatTensor(np.float32(state)).unsqueeze(0).to(device)
            q_value = self.forward(state)
            action = q_value.max(1)[1].item()
        else:
            action = randrange(self._num_actions)
        return action

Experience Replay 缓存

实现采用了 Pytorch CartPole DQN 的官方代码，本质是一个最大为 capacity 的 list 保存采样的 (s, a, r, s', is_done) 五元组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Transition = namedtuple('Transition', ('state', 'action', 'reward', 'next_state', 'done'))

class ReplayMemory:

    def __init__(self, capacity):
        self.capacity = capacity
        self.memory = []
        self.position = 0

    def push(self, *args):
        if len(self.memory) < self.capacity:
            self.memory.append(None)
        self.memory[self.position] = Transition(*args)
        self.position = (self.position + 1) % self.capacity

    def sample(self, batch_size):
        return random.sample(self.memory, batch_size)

    def __len__(self):
        return len(self.memory)

DQNAgent

我们将 DQN 的逻辑封装在 DQNAgent 类中。DQNAgent 成员变量包括两个 DQNModel，一个ReplayMemory。

train() 方法中会每隔一定时间将 Target Network 的参数同步成现行Network的参数。在td_loss_backprop()方法中采样 ReplayMemory 中的五元组，通过minimize TD error方式来改进现行 Network 参数 \(\theta\)。Loss函数为：

\[ L\left(\theta_{i}\right)=\mathbb{E}_{\left(s, a, r, s^{\prime}\right) \sim \mathrm{U}(D)}\left[\left(r+\gamma \max _{a^{\prime}} Q_{target}\left(s^{\prime}, a^{\prime} ; \theta_{i}^{-}\right)-Q\left(s, a ; \theta_{i}\right)\right)^{2}\right] \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

class DQNAgent():

    def act(self, state, episode_idx):
        self.update_epsilon(episode_idx)
        action = self.model.act(state, self.epsilon, self.device)
        return action

    def process(self, episode_idx, state, action, reward, next_state, done):
        self.replay_mem.push(state, action, reward, next_state, done)
        self.train(episode_idx)

    def train(self, episode_idx):
        if len(self.replay_mem) > self.initial_learning:
            if episode_idx % self.target_update_frequency == 0:
                self.target_model.load_state_dict(self.model.state_dict())
            self.optimizer.zero_grad()
            self.td_loss_backprop()
            self.optimizer.step()

    def td_loss_backprop(self):
        transitions = self.replay_mem.sample(self.batch_size)
        batch = Transition(*zip(*transitions))

        state = Variable(FloatTensor(np.float32(batch.state))).to(self.device)
        action = Variable(LongTensor(batch.action)).to(self.device)
        reward = Variable(FloatTensor(batch.reward)).to(self.device)
        next_state = Variable(FloatTensor(np.float32(batch.next_state))).to(self.device)
        done = Variable(FloatTensor(batch.done)).to(self.device)

        q_values = self.model(state)
        next_q_values = self.target_net(next_state)

        q_value = q_values.gather(1, action.unsqueeze(-1)).squeeze(-1)
        next_q_value = next_q_values.max(1)[0]
        expected_q_value = reward + self.gamma * next_q_value * (1 - done)

        loss = (q_value - expected_q_value.detach()).pow(2)
        loss = loss.mean()
        loss.backward()

外层 Training 代码

最后是外层调用代码，基本和以前文章一样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

def train(env, args, agent):
    for episode_idx in range(args.num_episodes):
        episode_reward = 0.0
        state = env.reset()

        while True:
            action = agent.act(state, episode_idx)
            if args.render:
                env.render()
            next_state, reward, done, stats = env.step(action)
            agent.process(episode_idx, state, action, reward, next_state, done)
            state = next_state
            episode_reward += reward
            if done:
                print(f'{episode_idx}: {episode_reward}')
                break

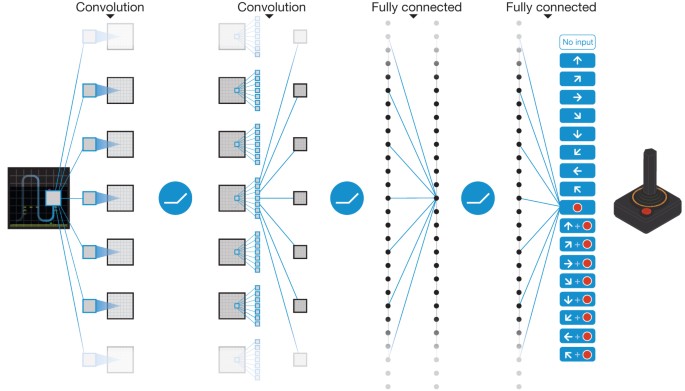
上一期 MyEncyclopedia公众号文章 SARSA、Q-Learning和Expected SARSA时序差分算法训练CartPole中，我们通过CartPole的OpenAI Gym环境实现了Q-learning算法，这一期，我们将会分析Q-learning算法面临的maximization bias 问题和提出double learning算法来改进。接着，我们将tabular Q-learning算法扩展到用带参函数来近似 Q(s, a)，这就是Deepmind 在2015年Nature上发表的Deep Q Network （DQN）思想：用神经网络结合Q-learning算法实现超越人类玩家打Atari游戏的水平。

Q-Learning 回顾

在SARSA、Q-Learning和Expected SARSA时序差分算法训练CartPole 中，我们实现了同样基于 \(\epsilon\)-greedy 策略的Q-learning算法和SARSA算法，两者代码上的区别确实不大，但本质上Q-learning是属于 off-policy 范畴而 SARSA却属于 on-policy 范畴。一种理解方式是，Q-learning相比于SARSA少了第二次从 \(\epsilon\)-greedy 策略采样出下一个action，即S, A, R', S', A' 五元组中最后一个A'，而直接通过max操作去逼近 \(q^{*}\)。如此，Q-learning并没有像SARSA完成一次完整的GPI（Generalized Policy Iteration），缺乏on-policy的策略迭代的特点，故而 Q-learning 属于off-policy方法。我们也可以从另一个角度来分析两者的区别。注意到这两个算法不是一定非要使用 \(\epsilon\)-greedy 策略的。对于Q-learning来说，完全可以使用随机策略，理论上已经证明，只要保证每个action以后依然有几率会被探索下去，Q-learning 最终会收敛到最优策略。Q-learning使用 \(\epsilon\)-greedy 是为了能快速收敛。对于SARSA算法来说，则无法使用随机策略，因为随机策略无法形成策略提升。而 \(\epsilon\)-greedy 策略却可以形成策略迭代，完成策略提升，当然，\(\epsilon\)-greedy 策略在 SARSA 算法中也可以保证快速收敛。因此，尽管两者都使用 \(\epsilon\)-greedy 策略再借由环境产生reward和state，它们的作用并非完全一样。至此，我们可以体会到on-policy和off-policy本质的区别。

收敛条件

一种方式是将 \(\alpha\)设置成 (s, a)访问次数的倒数：\(\alpha_{n}(s,a) = 1/ n(s,a )\)

则整体更新公式为

\[ Q(s,a) \leftarrow Q(s,a) + \alpha_n(s, a)[R+\gamma \max_{a^{\prime}}Q(s^{\prime}, a^{\prime}) - Q(s, a)] \]

Q-Learning 最大化偏差问题

Q-Learning 会产生最大化偏差问题（Maximization Bias，在Sutton 教材6.7节），它的原因是用估计值中取最大值去估计真实值中最大是有偏的。这个可以做如下试验来模拟，若有5个 [-3, 3] 的离散均匀分布 \(d_i\)，\(\max(\mathbb{E}[d_i]) = 0\)，但是若我们用单批采样 \(x_i \sim d_i\)来估算 \(\mathbb{E}[d_i]\)在取max的话，\(\mathbb{E}[{\max(x_i)]}\) 是有bias的。但是如果我们将这个过程分解成选择最大action和评估其值两步，每一步用独立的采样集合就可以做到无偏，这个改进方法称为double learning。具体过程为第一步在\(Q_1\)集合中找到最大的action，第二步在\(Q_2\)中返回此action值，即：

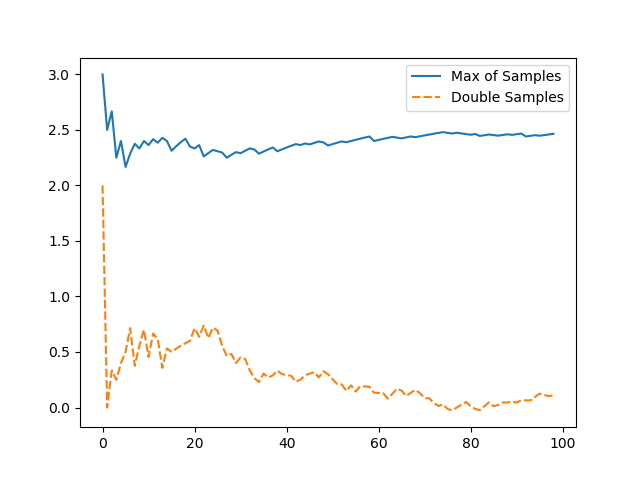
则无限模拟后结果是无偏的：\(\mathbb{E}[Q_2(A^{\star})] = q(A^{\star})\) 下面是简单模拟试验两种方法的均值比较

试验完整代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

import random
from math import floor
import numpy as np
import pandas as pd
import seaborn as sns


def uniform(a: int, b: int) -> int:
    u = random.random()
    return a + floor((b - a + 1) * u)


if __name__ == "__main__":
    total_max_bias = 0
    avgs_max_bias = []
    total_double_sampling = 0
    avgs_double_sampling = []

    for e in range(1, 100):
        samples = np.array([uniform(-3, 3) for _ in range(5)])
        max_sample = max(samples)
        total_max_bias += max_sample
        avgs_max_bias.append(total_max_bias / e)

        samples2 = np.array([uniform(-3, 3) for _ in range(5)])
        total_double_sampling += samples2[np.argmax(samples)]
        avgs_double_sampling.append(total_double_sampling / e)

    df = pd.DataFrame({'Max of Samples': avgs_max_bias, 'Double Samples': avgs_double_sampling})
    import matplotlib.pyplot as plt
    sns.lineplot(data=df)
    plt.show()

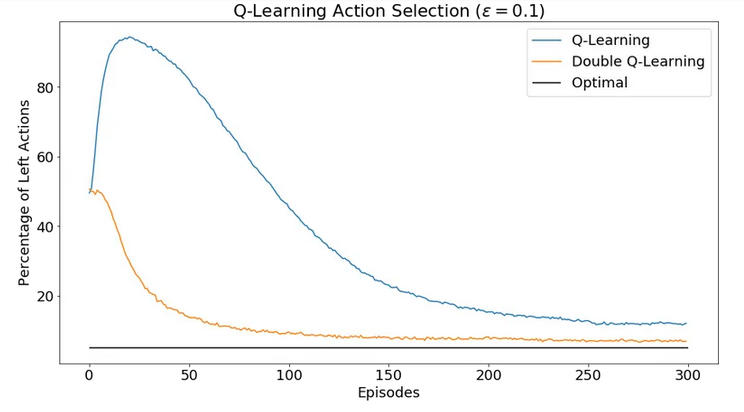
回到Q-learning 中使用的 \(\epsilon\)-greedy策略，Q-learning可以保证随着\(\epsilon\) 的减小，最大化偏差会 asymptotically 趋近于真实值，但是double learning 可以更快地趋近于真实值。

下面是Sutton 强化学习第二版6.7节中完整的Double Q-learning算法。

更详细内容，可以参考 Hado V. Hasselt 的 Double Q-learning paper [3]。

Gradient Q-Learning

Tabular Q-learning由于受制于维度爆炸，无法扩展到高维状态空间，一般近似解决方案是用 approximating function来逼近Q函数。即我们将状态抽象出一组特征 \(s = \vec x= [x_1, x_2, ..., x_n]^T\)，Q 用一个 x 的函数来近似表达 \(Q(s, a) \approx g(\vec x; \theta)\)，如此，就联系起了深度神经网络。有了函数表达，深度学习还必须的元素是损失函数，这个很自然的可以用 TD error。至此，问题转换成深度学习的几个要素均已具备，Q-learning算法改造成了深度学习中的有监督问题。

估计值：\(Q\left(s, a ; \theta\right)\)

目标值：\(r+\gamma \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime} ; \theta\right)\)

损失函数：

\[ L\left(\theta\right)=\mathbb{E}_{\left(s, a, r, s^{\prime}\right) \sim \mathrm{U}(D)}\left[\left(r+\gamma \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime} ; \theta\right)-Q\left(s, a ; \theta\right)\right)^{2}\right] \]

收敛性分析

首先明确一点，至此 gradient q-learning 和 tabular Q-learning 一样，都是没有记忆的，即对于一个新的环境产生的 sample 去做 stochastic online update。

若Q函数是状态特征的线性函数，即 \(Q(s, a; \theta) = \Sigma_i w_i x_i\) ，那么线性Gradient Q-learning的收敛条件和Tabular Q-learning 一样，也为

若Q函数是非线性函数，即使符合上述条件，也无法保证收敛，本质上源于改变 \(\theta\) 使得 Q 值在 (s, a) 点上减小误差会影响 (s, a) 周边点的误差。

DQN减少不收敛的两个技巧

1. \(\theta_{i-1} \rightarrow \theta_{i}\) 改变导致max中的估计值和目标值中的Q同时变化，面临着 chasing its own tail 的问题。解决的方法是使用不同的参数来parameterize两个Q，并且目标值的Q网络参数固定一段时间产生一批固定策略下的环境采样。这个技巧称为 Target Network。引入这个 trick 后深度学习的要素变成

估计值：\(Q\left(s, a ; \theta_{i}\right)\)

目标值：\(r+\gamma \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime} ; \theta_i^{-}\right)\)

损失函数，DQN在Nature上的loss函数： \[ L\left(\theta_{i}\right)=\mathbb{E}_{\left(s, a, r, s^{\prime}\right) \sim \mathrm{U}(D)}\left[\left(r+\gamma \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime} ; \theta_{i}^{-}\right)-Q\left(s, a ; \theta_{i}\right)\right)^{2}\right] \]

2. 尽管目标值的 \(Q(;\theta^{-})\)固定了，但是\(\theta_{i-1} \rightarrow \theta_{i}\) 还会使得估计值的 \(Q(s, a;\theta_i)\) 在变化的同时影响其他的 \(Q(s_k, a_j;\theta_i)\)，让之前训练过的 (s, a)的点的损失值发生变化，解决的办法是将 online stochastic 改成 batch gradient，也就是将最近的一系列采样值保存下来，这个方法称为 experience replay。

有了这两个优化，Deep Q Network投入实战效果就容易收敛了，以下是Deepmind 发表在Nature 的 Human-level control through deep reinforcement learning [1] 的完整算法流程。

DQN with Double Q-Learning

DQN 算法和 Double Q-Learning 能不能结合起来呢？Hado van Hasselt 在 Deep Reinforcement Learning with Double Q-learning [4] 中提出参考 Double Q-learning 将 DQN 的目标值改成如下函数，可以进一步提升最初DQN的效果。

目标值：\(r+\gamma Q(s^{\prime}, \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime}; \theta_t\right); \theta_t^{-})\)

参考资料

1. Human-level control through deep reinforcement learning Volodymyr Mnih, Koray Kavukcuoglu, David Silver (2015)

2. CS885 Reinforcement Learning Lecture 4b: May 11, 2018

3. Double Q-learning Hado V. Hasselt (2010)

4. Deep Reinforcement Learning with Double Q-learning Hado van Hasselt, Arthur Guez, David Silver (2015)