上一篇我们从原理层面解析了AlphaGo Zero如何改进MCTS算法，通过不断自我对弈，最终实现从零棋力开始训练直至能够打败任何高手。在本篇中，我们在已有的N子棋OpenAI Gym 环境中用Pytorch实现一个简化版的AlphaGo Zero算法。本篇所有代码在 github MyEncyclopedia/ConnectNGym 中，其中部分参考了SongXiaoJun 的 AlphaZero_Gomoku。

• 第一篇: Leetcode中的Minimax 和 Alpha Beta剪枝

• 第二篇: 井字棋Leetcode系列题解和Minimax最佳策略实现

• 第三篇: 井字棋、五子棋的OpenAI Gym GUI环境

• 第四篇: AlphaGo Zero 强化学习算法原理深度分析

• 第五篇: 井字棋、五子棋AlphaGo Zero 算法实战

AlphaGo Zero MCTS 树节点

上一篇中，我们知道AlphaGo Zero 的MCTS树搜索是基于传统MCTS 的UCT （UCB for Tree）的改进版PUCT（Polynomial Upper Confidence Trees）。局面节点的PUCT值由两部分组成，分别是代表Exploitation的action value Q值，和代表Exploration的U值。 \[ PUCT(s, a) =Q(s,a) + U(s,a) \] U值计算由这些参数决定：系数\(c_{puct}\)，节点先验概率P(s, a) ，父节点访问次数，本节点的访问次数。具体公式如下 \[ U(s, a)=c_{p u c t} \cdot P(s, a) \cdot \frac{\sqrt{\Sigma_{b} N(s, b)}}{1+N(s, a)} \]

因此在实现过程中，对于一个树节点来说，需要保存其Q值、节点访问次数 _visit_num和先验概率 _prior。其中，_prior在节点初始化后不变，Q值和 visit_num随着游戏MCTS模拟进程而改变。此外，节点保存了 parent和_children变量，用于维护父子关系。c_puct为class variable，作为全局参数。

1
2
3
4
5
6
7
8
9
10
11
12

class TreeNode:
    """
    MCTS Tree Node
    """

    c_puct: ClassVar[int] = 5  # class-wise global param c_puct, exploration weight factor.

    _parent: TreeNode
    _children: Dict[int, TreeNode]  # map from action to TreeNode
    _visit_num: int
    _Q: float   # Q value of the node, which is the mean action value.
    _prior: float

和上面的计算公式相对应，下列代码根据节点状态计算PUCT(s, a)。

1
2
3
4
5
6
7
8
9
10

class TreeNode:

    def get_puct(self) -> float:
        """
        Computes AlphaGo Zero PUCT (polynomial upper confidence trees) of the node.

        :return: Node PUCT value.
        """
        U = (TreeNode.c_puct * self._prior * np.sqrt(self._parent._visit_num) / (1 + self._visit_num))
        return self._Q + U

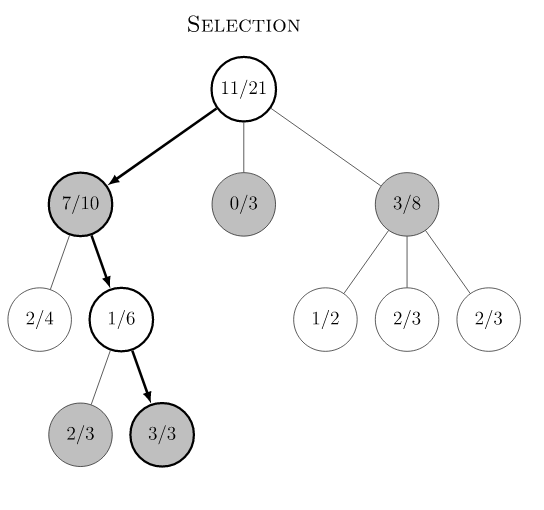
AlphaGo Zero MCTS在playout时遇到已经被展开的节点，会根据selection规则选择子节点，该规则本质上是在所有子节点中选择最大的PUCT值的节点。

\[ a=\operatorname{argmax}_a(PUCT(s, a))=\operatorname{argmax}_a(Q(s,a) + U(s,a)) \]

1
2
3
4
5
6
7
8
9

class TreeNode:

    def select(self) -> Tuple[Pos, TreeNode]:
        """
        Selects an action(Pos) having max UCB value.

        :return: Action and corresponding node
        """
        return max(self._children.items(), key=lambda act_node: act_node[1].get_puct())

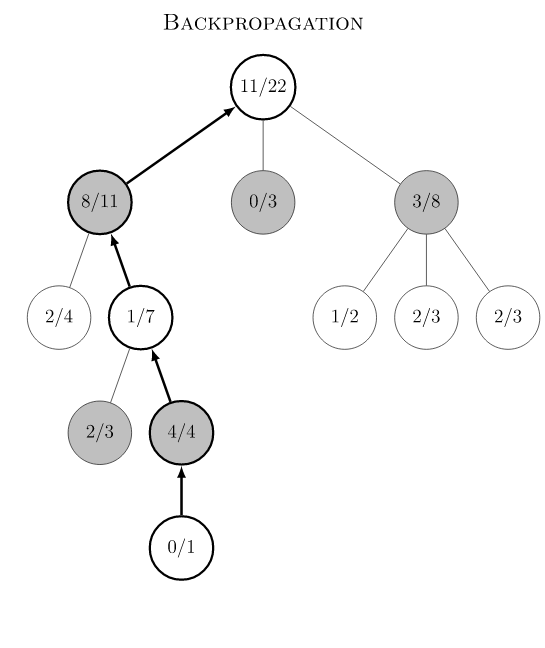
新的叶节点一旦在playout时产生，关联的 v 值会一路向上更新至根节点，具体新节点的v值将在下一节中解释。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class TreeNode:

    def propagate_to_root(self, leaf_value: float):
        """
        Updates current node with observed leaf_value and propagates to root node.

        :param leaf_value:
        :return:
        """
        if self._parent:
            self._parent.propagate_to_root(-leaf_value)
        self._update(leaf_value)

    def _update(self, leaf_value: float):
        """
        Updates the node by newly observed leaf_value.

        :param leaf_value:
        :return:
        """
        self._visit_num += 1
        # new Q is updated towards deviation from existing Q
        self._Q += 0.5 * (leaf_value - self._Q)

AlphaGo Zero MCTS Player 实现

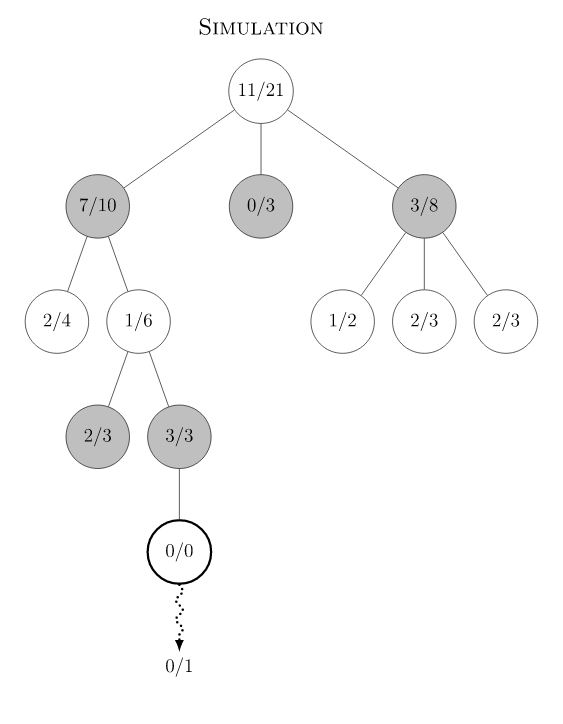
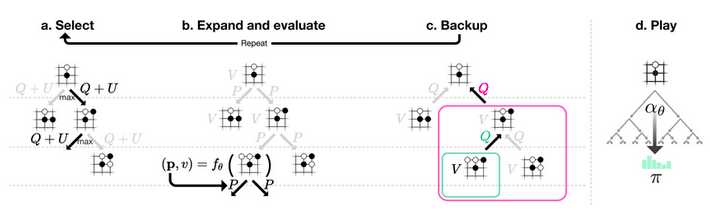
AlphaGo Zero MCTS 在训练阶段分为如下几个步骤。游戏初始局面下，整个局面树的建立由子节点的不断被探索而丰富起来。AlphaGo Zero对弈一次即产生了一次完整的游戏开始到结束的动作系列。在对弈过程中的某一游戏局面，需要采样海量的playout，又称MCTS模拟，以此来决定此局面的下一步动作。一次playout可视为在真实游戏状态树的一种特定采样，playout可能会产生游戏结局，生成真实的v值；也可能explore 到新的叶子节点，此时v值依赖策略价值网络的输出，目的是利用训练的神经网络来产生高质量的游戏对战局面。每次playout会从当前给定局面递归向下，向下的过程中会遇到下面三种节点情况。

• 若局面节点是游戏结局（叶子节点），可以得到游戏的真实价值 z。从底部节点带着z向上更新沿途节点的Q值，直至根节点（初始局面）。
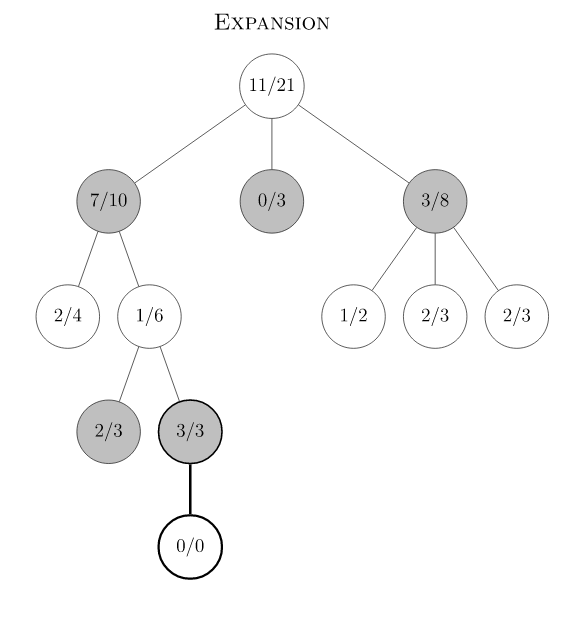
• 若局面节点从未被扩展过（叶子节点），此时会将局面编码输入到策略价值双头网络，输出结果为网络预估的action分布和v值。Action分布作为节点先验概率P(s, a)来初始化子节点，预估的v值和上面真实游戏价值z一样，从叶子节点向上沿途更新到根节点。
• 若局面节点已经被扩展过，则根据PUCT的select规则继续选择下一节点。

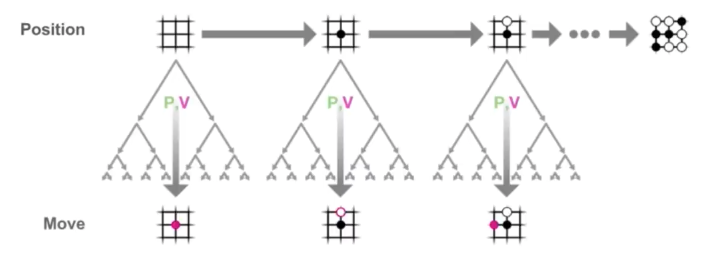
海量的playout模拟后，建立了游戏状态树的节点信息。但至此，AI玩家只是收集了信息，还仍未给定局面落子，而落子的决定由Play规则产生。下图展示了给定局面（Current节点）下，MCST模拟进行的多次playout探索后生成的局面树，play规则根据这些节点信息，产生Current 节点的动作分布 \(\pi\) ，确定下一步落子。

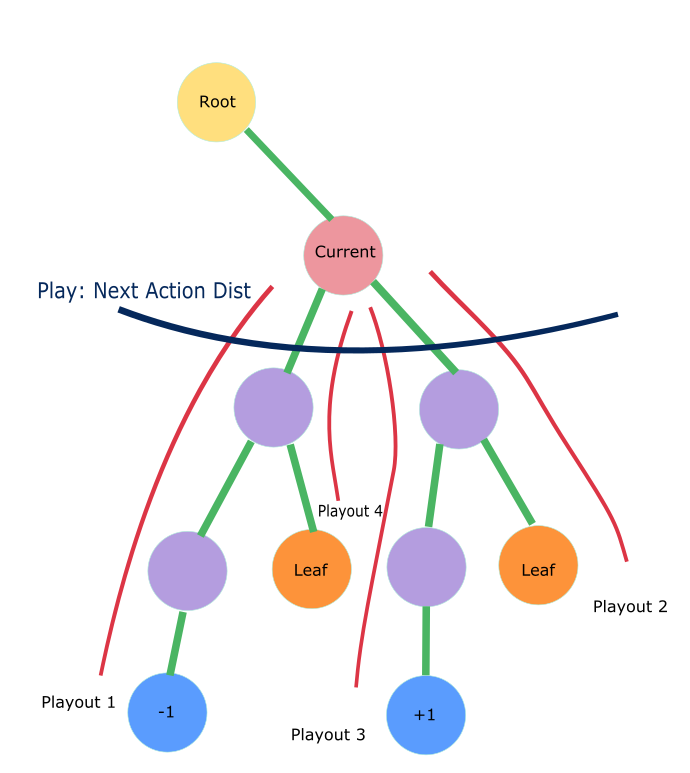
Play 给定局面

对于当前需要做落子决定的某游戏局面\(s_0\)，根据如下play公式生成落子分布 $$ ，子局面的落子概率正比于其访问次数的某次方。其中，某次方的倒数称为温度参数（Temperature）。

\[ \pi\left(a \mid s_{0}\right)=\frac{N\left(s_{0}, a\right)^{1 / \tau}}{\sum_{b} N\left(s_{0}, b\right)^{1 / \tau}} \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

class MCTSAlphaGoZeroPlayer(BaseAgent):

    def _next_step_play_act_probs(self, game: ConnectNGame) -> Tuple[List[Pos], ActionProbs]:
        """
        For the given game status, run playouts number of times specified by self._playout_num.
        Returns the action distribution according to AlphaGo Zero MCTS play formula.

        :param game:
        :return: actions and their probability
        """

        for n in range(self._playout_num):
            self._playout(copy.deepcopy(game))

        act_visits = [(act, node._visit_num) for act, node in self._current_root._children.items()]
        acts, visits = zip(*act_visits)
        act_probs = softmax(1.0 / MCTSAlphaGoZeroPlayer.temperature * np.log(np.array(visits) + 1e-10))

        return acts, act_probs

在训练模式时，考虑到偏向exploration的目的，在\(\pi\) 落子分布的基础上增加了 Dirichlet 分布。

\[ P(s,a) = (1-\epsilon)*\pi(a \mid s) + \epsilon * \boldsymbol{\eta} \quad (\boldsymbol{\eta} \sim \operatorname{Dir}(0.3)) \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

class MCTSAlphaGoZeroPlayer(BaseAgent):

    def get_action(self, board: PyGameBoard) -> Pos:
        """
        Method defined in BaseAgent.

        :param board:
        :return: next move for the given game board.
        """
        return self._get_action(copy.deepcopy(board.connect_n_game))[0]

    def _get_action(self, game: ConnectNGame) -> Tuple[MoveWithProb]:
        epsilon = 0.25
        avail_pos = game.get_avail_pos()
        move_probs: ActionProbs = np.zeros(game.board_size * game.board_size)
        assert len(avail_pos) > 0

        # the pi defined in AlphaGo Zero paper
        acts, act_probs = self._next_step_play_act_probs(game)
        move_probs[list(acts)] = act_probs
        if self._is_training:
            # add Dirichlet Noise when training in favour of exploration
            p_ = (1-epsilon) * act_probs + epsilon * np.random.dirichlet(0.3 * np.ones(len(act_probs)))
            move = np.random.choice(acts, p=p_)
            assert move in game.get_avail_pos()
        else:
            move = np.random.choice(acts, p=act_probs)

        self.reset()
        return move, move_probs

一次完整的对弈

一次完整的AI对弈就是从初始局面迭代play直至游戏结束，对弈生成的数据是一系列的 $(s, , z) $。

如下图 s0 到 s5 是某次井字棋的对弈。最终结局是先手黑棋玩家赢，即对于黑棋玩家 z = +1。需要注意的是：z = +1 是对于所有黑棋面临的局面，即s0, s2, s4，而对应的其余白棋玩家来说 z = -1。

以下代码展示如何在AI对弈时收集数据 $(s, , z) $

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class MCTSAlphaGoZeroPlayer(BaseAgent):

    def self_play_one_game(self, game: ConnectNGame) \
            -> List[Tuple[NetGameState, ActionProbs, NDArray[(Any), np.float]]]:
        """

        :param game:
        :return:
            Sequence of (s, pi, z) of a complete game play. The number of list is the game play length.
        """

        states: List[NetGameState] = []
        probs: List[ActionProbs] = []
        current_players: List[np.float] = []

        while not game.game_over:
            move, move_probs = self._get_action(game)
            states.append(convert_game_state(game))
            probs.append(move_probs)
            current_players.append(game.current_player)
            game.move(move)

        current_player_z = np.zeros(len(current_players))
        current_player_z[np.array(current_players) == game.game_result] = 1.0
        current_player_z[np.array(current_players) == -game.game_result] = -1.0
        self.reset()

        return list(zip(states, probs, current_player_z))

Playout 代码实现

一次playout会从当前局面根据PUCT selection规则下沉到叶子节点，如果此叶子节点非游戏终结点，则会扩展当前节点生成下一层新节点，其先验分布由策略价值网络输出的action分布决定。一次playout最终会得到叶子节点的 v 值，并沿着MCTS树向上更新沿途的所有父节点 Q值。 从上一篇文章已知，游戏节点的数量随着参数而指数级增长，举例来说，井字棋（k=3，m=n=3）的状态数量是5478，k=3，m=n=4时是6035992 ，k=m=n=4时是9722011 。如果我们将初始局面节点作为根节点，同时保存海量playout探索得到的局面节点，实现时会发现我们无法将所有探索到的局面节点都保存在内存中。这里的一种解决方法是在一次self play中每轮playout之后，将根节点重置成落子的节点，从而有效控制整颗局面树中的节点数量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

class MCTSAlphaGoZeroPlayer(BaseAgent):
    
    def _playout(self, game: ConnectNGame):
        """
        From current game status, run a sequence down to a leaf node, either because game ends or unexplored node.
        Get the leaf value of the leaf node, either the actual reward of game or action value returned by policy net.
        And propagate upwards to root node.

        :param game:
        """
        player_id = game.current_player

        node = self._current_root
        while True:
            if node.is_leaf():
                break
            act, node = node.select()
            game.move(act)

        # now game state is a leaf node in the tree, either a terminal node or an unexplored node
        act_and_probs: Iterator[MoveWithProb]
        act_and_probs, leaf_value = self._policy_value_net.policy_value_fn(game)

        if not game.game_over:
            # case where encountering an unexplored leaf node, update leaf_value estimated by policy net to root
            for act, prob in act_and_probs:
                game.move(act)
                child_node = node.expand(act, prob)
                game.undo()
        else:
            # case where game ends, update actual leaf_value to root
            if game.game_result == ConnectNGame.RESULT_TIE:
                leaf_value = ConnectNGame.RESULT_TIE
            else:
                leaf_value = 1 if game.game_result == player_id else -1
            leaf_value = float(leaf_value)

        # Update leaf_value and propagate up to root node
        node.propagate_to_root(-leaf_value)

编码游戏局面

为了将信息有效的传递给策略神经网络，必须从当前玩家的角度编码游戏局面。局面不仅要反映棋盘上黑白棋子的位置，也需要考虑最后一个落子的位置以及是否为当前玩家棋局。因此，我们将某局面按照当前玩家来编码，返回类型为4个棋盘大小组成的ndarray，即shape [4, board_size, board_size]，其中

1. 第一个数组编码当前玩家的棋子位置
2. 第二个数组编码对手玩家棋子位置
3. 第三个表示最后落子位置
4. 第四个全1表示此局面为先手（黑棋）局面，全0表示白棋局面

例如之前游戏对弈中的前四步：

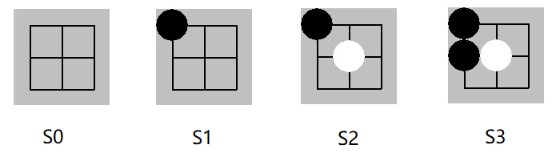
s1->s2 后局面s2的编码：当前玩家为黑棋玩家，编码局面s2 返回如下ndarray，数组[0] 为s2黑子位置，[1]为白子位置，[2]表示最后一个落子(1, 1) ，[3] 全1表示当前是黑棋落子的局面。

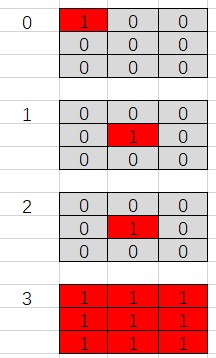
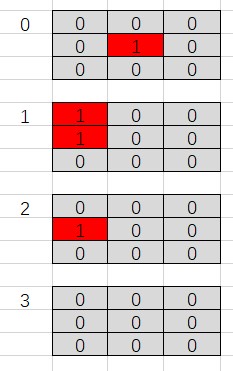
具体代码实现如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

NetGameState = NDArray[(4, Any, Any), np.int]


def convert_game_state(game: ConnectNGame) -> NetGameState:
    """
    Converts game state to type NetGameState as ndarray.

    :param game:
    :return:
        Of shape 4 * board_size * board_size.
        [0] is current player positions.
        [1] is opponent positions.
        [2] is last move location.
        [3] all 1 meaning move by black player, all 0 meaning move by white.
    """
    state_matrix = np.zeros((4, game.board_size, game.board_size))

    if game.action_stack:
        actions = np.array(game.action_stack)
        move_curr = actions[::2]
        move_oppo = actions[1::2]
        for move in move_curr:
            state_matrix[0][move] = 1.0
        for move in move_oppo:
            state_matrix[1][move] = 1.0
        # indicate the last move location
        state_matrix[2][actions[-1]] = 1.0
    if len(game.action_stack) % 2 == 0:
        state_matrix[3][:, :] = 1.0  # indicate the colour to play
    return state_matrix[:, ::-1, :]

策略价值网络训练

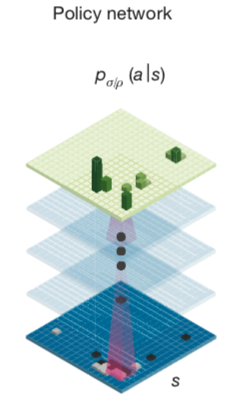
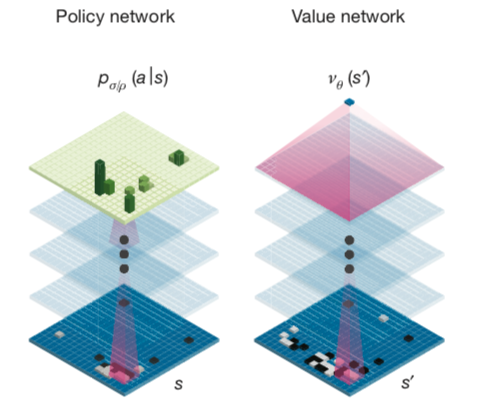
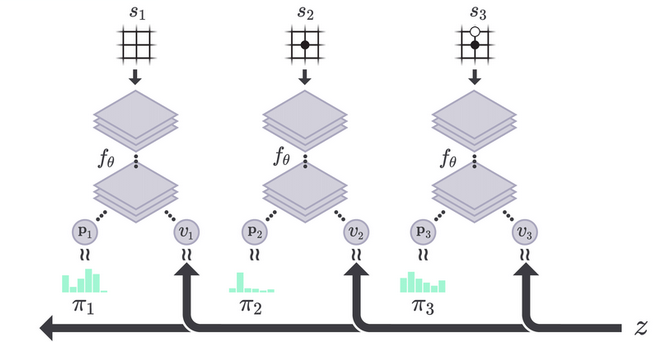
策略价值网络是一个共享参数 \(\theta\) 的双头网络，给定上面的游戏局面编码会产生预估的p和v。

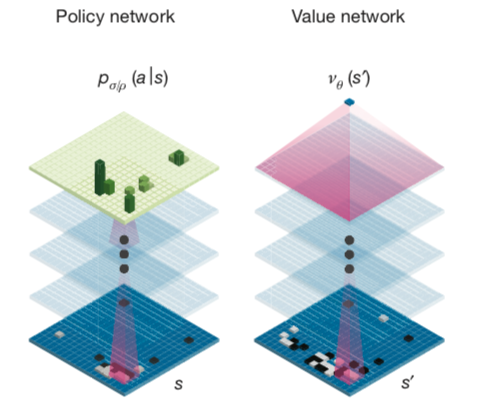
\[ \vec{p_{\theta}}, v_{\theta}=f_{\theta}(s) \] 结合真实游戏对弈后产生三元组数据 $(s, , z) $ ，按照论文中的loss 来训练神经网络。 \[ l=\sum_{t}\left(v_{\theta}\left(s_{t}\right)-z_{t}\right)^{2}-\vec{\pi_{t}} \cdot \log \left(\vec{p_{\theta}}\left(s_{t}\right)\right) + c {\lVert \theta \rVert}^2 \]

下面代码为Pytorch backward部分。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def backward_step(self, state_batch: List[NetGameState], probs_batch: List[ActionProbs],
               value_batch: List[NDArray[(Any), np.float]], lr) -> Tuple[float, float]:
    if self.use_gpu:
        state_batch = Variable(torch.FloatTensor(state_batch).cuda())
        probs_batch = Variable(torch.FloatTensor(probs_batch).cuda())
        value_batch = Variable(torch.FloatTensor(value_batch).cuda())
    else:
        state_batch = Variable(torch.FloatTensor(state_batch))
        probs_batch = Variable(torch.FloatTensor(probs_batch))
        value_batch = Variable(torch.FloatTensor(value_batch))

    self.optimizer.zero_grad()
    for param_group in self.optimizer.param_groups:
        param_group['lr'] = lr

    log_act_probs, value = self.policy_value_net(state_batch)
    # loss = (z - v)^2 - pi*T * log(p) + c||theta||^2
    value_loss = F.mse_loss(value.view(-1), value_batch)
    policy_loss = -torch.mean(torch.sum(probs_batch * log_act_probs, 1))
    loss = value_loss + policy_loss
    loss.backward()
    self.optimizer.step()
    entropy = -torch.mean(torch.sum(torch.exp(log_act_probs) * log_act_probs, 1))
    return loss.item(), entropy.item()

参考资料

• Youtube, Deepmind AlphaZero - Mastering Games Without Human Knowledge, David Silver

• Mastering the game of Go with deep neural networks and tree search

• Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm

• AlphaGo Zero论文解析

• AlphaZero实战：从零学下五子棋（附代码）

AlphaGo Zero是Deepmind 最后一代AI围棋算法，因为已经达到了棋类游戏AI的终极目的：给定任何游戏规则，AI从零出发只通过自我对弈的方式提高，最终可以取得超越任何对手（包括顶级人类棋手和上一代AlphaGo）的能力。换种方式说，当给定足够多的时间和计算资源，可以取得无限逼近游戏真实解的能力。这一篇，我们深入分析AlphaGo Zero的设计理念和关键组件的细节并解释组件之间的关联。下一篇中，我们将在已有的N子棋OpenAI Gym 环境中用Pytorch实现一个简化版的AlphaGo Zero算法。

• 第一篇: Leetcode中的Minimax 和 Alpha Beta剪枝

• 第二篇: 井字棋Leetcode系列题解和Minimax最佳策略实现

• 第三篇: 井字棋、五子棋的OpenAI Gym GUI环境

• 第四篇: AlphaGo Zero 强化学习算法原理深度分析

• 第五篇: 井字棋、五子棋AlphaGo Zero 算法实战

AlphaGo Zero 综述

AlphaGo Zero 作为Deepmind在围棋领域的最后一代AI Agent，已经可以达到棋类游戏的终极目标：在只给定游戏规则的情况下，AI 棋手从最初始的随机状态开始，通过不断的自我对弈的强化学习来实现超越以往任何人类棋手和上一代Alpha的能力，并且同样的算法和模型应用到了其他棋类也得出相同的效果。这一篇，从原理上来解析AlphaGo Zero的运行方式。

AlphaGo Zero 算法由三种元素构成：强化学习（RL）、深度学习（DL）和蒙特卡洛树搜索（MCTS，Monte Carlo Tree Search）。核心思想是基于神经网络的Policy Iteration强化学习，即最终学的是一个深度学习的policy network，输入是某棋盘局面 s，输出是此局面下可走位的概率分布：\(p(a|s)\)。

在第一代AlphaGo算法中，这个初始policy network通过收集专业人类棋手的海量棋局训练得来，再采用传统RL 的Monte Carlo Tree Search Rollout 技术来强化现有的AI对于局面落子（Policy Network）的判断。Monte Carlo Tree Search Rollout 简单说来就是海量棋局模拟，AI Agent在通过现有的Policy Network策略完成一次从某局面节点到最终游戏胜负结束的对弈，这个完整的对弈叫做rollout，又称playout。完成一次rollout之后，通过局面树层层回溯到初始局面节点，并在回溯过程中同步修订所有经过的局面节点的统计指标，修正原先policy network对于落子导致输赢的判断。通过海量并发的棋局模拟来提升基准policy network，即在各种局面下提高好的落子的\(p(a_{win}|s)\)，降低坏的落子的\(p(a_{lose}|s)\)

基准policy network返回 p(s) 如下 \[ p(a|s) = \begin{align*} \left\lbrace \begin{array}{r@{}l} 0.1, & & a = (0,2) \\ 0.05, & & a = (1,0) \\ 0.5, & & a = (1,1) \\ 0.05, & & a = (1,2)\\ 0.2, & & a = (2,0) \\ 0.05, & & a = (2,1) \\ 0.05, & & a = (2,2) \end{array} \right. \end{align*} \] 通过海量并发模拟后，修订成如下的action概率分布，然后通过policy iteration迭代新的网络来逼近 \(p'\) 就提高了棋力。 \[ p'(a|s) = \begin{align*} \left\lbrace \begin{array}{r@{}l} 0, & & a = (0,2) \\ 0, & & a = (1,0) \\ 0.9, & & a = (1,1) \\ 0, & & a = (1,2)\\ 0, & & a = (2,0) \\ 0, & & a = (2,1) \\ 0.1, & & a = (2,2) \end{array} \right. \end{align*} \]

蒙特卡洛树搜索（MCTS）概述

Monte Carlo Tree Search 是Monte Carlo 在棋类游戏中的变种，棋类游戏的一大特点是可以用动作(move)联系的决策树来表示，树的节点数量取决于分支的数量和树的深度。MCTS的目的是在树节点非常多的情况下，通过实验模拟（rollout, playout）的方式来收集尽可能多的局面输赢情况，并基于这些统计信息，将搜索资源的重点均衡地放在未被探索的节点和值得探索的节点上，减少在大概率输的节点上的模拟资源投入。传统MCTS有四个过程：Selection, Expansion, Simulation 和Backpropagation。下图是Wikipedia 的例子：

• Selection：从根节点出发，根据现有统计的信息和selection规则，选择子节点递归向下做决定，后面我们会详细介绍AlphaGo的UCB规则。图中节点的数字，例如根节点11/21，分别代表赢的次数和总模拟次数。从根节点一路向下分别选择节点 7/10, 1/6直到叶子节点3/3，叶子节点表示它未被探索过。

• Expansion：由于3/3节点未被探索过，初始化其所有子节点为0/0，图中3/3只有一个子节点。后面我们会看到神经网络在初始化子节点的时候起到的指导作用，即所有子节点初始权重并非相同，而是由神经网络给出估计。

• Simulation：重复selection和expansion，根据游戏规则递归向下直至游戏结束。

• Backpropagation：游戏结束在终点节点产生游戏真实的价值，回溯向上调整所有父节点的统计状态。

权衡 Exploration 和 Exploitation

在不断扩张决策树并收集节点统计信息的同时，MCTS根据规则来权衡探索目的（采样不足）或利用目的来做决策，这个权衡规则叫做Upper Confidence Bound（UCB）。典型的UCB公式如下：w表示通过节点的赢的次数，n表示通过节点的总次数，N是父节点的访问次数，c是调节Exploration 和 Exploitation权重的超参。

\[ {\frac{w_i}{n_i}} + c \sqrt{\frac{\ln N_i}{n_i}} \]

假设某节点有两个子节点s1, s2，它们的统计指标为 s1: w/n = 3/4，s2: w/n = 6/8，由于两者输赢比率一样，因此根据公式，访问次数少的节点出于Exploration的目的胜出，MCTS最终决定从s局面走向s1。

从第一性原理来理解AlphaGo Zero

前一代的AlphaGo已经战胜了世界冠军，取得了空前的成就，AlphaGo Zero 的设计目标变得更加General，去除围棋相关的处理和知识，用统一的框架和算法来解决棋类问题。 1. 无人工先验数据

改进之前需要专家棋手对弈数据来冷启动初始棋力

2. 无特定游戏特征工程

   无需围棋特定技巧，只包含下棋规则，可以适用到所有棋类游戏

3. 单一神经网络

   统一Policy Network和Value Network，使用一个共享参数的双头神经网络

4. 简单树搜索

   去除传统MCTS的Rollout 方式，用神经网络来指导MCTS更有效产生搜索策略

搜索空间的两个优化原则

原则1: 通过Value Network减少搜索的深度

原则2: 通过Policy Network减少搜索的宽度

神经网络结构

AlphaGo Zero 使用一个单一的深度神经网络来完成policy 和value的预测。具体实现方式是将policy network和value network合并成一个共享参数 $ $ 的双头网络。其中z是真实游戏结局的效用，范围为[-1, 1] 。

\[ (p, v)=f_{\theta}(s) \] \[ p_{a}=\operatorname{Pr}(a \mid s) \] \[ v = \mathop{\mathbb{E}}[z|s] \]

Monte Carlo Tree Search (MCTS) 建立了棋局搜索树，节点的初始状态由神经网络输出的p和v值来估计，由此初始的动作策略和价值预判就会建立在高手的水平之上。模拟一局游戏之后向上回溯，会同步更新路径上节点的统计数值并生成更好的MCTS搜索策略 \(\vec{\pi}\)。进一步来看，MCTS和神经网络互相形成了正循环。神经网络指导了未知节点的MCTS初始搜索策略，产生自我对弈游戏结局后，通过减小 \(\vec{p}\) 和\(\vec{\pi}\)的 Loss ，最终又提高了神经网络对于局面的估计能力。神经网络value network的提升也是通过不断减小网络预测的结果和最终结果的差异来提升。 因此，具体神经网络的Loss函数由三部分组成，value network的损失，policy network的损失以及正则项。 \[ l=\sum_{t}\left(v_{\theta}\left(s_{t}\right)-z_{t}\right)^{2}-\vec{\pi}_{t} \cdot \log \left(\vec{p}_{\theta}\left(s_{t}\right)\right) + c {\lVert \theta \rVert}^2 \]

AlphaGo Zero MCTS 具体过程

AlphaGo Zero的MCTS和传统MCTS都有相似的四个过程，但AlphaGo Zero的MCTS步骤相对更复杂。 首先，除了W/N统计指标之外，AlphaGo Zero的MCTS保存了决策边 a|s 的Q(s,a)：Action Value，也就是Q-Learning中的Q值，其初始值由神经网络给出。此外，Q 值也用于串联自底向上更新节点的Value值。具体说来，当某个新节点被Explore后，会将网络给出的Q值向上传递，并逐层更新父节点的Q值。当游戏结局产生时，也会向上更新所有父节点的Q值。 此外对于某一游戏局面s进行多次模拟，每次在局面s出发向下探索，每次探索在已知节点按Selection规则深入一步，直至达到未探索的局面或者游戏结束，产生Q值后向上回溯到最初局面s，回溯过程中更新路径上的局面的统计值或者Q值。在多次模拟结束后根据Play的算法，决定局面s的下一步行动。尽管每次模拟探索可能会深入多层，但最终play阶段的算法规则仅决定给定局面s的下一层落子动作。多次向下探索的优势在于：

1. 探索和采样更多的叶子节点，在更多信息下做决策。

2. 通过average out多次模拟下一层落子决定，尽可能提升MCTS策略的下一步判断能力，提高 \(\pi\) 能力，更有效指导神经网络，提高其学习效率。

1. Selection:

从游戏局面s开始，选择a向下递归，直至未展开的节点（搜索树中的叶子节点）或者游戏结局。具体在局面s下选择a的规则由以下UCB(Upper Confidence Bound)决定
\[ a=\operatorname{argmax}_a(Q(s,a) + u(s,a)) \]

其中，Q(s,a) 和u(s,a) 项分别代表Exploitation 和Exploration。两项相加来均衡Exploitation和Exploration，保证初始时每个节点被explore，在有足够多的信息时逐渐偏向exploitation。

\[ u(s, a)=c_{p u c t} \cdot P(s, a) \cdot \frac{\sqrt{\Sigma_{b} N(s, b)}}{1+N(s, a)} \]

2. Expand

当遇到一个未展开的节点（搜索树中的叶子节点）时，对其每个子节点使用现有网络进行预估，即

\[ (p(s), v(s))=f_{\theta}(s) \]

3. Backup

当新的叶子节点展开时或者到达终点局面时，向上更新父节点的Q值，具体公式为 \[ Q(s, a)=\frac{1}{N(s, a)} \sum_{s^{\prime} \mid s, a \rightarrow s^{\prime}} V\left(s^{\prime}\right) \]

4. Play

多次模拟结束后，使用得到搜索概率分布 ${a} $来确定最终的落子动作。正比于访问次数的某次方 $ {a} N(s, a)^{1 / }\(，其中\)$为温度参数（temperature parameter）。

参考资料

• Youtube, Deepmind AlphaZero - Mastering Games Without Human Knowledge, David Silver

• Mastering the game of Go with deep neural networks and tree search

• Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm

• AlphaGo Zero论文解析

• AlphaZero实战：从零学下五子棋（附代码）