导读:极大似然估计(MLE) 是统计机器学习中最基本的概念,但是能真正全面深入地理解它的性质和背后和其他基本理论的关系不是件容易的事情。极大似然估计和以下概念都有着紧密的联系:随机变量,无偏性质(unbiasedness),一致估计(consistent),asymptotic normality,最优化(optimization),Fisher Information,MAP(最大后验估计),KL-Divergence,sufficient statistics等。在众多阐述 MLE 的文章或者课程中,总体来说都比较抽象,注重公式推导。本系列文章受3blue1brown 可视化教学的启发,坚持从第一性原理出发,通过数学原理结合模拟和动画,深入浅出地让读者理解极大似然估计。
相关链接
抛硬币问题
我们来思考这个老套问题,考虑手上有一枚硬币,旋转(抛)硬币得到正反面的概率固定(令正面概率为\(\theta^{\star}\))但未知,我们如何能通过实验推测出 \(\theta^{\star}\)

朴素的想法是,不断尝试抛硬币,随着次数 n 的增多,正面的比例会趋近于 \(\theta^{\star}\)
对应到数学形式上,令我们对于 \(\theta^{\star}\) 的估计为 \(\hat{\theta}_{n}\),则希望 \[ \hat{\theta}_n = {n_{head} \over n} \to \theta^{\star} \text{ as n } \to \infty \]
模拟试验代码
假设我们尝试了n次,每次的结果为 \(x_i\),\(x_i\)为1(正面) 或 0(反面)。比如试了三次的结果是 [1, 0, 1],则 \(x_1=1, x_2=0, x_3=1\)。一般,我们将观察到的数据写成向量形式
\[X=[x_1, x_2, x_3]^T=[1, 0, 1]^{T}\]
我们知道硬币的正反结果符合伯努利分布,也就是 \[ \begin{align*} P_{ber}(x;\theta) = \left\lbrace \begin{array}{r@{}l} \theta &\text{ if x=1} \\ 1-\theta &\text{ if x=0} \end{array} \right. \end{align*} \]
因为 x 只有0,1两种取值,因此上式也可以写成等价如下的不含条件分支的形式 \[ P_{ber} = \theta^x \cdot (1-\theta)^x \]
假设 \(\theta^{\star} = 0.7\),如果做 n=10 次试验,结果应该比较接近7个1,3个0。
下面我们来模拟一下 n=10,看看结果如何。
下面代码的实现上我们直接使用了pytorch 内置的 bernoulli 函数生成 n 个随机变量实例
1 | def gen_coins(theta, n=1): |
让我们来做三次 n=10 的试验
1 | for i in range(3): |
能发现 7个1,3个0 确实是比较可能的结果。
1 | trial 0 |
生成概率
直觉告诉我们,当 \(\theta^{\star}=0.7\) 时,根据 $P_{ber}(x;) $,7个1,3个0 出现的概率应该是最大,6个1,4个0 或者 8个1,2个0 这两种情况出现概率稍小,其他的情况概率更小。通过基本概率和伯努利公式,重复 n 次试验 1和0出现的概率可以由下面公式算出。(注:7个1,3个0不是单一事件,需要乘以组合数算出实际概率)
\[ P_{X} = \theta^{heads} \cdot (1-\theta)^{tails} \cdot {n \choose heads} \]
| P(X) | |
|---|---|
| head=0 | 0.000006 |
| head=1 | 0.000138 |
| head=2 | 0.000032 |
| head=3 | 0.001447 |
| head=4 | 0.036757 |
| head=5 | 0.102919 |
| head=6 | 0.200121 |
| head=7 | 0.266828 |
| head=8 | 0.233474 |
| head=9 | 0.121061 |
| head=10 | 0.028248 |
画出图看的很明显,1出现7次的概率确实最大。
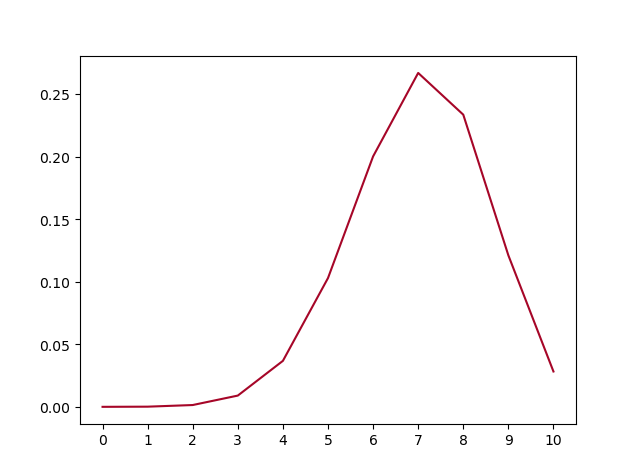
回到我们的问题,我们先假定 \(\theta^{\star} = 0.7\) 的硬币做 n=10 次试验的结果就是 7个1,3个0,或者具体序列为 [1, 0, 0, 1, 0, 1, 1, 1, 1, 1]。那么我们希望按照某种方法推测的估计值 \(\hat\theta\) 也为 0.7。
若将这个方法也记做 \(\hat\theta\),它是\(X\) 的函数,即 \(\hat\theta(X=[1, 0, 0, 1, 0, 1, 1, 1, 1, 1]^T)=0.7\)
我们如何构建这个方法呢?很显然,\(X\) 中 1 的个数就可以胜任,\(\hat\theta=\bar X\)。这个方式确实是正确的,后面的文章我们也会证明它是MLE在伯努利分布参数估计时的计算方法。
但是伯努利分布参数估计的问题中是最简单的情况,背后对应的更一般的问题是:假设我们知道某个过程或者实验生成了某种分布 P,但是不知道它的参数 \(\theta\),如何能通过反复的试验来推断 \(\theta\),同时,我们希望随着试验次数的增多,\(\hat\theta\) 能逼近 \(\theta\)。
由于过程是有随机性,试验结果 \(X\) 并不能确定一定是从 \(\hat\theta\) 生成的,因此我们需要对所有 \(\theta\) 打分。对于抛硬币试验来说,我们穷举所有在 [0, 1] 范围内的 \(\theta\),定义它的打分函数 \(f(\theta)\),并且希望我们定义的 \(f(\theta;X=[1, 0, 0, 1, 0, 1, 1, 1, 1, 1]^T)\) 在 \(\theta=0.7\) 时得分最高。推广到一般场景,有如下性质 \[ f(\theta^\star;X) >= f(\theta;X) \]
如此,我们将推测参数问题转换成了优化问题 \[ \hat\theta = \theta^{\star} = \operatorname{argmax}_{\theta} f(\theta; X) = 0.7 \]
朴素方法
一种朴素的想法是,由于 \(\theta^\star=0.7\),因此我们每次的结果应该稍微偏向 1,如果出现了 1,就记0.7分,出现了0,记0.3分,那么我们可以用10个结果的总分来定义总得分,即最大化函数
\[ \begin{equation*} \begin{aligned} &\operatorname{argmax}_{\theta} f(\theta) \\ =& \operatorname{argmax}_{\theta} P(x_1) + P(x_2) + ... + P(x_n) \\ =& \operatorname{argmax}_{\theta} P(x_1|\theta) + P(x_2|\theta) + ... + P(x_n|\theta) \\ =& \operatorname{argmax}_{\theta} \sum P(x_i|\theta) \\ \end{aligned} \end{equation*} \]
很可惜,我们定义的 f 并不符合 \(\theta=0.7\) 时取到最大的原则。下面画出了 \(\theta\) 在 [0, 1] 范围内 f 值,X 固定为 [1, 0, 0, 1, 0, 1, 1, 1, 1, 1]。显然,极值在 0.5 左右。
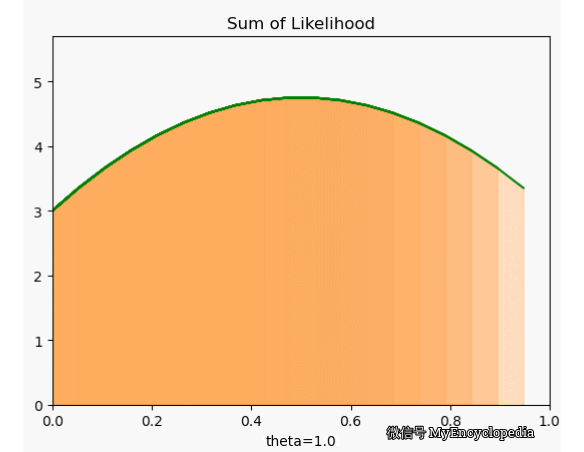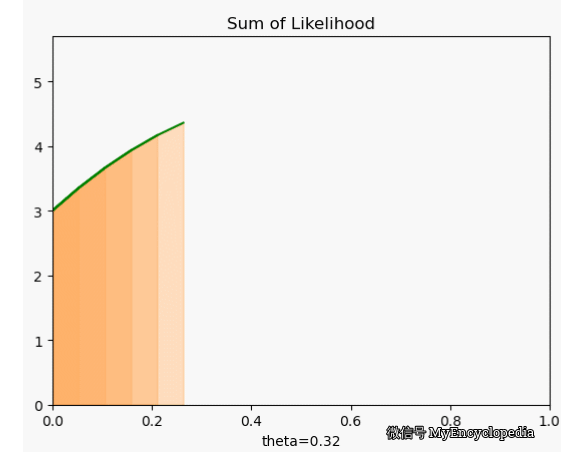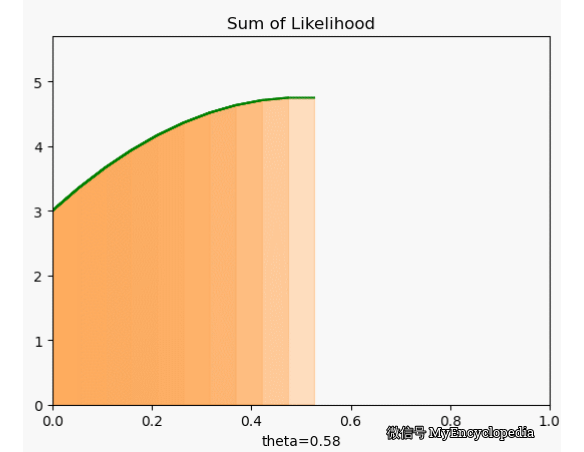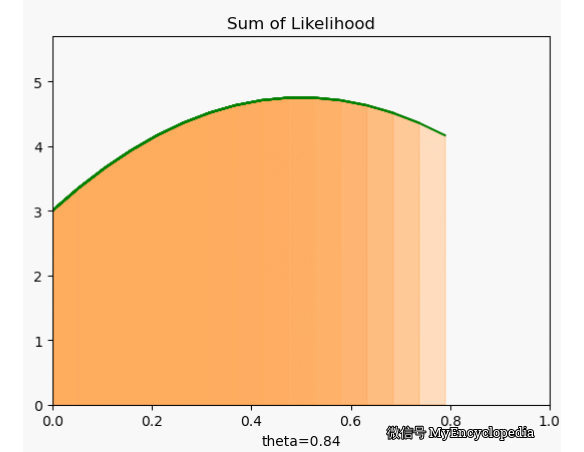
这种对于观察到的变量实例在整个参数空间打分的方法是最大似然方法的雏形。我们将每次试验结果对于不同 \(\theta\) 的打分就是似然函数的概念。
伯努利似然函数(Likelihood)
伯努利单个结果的似然函数 \(l(\theta)\) 视为 \(\theta\) 的函数,x视为给定值,它等价于概率质量函数 PMF
\[ l(\theta|x) = \theta^x \cdot (1-\theta)^x \]
极大似然估计(MLE)
有了单个结果的似然函数,我们如何定义 \(f(\theta)\) 呢?我们定义的 \(f(\theta)\) 需要满足,在 \(\theta^\star=0.7\) ,\(n=10\) 的情况下,试验最有可能的结果是 7 个1,3个0,此时 f 需要在 \(\theta=0.7\) 时取到最大值。
极大似然估计(MLE) 为我们定义了合理的 \(f(\theta)\) ,和朴素的想法类似,但是这次用单个结果的似然函数连乘而非连加 \[ L(\theta|X) = l(\theta|x_1) \cdot l(\theta|x_2) \cdot ...l(\theta|x_n) = \prod l(\theta|x_i) \]
我们再来看一下当 $X=[1, 0, 0, 1, 0, 1, 1, 1, 1, 1] $ 时 \(L\) 在 \(\theta\) 空间的取值情况,果然,MLE 能在 0.7时取到最大值。
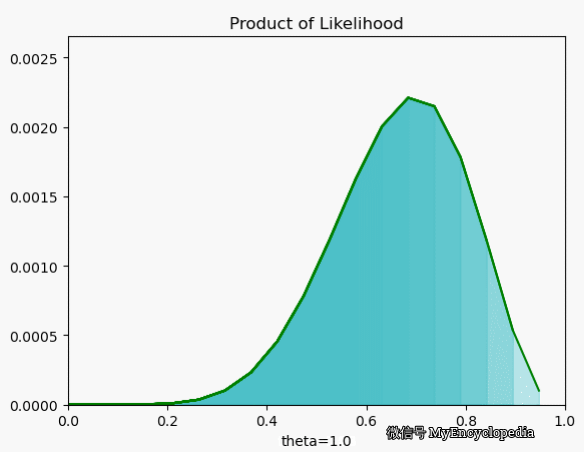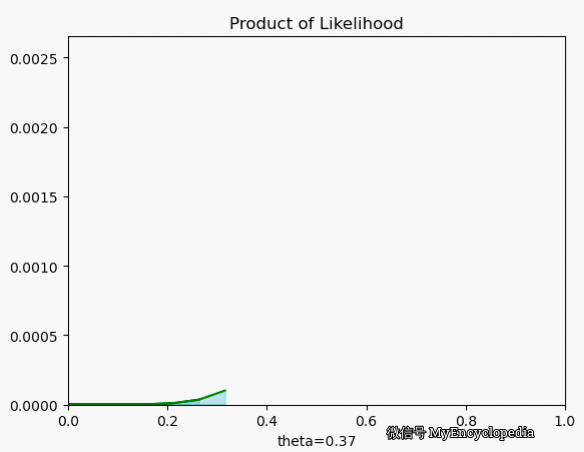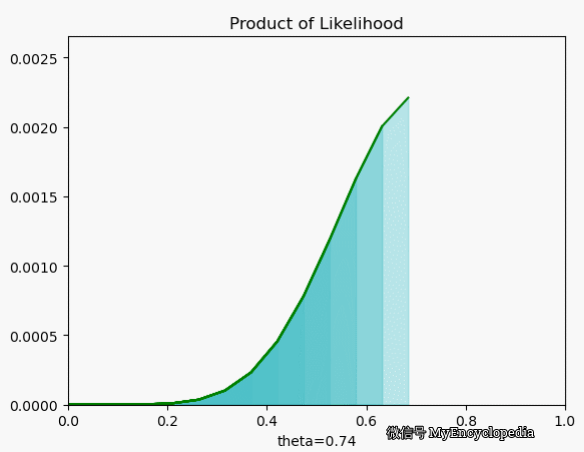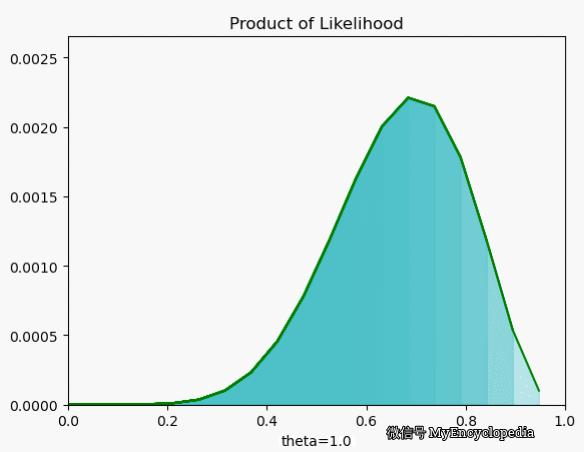
对数似然函数
最大似然函数 $_{} L() $ 能让我们找到最可能的 \(\theta\),但现实中,我们一般采用最大其 log 的形式。
\[ \begin{equation*} \begin{aligned} &\operatorname{argmax}_{\theta} \log L(\theta|X) \\ =& \operatorname{argmax}_{\theta} \log [l(\theta|x_1) \cdot l(\theta|x_2) \cdot ... \cdot l(\theta|x_n)] \\ =& \operatorname{argmax}_{\theta} \log l(\theta|x_1) + \log l(\theta|x_2) \cdot ... + \log l(\theta|x_n) \end{aligned} \end{equation*} \]
理论能证明,最大对数似然函数得到的极值等价于最大似然函数。但这么做有什么额外好处呢?
我们先将对数似然函数画出来
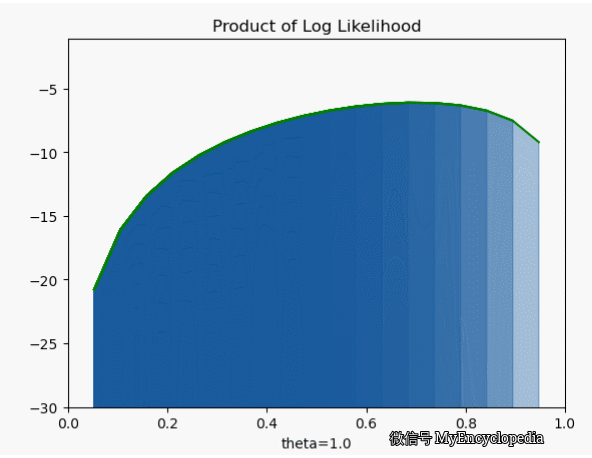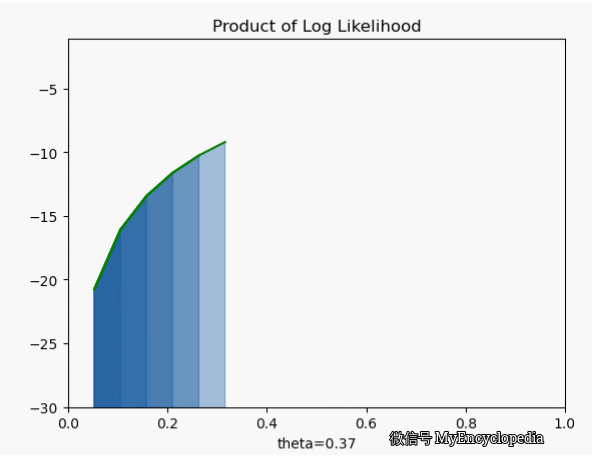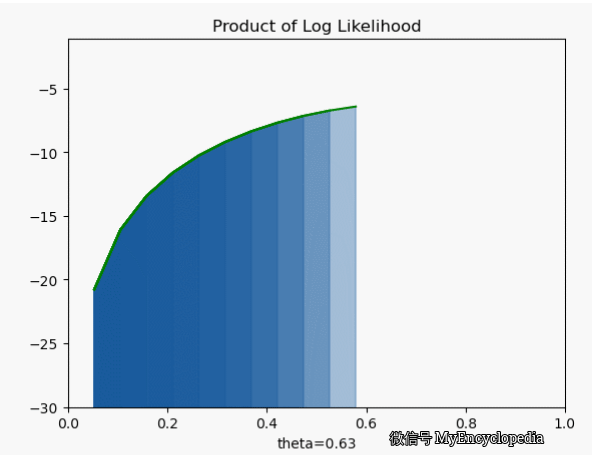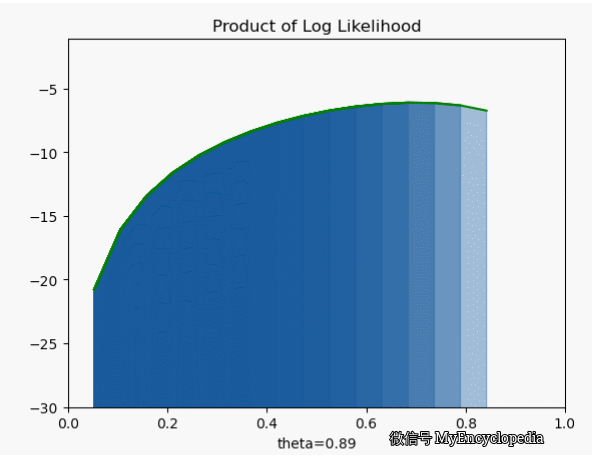
它的极大值也在 0.7,但是我们发现对数似然函数是个 concave 函数。在优化领域,最大化 concave 函数或者最小化 convex 函数可以有非常高效的解法。再仔细看之前的似然函数,它并不是一个 concave 函数。另一个非常重要的好处是,随着 n 的增大,连乘会导致浮点数 underflow,而单个点的对数似然函数的和的形式就不会有这个问题。
Pytorch MLE 代码
就让我们来实践一下,通过 pytorch 梯度上升来找到极值点。
1 | from stats.coin import gen_coins |
一点需要说明的是,在迭代过程中,我们保存最后三个导数的值,当最新的三个导数都很小时就退出迭代。
1 | if all(map(lambda x: abs(x) < 1, recent)) |
运行代码,能发现最大化对数似然函数能很稳定的找到 \(\theta\)。
现在大家对于伯努利MLE有了一定了解,接着,我们来思考一下最大化似然函数方法是否随着观察次数的增多能不断逼近真实的 \(\theta^\star\)呢?
MLE \(\theta\) 估计的收敛性
\(\theta^\star=0.7\) 的情况下,我们来这样做试验,第一次做 n=1生成观察数据 \(X_{1}\),第二次做 n=2生成观察数据 \(X_{2}\) \[ X_1,X_2, X_3, ..., X_N \] 对于每个数据集 \(X_i\) 通过最大似然方法求得估计的 \(\hat\theta\) \[ \hat\theta_1=MLE(X_1), \hat\theta_2=MLE(X_2), ..., \hat\theta_N=MLE(X_N) \] 将这些 \(\hat\theta_i\) 画出来,可以看到,随着 \(n \to \infty\),\(\hat\theta_i \to \theta^\star=0.7\)
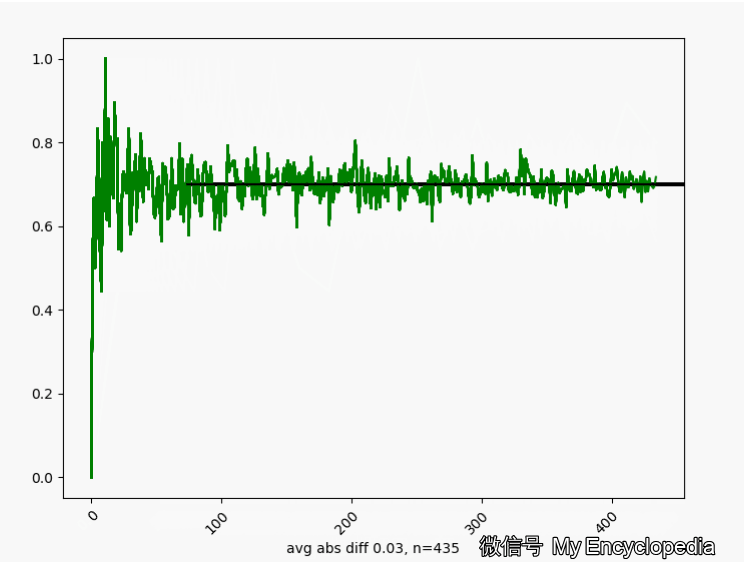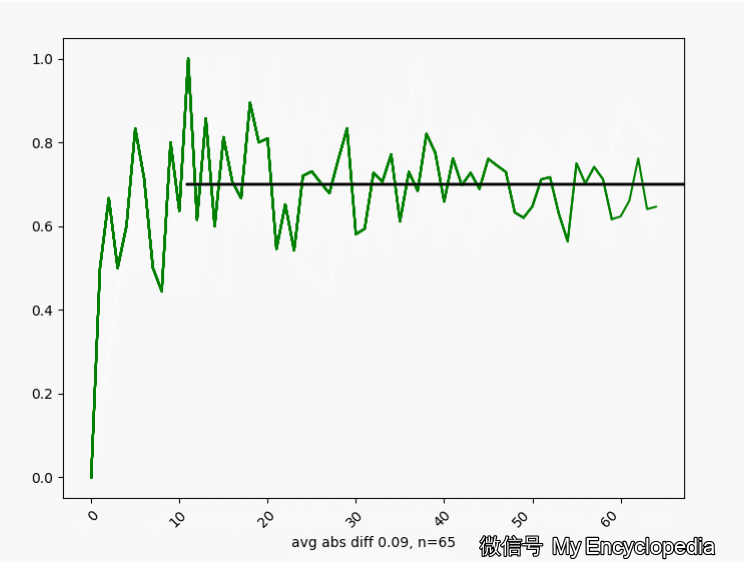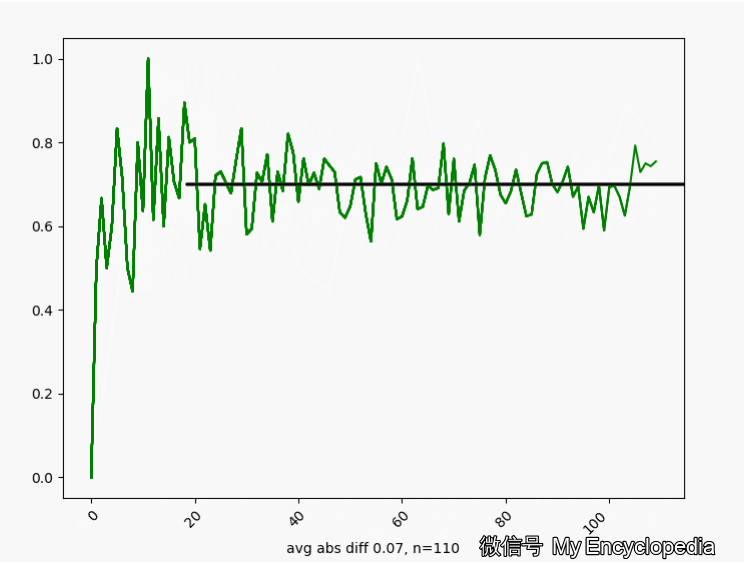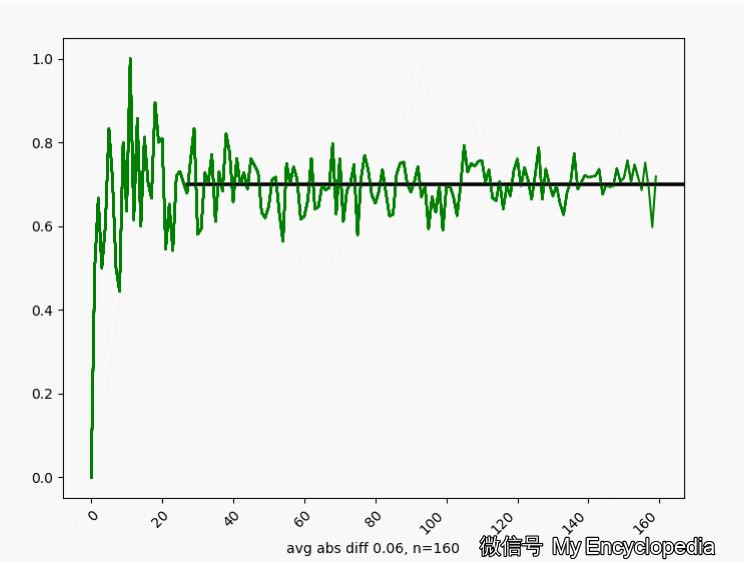
换一个角度来看一下,我们将 \(\hat\theta_i\) 数列按照顺序,离散化后再归一化比例,如下图画出来,红色的柱代表了最新的值 \(\hat\theta\)。可以发现,初始时候,\(\hat\theta\) 在较远离 0.7 的地方出现,随着 n 的增大,出现的位置比较接近 0.7。
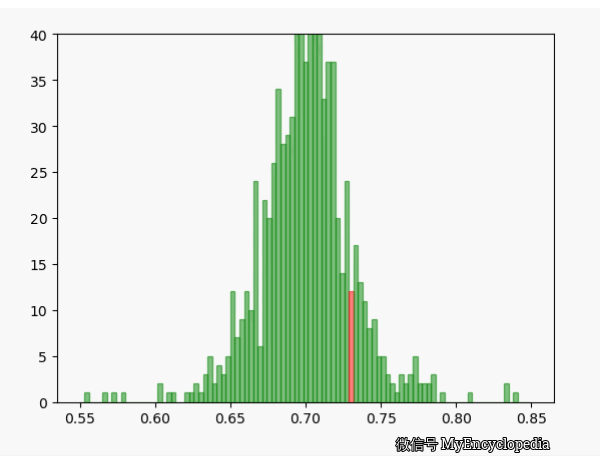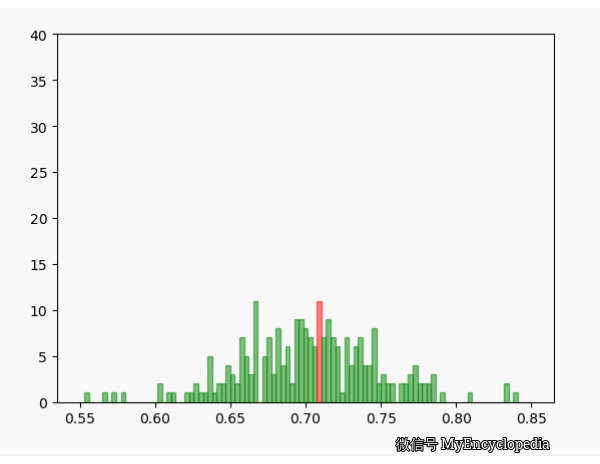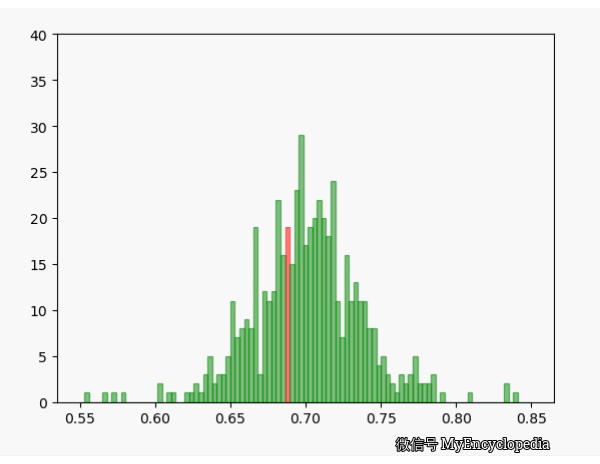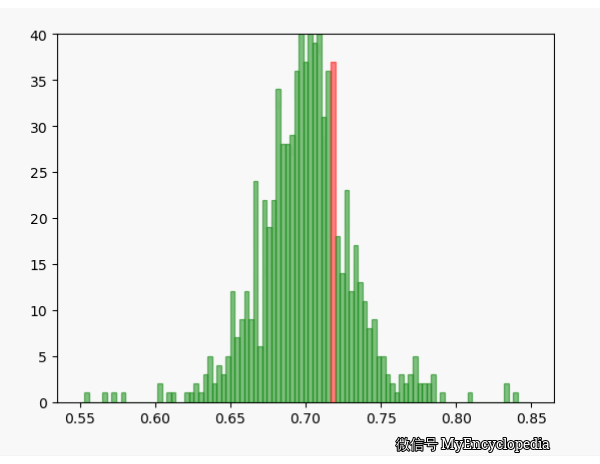
MLE \(\theta\) 估计的偏差和方差
我们已经知道 MLE 方法可以通过观察数据推测出最有可能的 \(\hat\theta\),由于观察数据 \(X\) 是伯努利过程产生的,具有随机性,那么 \(\hat\theta\) 可以看成是 \(\theta^\star\) 的随机变量。我们已经通过上面的试验知道随着试验次数的增大,我们的估计会越来越逼近真实值,现在的问题是对于固定的n,\(\hat\theta\) 的方差是多少,它的均值是否是无偏的呢?
带着这样的疑问,我们现在做如下试验:
固定 n=10,重复做实验,画出随着次数增多 \(\hat\theta\) 的分布,见图中绿色部分。同样的,红色是 n=80 不断试验的分布变换。
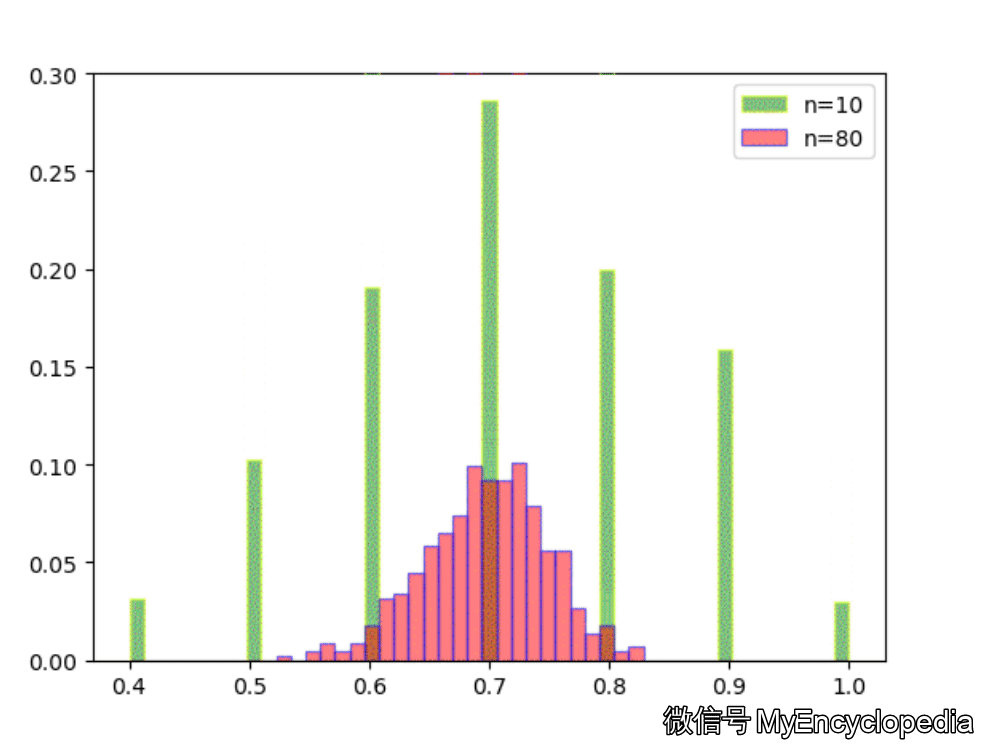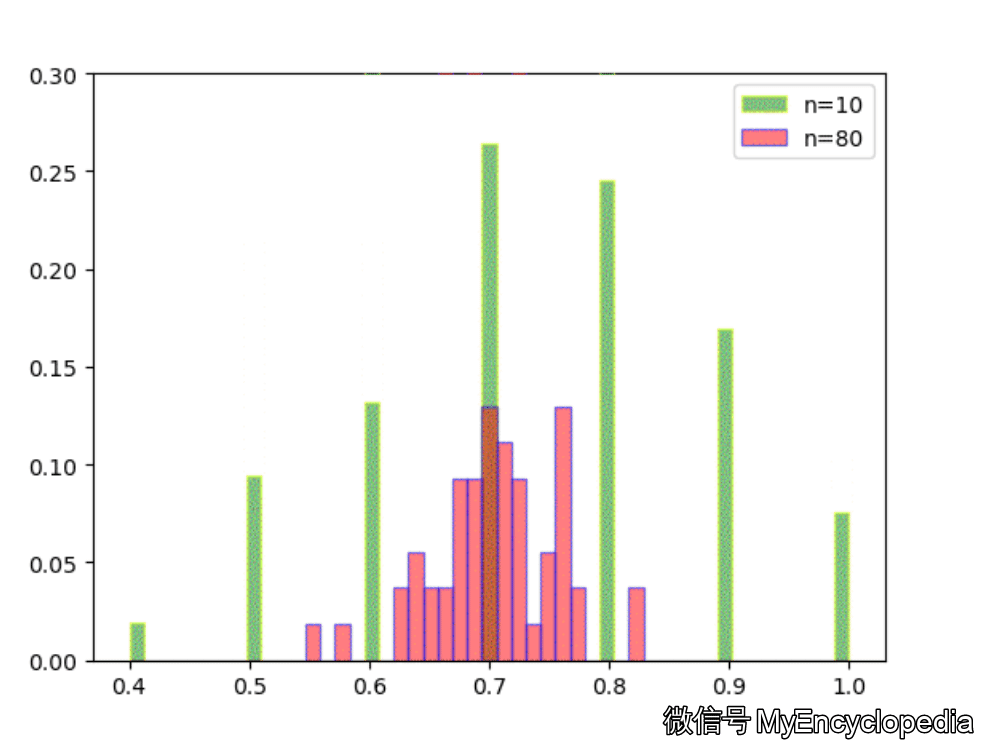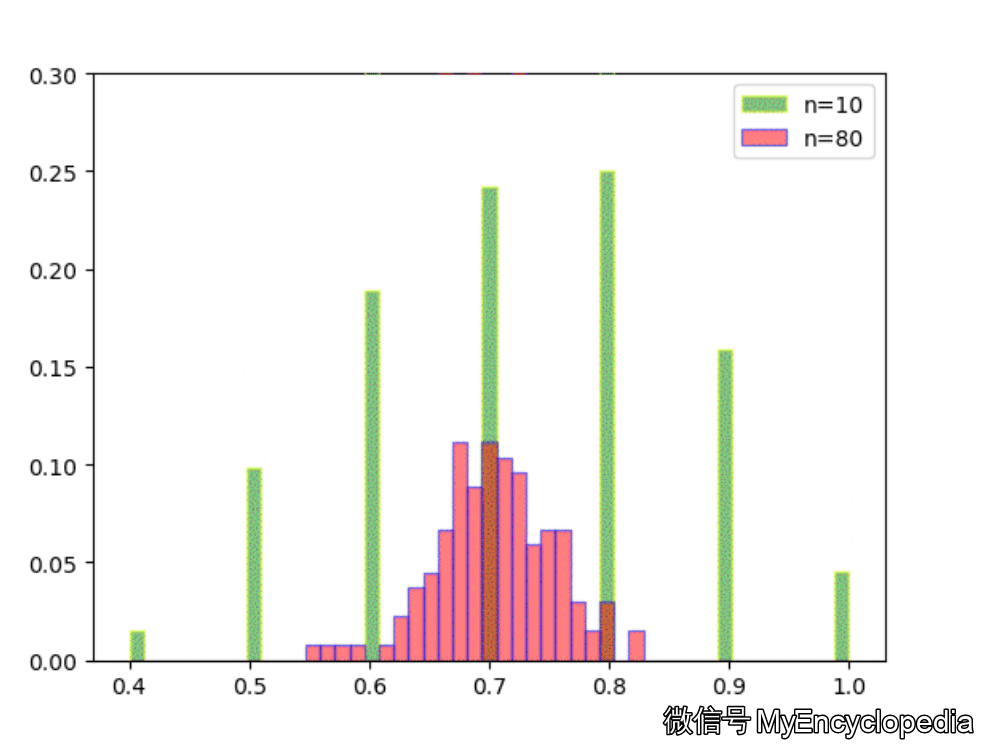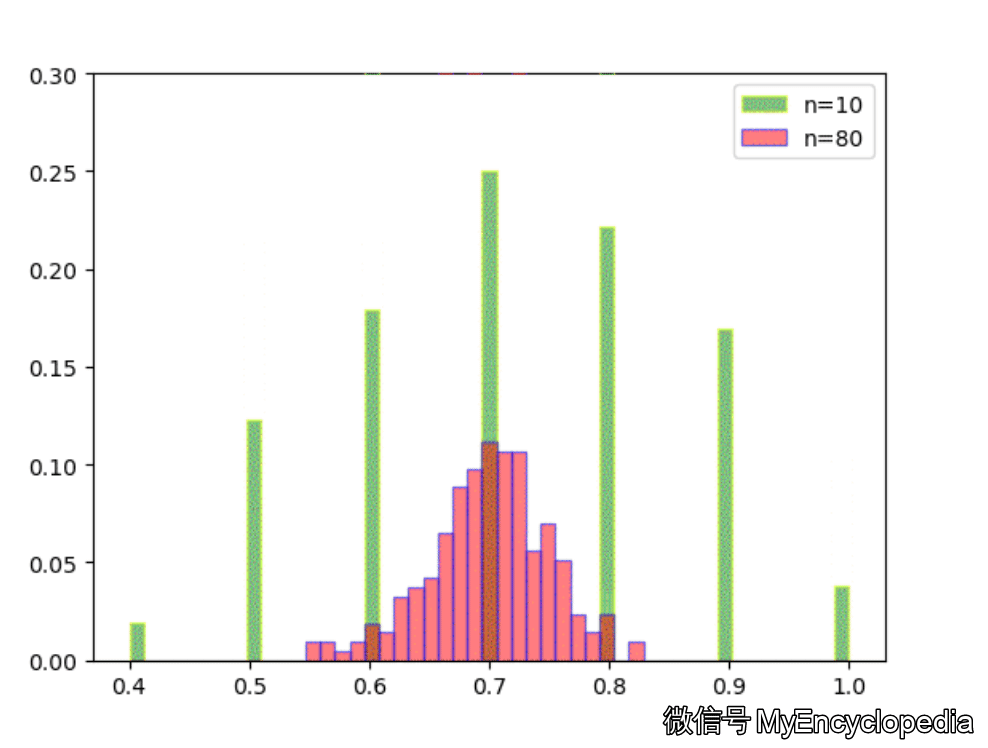
看的出来,随着试验次数的增多 - \(\hat\theta_{10}, \hat\theta_{80}\) 都趋近于正态分布
\(\hat\theta_{10}\) 的分散度比 $ _{80}$ 要大,即方差要大
\(\hat\theta_{10}, \hat\theta_{80}\) 的均值都在 0.7