这一期我们进入第六章:时序差分学习(Temporal-Difference Learning)。TD Learning本质上是加了bootstrapping的蒙特卡洛(MC),也是model-free的方法,但实践中往往比蒙特卡洛收敛更快。我们选取OpenAI Gym中经典的CartPole环境来讲解TD。更多相关内容,欢迎关注 本公众号 MyEncyclopedia。
CartPole OpenAI 环境
如图所示,小车上放了一根杆,杆会根据物理系统定理因重力而倒下,我们可以控制小车往左或者往右,目的是尽可能地让杆保持树立状态。

CartPole 观察到的状态是四维的float值,分别是车位置,车速度,杆角度和杆角速度。下表为四个维度的值范围。给到小车的动作,即action space,只有两种:0,表示往左推;1,表示往右推。
| Min | Max | |
|---|---|---|
| Cart Position | -4.8 | 4.8 |
| Cart Velocity | -Inf | Inf |
| Pole Angle | -0.418 rad (-24 deg) | 0.418 rad (24 deg) |
| Pole Angular Velocity | -Inf | Inf |
离散化连续状态
从上所知,CartPole step() 函数返回了4维ndarray,类型为float32的连续状态空间。对于传统的tabular方法来说第一步必须离散化状态,目的是可以作为Q table的主键来查找。下面定义的State类型是离散化后的具体类型,另外 Action 类型已经是0和1,不需要做离散化处理。
1 | State = Tuple[int, int, int, int] |
离散化处理时需要考虑的一个问题是如何设置每个维度的分桶策略。分桶策略会决定性地影响训练的效果。原则上必须将和action以及reward强相关的维度做细粒度分桶,弱相关或者无关的维度做粗粒度分桶。举个例子,小车位置本身并不能影响Agent采取的下一动作,当给定其他三维状态的前提下,因此我们对小车位置这一维度仅设置一个桶(bucket size=1)。而杆的角度和角速度是决定下一动作的关键因素,因此我们分别设置成6个和12个。
以下是离散化相关代码,四个维度的 buckets=(1, 2, 6, 12)。self.q是action value的查找表,具体类型是shape 为 (1, 2, 6, 12, 2) 的ndarray。
1 | class CartPoleAbstractAgent(metaclass=abc.ABCMeta): |
train() 方法串联起来 agent 和 env 交互的流程,包括从 env 得到连续状态转换成离散状态,更新 Agent 的 Q table 甚至 Agent的执行policy,choose_action会根据执行 policy 选取action。
1 | def train(self, num_episodes=2000): |
choose_action 的默认实现为基于现有 Q table 的 \(\epsilon\)-greedy 策略。
1 | def choose_action(self, state) -> Action: |
抽象出公共的基类代码 CartPoleAbstractAgent 之后,SARSA、Q-Learning和Expected SARSA只需要复写 update_q 抽象方法即可。
1 | class CartPoleAbstractAgent(metaclass=abc.ABCMeta): |
TD Learning的精髓
在上一期,本公众号 MyEncyclopedia 的21点游戏的蒙特卡洛On-Policy控制介绍了Monte Carlo方法,知道MC需要在环境中模拟直至最终结局。若记\(G_t\)为t步以后的最终return,则 MC online update 版本更新为:
\[ V(S_t) \leftarrow V(S_t) + \alpha[G_{t} - V(S_t)] \]
可以认为 \(V(S_t)\) 向着目标为 \(G_t\) 更新了一小步。
而TD方法可以只模拟下一步,得到 \(R_{t+1}\),而余下步骤的return,\(G_t - R_{t+1}\) 用已有的 \(V(S_{t+1})\) 来估计,或者统计上称作bootstrapping。这样 TD 的更新目标值变成 \(R_{t+1} + \gamma V(S_{t+1})\),整体online update 公式则为: \[ V(S_t) \leftarrow V(S_t) + \alpha[R_{t+1} + \gamma V(S_{t+1})- V(S_t)] \]
概念上,如果只使用下一步 \(R_{t+1}\) 值然后bootstrap称为 TD(0),用于区分使用多步后的reward的TD方法。另外,变化的数值 \(R_{t+1} + \gamma V(S_{t+1})- V(S_t)\) 称为TD error。
另外一个和Monte Carlo的区别在于一般TD方法保存更精细的Q值,\(Q(S_t, A_t)\),并用Q值来boostrap,而MC一般用V值也可用Q值。
SARSA: On-policy TD 控制
SARSA的命名源于一次迭代产生了五元组 \(S_t,A_t,R_{t+1},S_{t+1},A_{t+1}\)。SARSA利用五个值做 action-value的 online update:
\[ Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[R_{t+1}+\gamma Q(S_{t+1}, A_{t+1}) - Q(S_t,A_t)] \]
对应的Q table更新实现为:
1 | class SarsaAgent(CartPoleAbstractAgent): |
SARSA 在执行policy 后的Q值更新是对于针对于同一个policy的,完成了一次策略迭代(policy iteration),这个特点区分于后面的Q-learning算法,这也是SARSA 被称为 On-policy 的原因。下面是完整算法伪代码。
\[ \begin{align*} &\textbf{Sarsa (on-policy TD Control) for estimating } Q \approx q_{*} \\ & \text{Algorithm parameters: step size }\alpha \in ({0,1}]\text{, small }\epsilon > 0 \\ & \text{Initialize }Q(s,a), \text{for all } s \in \mathcal{S}^{+}, a \in \mathcal{A}(s) \text{, arbitrarily except that } Q(terminal, \cdot) = 0 \\ & \text{Loop for each episode:}\\ & \quad \text{Initialize }S\\ & \quad \text{Choose } A \text{ from } S \text{ using policy derived from } Q \text{ (e.g., } \epsilon\text{-greedy)} \\ & \quad \text{Loop for each step of episode:} \\ & \quad \quad \text{Take action }A, \text { observe } R, S^{\prime} \\ & \quad \quad \text{Choose }A^{\prime} \text { from } S^{\prime} \text{ using policy derived from } Q \text{ (e.g., } \epsilon\text{-greedy)} \\ & \quad \quad Q(S,A) \leftarrow Q(S,A) + \alpha[R+\gamma Q(S^{\prime}, A^{\prime}) - Q(S,A)] \\ & \quad \quad S \leftarrow S^{\prime}; A \leftarrow A^{\prime} \\ & \quad \text{until }S\text{ is terminal} \\ \end{align*} \]
SARSA 训练分析
SARSA收敛较慢,1000次episode后还无法持久稳定,后面的Q-learning 和 Expected Sarsa 都可以在1000次episode学习长时间保持不倒的状态。
Q-Learning: Off-policy TD 控制
Q-Learning 是深度学习时代前强化学习领域中的著名算法,它的 online update 公式为: \[ Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[R_{t+1}+\gamma \max_{a}Q(S_{t+1}, a) - Q(S_t,A_t)] \]
对应的 update_q() 方法具体实现
1 | class QLearningAgent(CartPoleAbstractAgent): |
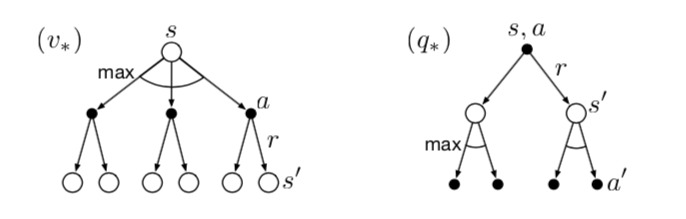
\[ \begin{aligned} q_{*}(s, a) &=\mathbb{E}\left[R_{t+1}+\gamma \max _{a^{\prime}} q_{*}\left(S_{t+1}, a^{\prime}\right) \mid S_{t}=s, A_{t}=a\right] \\ &=\mathbb{E}[R \mid S_{t}=s, A_{t}=a] + \gamma\sum_{s^{\prime}} p\left(s^{\prime}\mid s, a\right)\max _{a^{\prime}} q_{*}\left(s^{\prime}, a^{\prime}\right) \\ &\approx r + \gamma \max _{a^{\prime}} q_{*}\left(s^{\prime}, a^{\prime}\right) \end{aligned} \]
Q-Learning 被称为 off-policy 的原因是它并没有完成一次policy iteration,而是直接用已有的 Q 来不断近似 \(Q_{*}\)。
对比下面的Q-Learning 伪代码和之前的 SARSA 版本可以发现,Q-Learning少了一次模拟后的 \(A_{t+1}\),这也是Q-Learning 中执行policy和预估Q值(即off-policy)分离的一个特征。
\[ \begin{align*} &\textbf{Q-learning (off-policy TD Control) for estimating } \pi \approx \pi_{*} \\ & \text{Algorithm parameters: step size }\alpha \in ({0,1}]\text{, small }\epsilon > 0 \\ & \text{Initialize }Q(s,a), \text{for all } s \in \mathcal{S}^{+}, a \in \mathcal{A}(s) \text{, arbitrarily except that } Q(terminal, \cdot) = 0 \\ & \text{Loop for each episode:}\\ & \quad \text{Initialize }S\\ & \quad \text{Loop for each step of episode:} \\ & \quad \quad \text{Choose } A \text{ from } S \text{ using policy derived from } Q \text{ (e.g., } \epsilon\text{-greedy)} \\ & \quad \quad \text{Take action }A, \text { observe } R, S^{\prime} \\ & \quad \quad Q(S,A) \leftarrow Q(S,A) + \alpha[R+\gamma \max_{a}Q(S^{\prime}, a) - Q(S,A)] \\ & \quad \quad S \leftarrow S^{\prime}\\ & \quad \text{until }S\text{ is terminal} \\ \end{align*} \]
Q-Learning 训练分析
Q-Learning 1000次episode就可以持久稳定住。
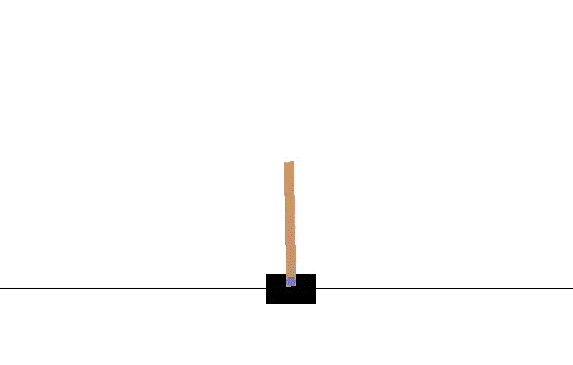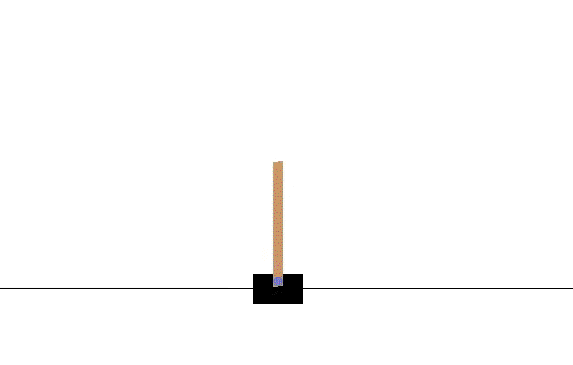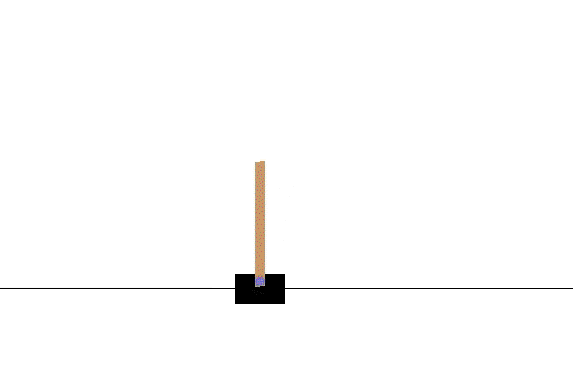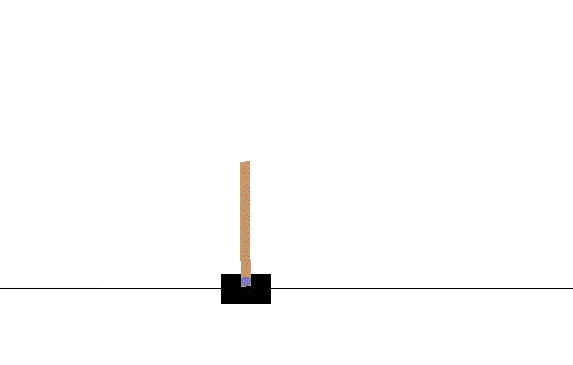
SARSA 改进版 Expected SARSA
Expected SARSA 改进了 SARSA 的地方在于考虑到了在某一状态下的现有策略动作分布,以此来减少variance,加快收敛,具体更新规则为:
\[ \begin{aligned} Q(S_t,A_t) &\leftarrow Q(S_t,A_t) + \alpha[R_{t+1}+\gamma \mathbb{E}_{\pi}[Q(S_{t+1}, A_{t+1} \mid S_{t+1})] - Q(S_t,A_t)] \\ &\leftarrow Q(S_t,A_t) + \alpha[R_{t+1}+\gamma \sum_{a} \pi\left(a\mid S_{t+1}\right) Q(S_{t+1}, a) - Q(S_t,A_t)] \\ \end{aligned} \]
注意在实现中,update_q() 不仅更新了Q table,还显示更新了执行policy \(\pi\)。
1 | class ExpectedSarsaAgent(CartPoleAbstractAgent): |
同样的,Expected SARSA 1000次迭代也能比较好的学到最佳policy。