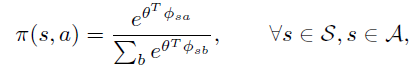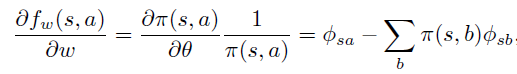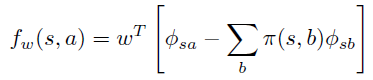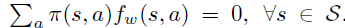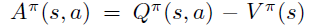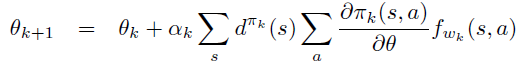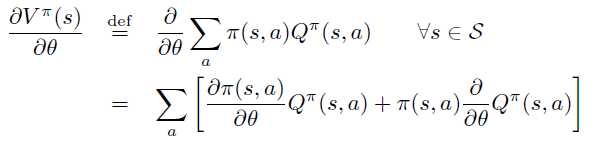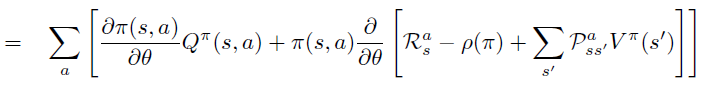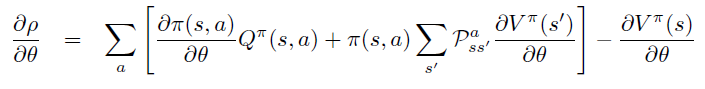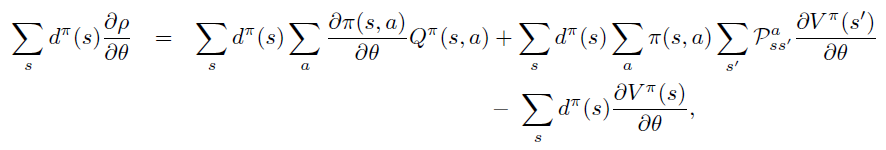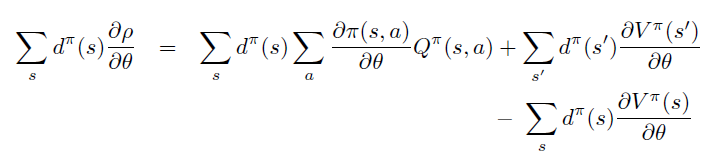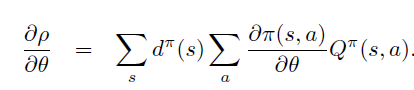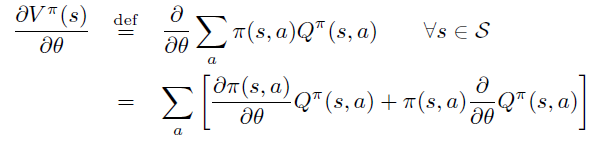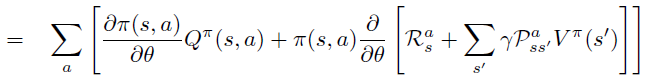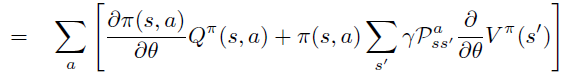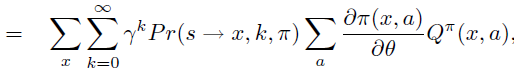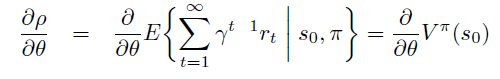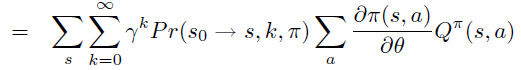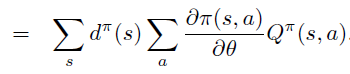导读:本论文由Berkeley 的几位大神于2015年发表于 JMLR(Journal of Machine Learning Research)。深度强化学习算法例如DQN或者PG(Policy Gradient)都无法避免训练不稳定的问题:在训练过程中效果容易退化并且很难恢复。针对这个通病,TRPO采用了传统优化算法中的trust region方法,以保证每一步迭代能够获得效果提升,直至收敛到局部最优点。
本篇论文涉及到的知识点比较多,不仅建立在强化学习领域经典论文的结论:Kakade & Langford 于2002 年发表的 Approximately Optimal Approximate Reinforcement Learning 关于优化目标的近似目标和重要性采样,也涉及到传统优化方法 trust region 的建模和其具体的矩阵近似数值算法。读懂本论文,对于深度强化学习及其优化方法可以有比较深入的理解。本论文附录的证明部分由于更为深奥和冗长,在本文中不做具体讲解,但是也建议大家能够仔细研读。
阅读本论文需要注意的是,这里解读的版本是arxiv的版本,这个版本带有附录,不同于 JMLR的版本的是,arxiv版本中用reward函数而后者用cost函数,优化方向相反。
arxiv 下载链接为 https://arxiv.org/pdf/1502.05477.pdf
0. 论文框架
本论文解决的目标是希望每次迭代参数能保证提升效果,具体想法是利用优化领域的 trust region方法(中文可以翻译成置信域方法或信赖域方法),通过参数在trust region范围中去找到一定能提升的下一次迭代。
本论文框架如下
首先,引入Kakade & Langford 论文 Approximately Optimal Approximate Reinforcement Learning 中关于近似优化目标的结论。(论文第二部分)
基于 Kakade 论文中使用mixture policy保证每一步效果提升的方法,扩展到一般随机策略,引入策略分布的total variation divergence作为约束。(论文第三部分)
将total variation divergence约束替换成平均 KL divergence 约束,便于使用蒙特卡洛方法通过采样来生成每一步的具体优化问题。(论文第四,五部分)
给出解决优化问题的具体算法,将优化目标用first order来近似,约束项用second order 来近似,由于second order涉及到构造Hessian matrix,计算量巨大,论文给出了 conjugate gradient + Fisher information matrix的近似快速实现方案。(论文第六部分)
从理论角度指出,Kakade 在2002年提出的方法natrual policy gradient 和经典的policy gradient 都是TRPO的特别形式。(论文第七部分)
评价TRPO在两种强化学习模式下的最终效果,一种是MuJoCo模拟器中能得到真实状态的模式,一种是Atari游戏环境,即观察到的屏幕像素可以信息完全地表达潜在真实状态的模式。(论文第八部分)
本文下面的小结序号和论文小结序号相同,便于对照查阅。
1. 介绍
TRPO 第一次证明了最小化某种 surrogate 目标函数且采用non-trivial的步长,一定可以保证策略提升。进一步将此 surrogate 目标函数转换成trust region约束下的优化问题。TRPO是一种on-policy 的算法,因为每一步迭代,需要在新的策略下通过采样数据来构建具体优化问题。
2. 已有理论基础
第二部分主要回顾了 Kakade & Langford 于2002 年的论文 Approximately Optimal Approximate Reinforcement Learning 中的一系列结论。
先来定义几个重要概念的数学定义
\(\eta(\pi)\) 是策略 \(\pi\) 的目标,即discounted reward 和的期望。
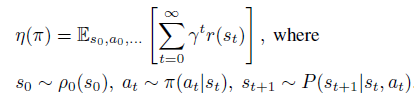
- 然后是策略的Q值和V值
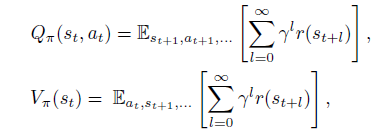
- 最后是策略的advantage函数
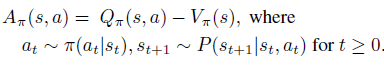
接着,开始引入 Kakade & Langford 论文结论,即下式(公式1)。
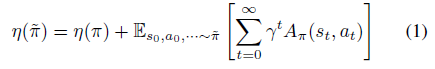
公式1表明,下一次迭代策略的目标可以分解成现有策略的目标 \(\eta(\pi)\) 和现有advantage 函数在新策略trajectory分布下的期望。
公式1可以很容易从trajectory分布转换成新策略在状态的访问频率,即公式2
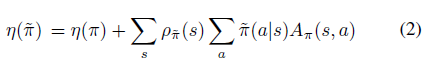
状态的访问频率或稳定状态分布定义成
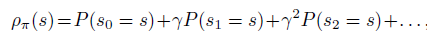
注意到公式2中状态的期望依然依赖于新策略 \(\rho_{\widetilde\pi}\) 的稳定状态分布,不方便实现。原因如下,期望形式有利于采样来解决问题,但是由于采样数据源于 on-policy \(\pi\) 而非 \({\widetilde\pi}\) ,因此无法直接采样未知的策略 \({\widetilde\pi}\)。
幸好,Kakade 论文中证明了,可以用 \(\rho_{\pi}\) 的代替 \(\rho_{\widetilde\pi}\) 并且证明了这种代替下的近似目标函数 \(L_{\pi}\) 是原来函数的一阶近似
\[ L_{\pi}(\widetilde\pi) \approx \eta(\widetilde\pi) \]
即满足
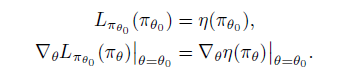
\(L_{\pi}\) 具体定义表达式为
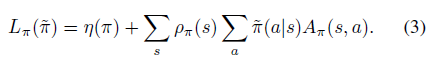
\(L_{\pi}(\widetilde\pi)\) 是一阶近似意味着在小范围区域中一定是可以得到提升的,但是范围是多大,是否能保证 \(\eta\) 的提升?Kakade的论文中不仅给出了通过mix新老策略的提升方式,还给出了这个方式对原目标 \(\eta\) 较 \(L_{\pi}(\widetilde\pi)\) 的提升下届。
策略更新规则如下
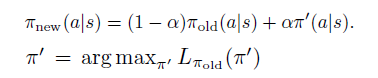
公式6为具体提升下届为
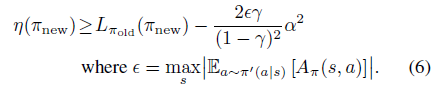
3. 扩展到随机策略
论文的这一部分将Kakade的mix policy update 扩展到一般的随机策略,同时依然保证每次迭代能得到目标提升。
首先,每次策略迭代必须不能和现有策略变化太大,因此,引入分布间常见的TV divergence,即 total variation divergence。
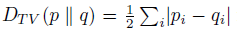
有了两个分布距离的定义,就可以定义两个策略的距离。离散状态下,一个策略是状态到动作分布的 map 或者 dict,因此,可以定义两个策略的距离为所有状态中最大的动作分布的 \(D_{TV}\),即
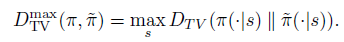
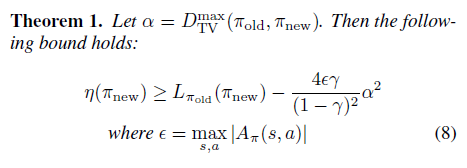
进一步将 TV divergence 转换成 KL divergence,转换成KL divergence 的目的是为了后续使用传统且成熟的 trust region 蒙特卡洛方法和 conjugate gradient 的优化近似解法。
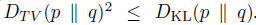
由于上面两种距离的大小关系,可以推导出用KL divergence表示的 \(\eta\) 较 \(L_{\pi}(\widetilde\pi)\) 的提升下届
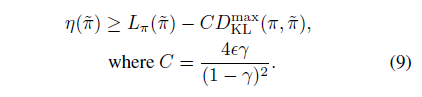
根据公式9,就可以形成初步的概念上的算法一,通过每一步形成无约束优化问题,同时保证每次迭代的 \(\pi_i\) 对应的 \(\eta\) 是递增的。

4. Trust Region Policy Optimization
看到这里已经不容易了,尽管算法一给出了一个解决方案,但是本论文的主角TRPO 还未登场。TRPO算法的作用依然是近似!
算法一对于下面的目标函数做优化,即每次找到下一个 \(\theta_i\) 最大化下式,\(\eta\) 每一步一定能得到提升。
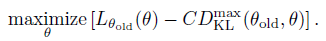
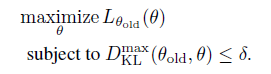
将 \(D^{max}_{KL}\) 放入约束项中符合trust region 这种传统优化解法。
关于 \(D^{max}_{KL}\) 约束,再补充两点
其定义是两个策略中所有状态中最大的动作分布的 \(D_{TV}\) ,因此它约束了所有状态下新老策略动作分布的KL散度,也就意味着有和状态数目相同数量的约束项,海量的约束项导致算法很难应用到实际中。
约束项的 trust region 不是参数 \(\theta\) 的空间,而是其KL散度的空间。
基于第一点,再次使用近似法,在约束项中用KL期望来代替各个状态下的KL散度,权重为on-policy 策略的分布 \(\rho(\theta_{old})\)
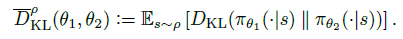
最终,得到TRPO在实际中的优化目标(12式):
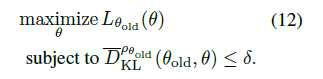
5. 用采样方法来Trust Region约束优化
论文第五部分,将TRPO优化目标12式改写成期望形式,引入两种蒙特卡洛方法 single path 和 vine 来采样。
具体来说,\(L_{\theta_{old}}\) 由两项组成 \[ L_{\theta_{old}} = \eta(\theta_{old}) + \sum_s \rho_{\theta_{old}}(s)\sum_a {\pi_{\theta}}(a |s) A_{\theta_{old}}(s,a) \]
第一项是常量,只需优化第二项,即优化问题等价为13式
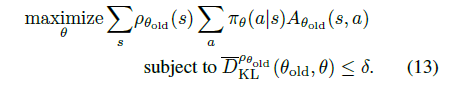
随后,为了可以适用非 on-policy \(\pi_{\theta_{old}}\) 的动作分布来任意采样,引入采样的动作分布 \(q(a|s)\),将13式中的 \(\sum_a\) 部分通过重要性采样改成以下形式:
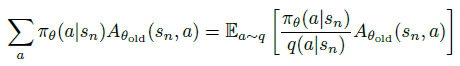
再将13式中的 \(\sum_s \rho(s)\) 改成期望形式 \(\mathbb{E}_{s \sim \rho}\) ,并将 \(A\) 改成 \(Q\) 值,得14式。
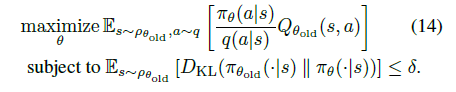
至此,我们得到trust region优化的期望形式:优化目标中期望的状态空间是基于 on-policy \(\pi_{\theta_{old}}\),动作空间是基于任意采样分布 \(q(a|s)\),优化约束中的期望是基于 on-policy \(\pi_{\theta_{old}}\)。
5.1 Single path采样
根据14式,single path 是最基本的的蒙特卡洛采样方法,和REINFORCE算法一样, 通过on-policy \(\pi_{\theta_{old}}\)生成采样的 trajectory数据: \(s_0, a_0, s_1, a_1, ..., a_{T-1}, s_{T}\),然后代入14式。注意,此时 \(q(a|s) = \pi_{\theta_{old}}(a|s)\),即用现有策略的动作分布直接代替采样分布。
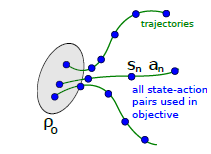
5.2 Vine 采样
虽然single path方法简单明了,但是有着online monte carlo方法固有的缺陷,即variance较大。Vine方法通过在一个状态多次采样来改善此缺陷。Vine的翻译是藤,寓意从一个状态多次出发来采样,如下图,\(s_n\) 状态下采样多个rollouts,很像植物的藤长出多分叉。当然,vine方法要求环境能restart 到某一状态,比如游戏环境通过save load返回先前的状态。
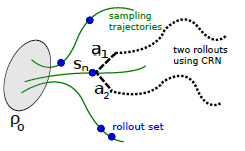
具体来说,vine 方法首先通过生成多个on-policy 的trajectories来确定一个状态集合 \(s_1, s_2, ..., s_N\)。对于状态集合的每一个状态 \(s_n\) 采样K个动作,服从 $ a_{n, k} q(s_{n}) $ 。接着,对于每一个 \((s_n, a_{n,k})\) 再去生成一次 rollout 来估计 \(\hat{Q}_{\theta_{i}}\left(s_{n}, a_{n, k}\right)\) 。试验证明,在连续动作空间问题中,\(q\left(\cdot \mid s_{n}\right)\) 直接使用 on-policy 可以取得不错效果,在离散空间问题中,使用uniform分布效果更好。
6. 转换成具体优化问题
再回顾一下现在的进度,12式定义了优化目标,约束项是KL divergence空间的trust region 形式。14式改写成了等价的期望形式,通过两种蒙特卡洛方法生成 state-action 数据集,可以代入14式得到每一步的具体数值的优化问题。论文这一部分简单叙述了如何高效但近似的解此类问题,详细的一些步骤在附录中阐述。我们把相关解读都放在下一节。
7. 和已有理论的联系
7.1 简化成 Natural Policy Gradient
再回到12式,即约束项是KL divergence空间的trust region 形式
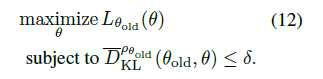
对于这种形式的优化问题,一般的做法是通过对优化目标做一阶函数近似,即 \[ L_{\theta_{old}}(\theta) \approx L_{\theta_{old}}\left(\theta_{old}\right)+g^{T}\left(\theta-\theta_{old}\right) \]
\[ \left.g \doteq \nabla_{\theta} L_{\theta_{old}}(\theta)\right|_{\theta_{old}} \]
并对约束函数做二阶函数近似,因为约束函数在 \(\theta_{old}\) 点取到极值,因此一阶导为0。 \[ \bar{D}_{K L}\left(\theta \| \theta_{old}\right) \approx \frac{1}{2}\left(\theta-\theta_{old}\right)^{T} H\left(\theta-\theta_{old}\right) \]
\[ \left.H \doteq \nabla_{\theta}^{2} \bar{D}_{K L}\left(\theta \| \theta_{old}\right)\right|_{\theta_{old}} \]
12式的优化目标可以转换成17式
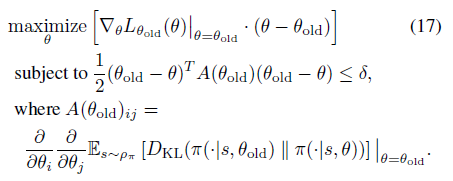
对应参数迭代更新公式如下
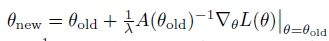
这个方法便是Kakade在2002年发表的 natrual policy gradient 论文。
7.2 简化成 Policy Gradient
注意,\(L_{\theta_{old}}\)的一阶近似的梯度 \[ \left.\nabla_{\theta} L_{\theta_{\text {old }}}(\theta)\right|_{\theta=\theta_{\text {old }}} \cdot\left(\theta-\theta_{\text {old }}\right) \]
即PG定理 \[ \frac{\partial \rho}{\partial \theta}=\sum_{s} d^{\pi}(s) \sum_{a} \frac{\partial \pi(s, a)}{\partial \theta} Q^{\pi}(s, a) \]
因此,PG定理等价于\(L_{\theta_{old}}\)的一阶近似的梯度在\(\theta\) 空间 \(l_2\) 约束下的优化问题,即18式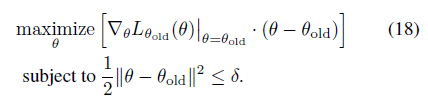
7.3 近似数值解法
这里简单描述关于17式及其参数更新规则中的大矩阵数值计算近似方式。
$ {D}_{}^{} $ 二阶近似中的 \(A\) 是 Hessian 方形矩阵,维度为 \(\theta\) 个数的平方。
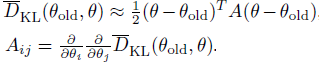
直接构建 \(A\) 矩阵或者其逆矩阵 \(A^{-1}\)都是计算量巨大的, 注\(A^{-1}\)出现在natural policy update \(\theta\) 更新公式中,\(A^{-1} \nabla_{\theta} L(\theta)\) 。
一种方法是通过构建Fisher Information Matrix,引入期望形式便于采样 \[ \mathbf{A}=E_{\pi_{\theta}}\left[\nabla_{\theta} \log \pi_{\theta}(\mathbf{a} \mid \mathbf{s}) \nabla_{\theta} \log \pi_{\theta}(\mathbf{a} \mid \mathbf{s})^{T}\right] \] 另一种方式是使用conjugate gradient 方法,通过矩阵乘以向量快速计算法迭代逼近 \(A^{-1} \nabla_{\theta} L(\theta)\)。
8. 试验结果
在两种强化学习模式下,比较TRPO和其他模型的效果。模式一是在MuJoCo模拟器中,这种环境下能得到真实状态的情况。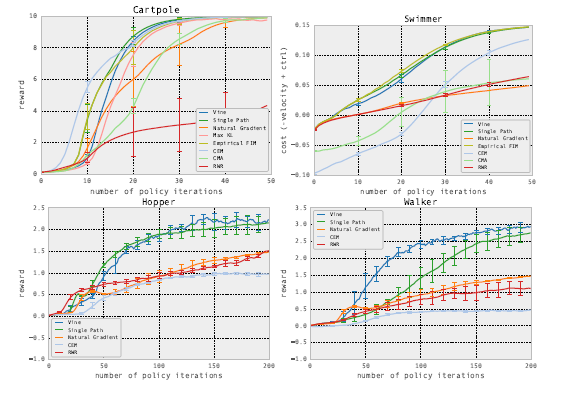
另一种模式是完全信息下的Atari游戏环境,这种环境下观察到的屏幕像素可以信息完全地表达潜在真实状态。
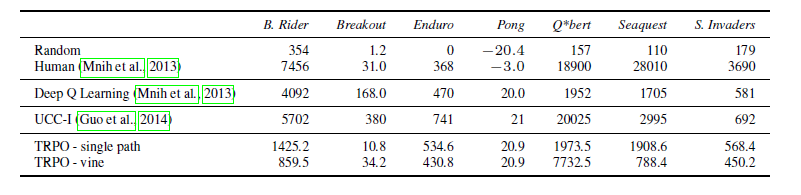

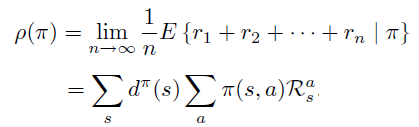
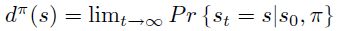
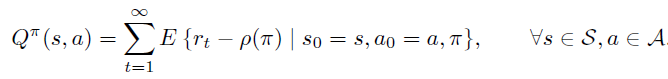
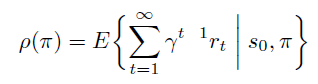
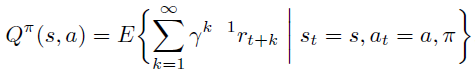
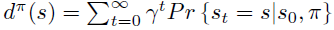
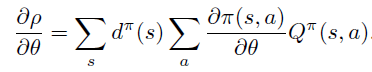
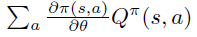
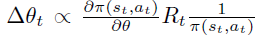
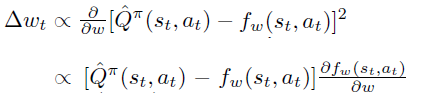
.png)