深入 LeetCode 470 拒绝采样，状态转移图求期望和一道经典统计求期望题目

在这篇文章中，我们从一道LeetCode 470 题目出发，通过系统地思考，引出拒绝采样（Reject Sampling）的概念，并探索比较三种拒绝采样地解法；接着借助状态转移图来定量计算采样效率；最后，我们利用同样的方法来解一道稍微复杂些的经典抛硬币求期望的统计面试题目。

Leetcode 470 用 Rand7() 实现 Rand10()

已有方法 rand7 可生成 1 到 7 范围内的均匀随机整数，试写一个方法 rand10 生成 1 到 10 范围内的均匀随机整数。

不要使用系统的 Math.random() 方法。

思考

• rand7()调用次数的 期望值 是多少 ?

• 你能否尽量少调用 rand7() ?

思维过程

我们已有 rand7() 等概率生成了 [1, 7] 中的数字，我们需要等概率生成 [1, 10] 范围内的数字。第一反应是调用一次rand7() 肯定是不够的，因为覆盖的范围不够。那么，就需要至少2次调用 rand7() 才能生成一次 rand10()，但是还要保证 [1, 10] 的数字生成概率相等，这个是难点。 现在我们先来考虑反问题，给定rand10() 生成 rand7()。这个应该很简单，调用一次 rand10() 得到 [1, 10]，如果是 8, 9, 10 ，则丢弃，重新开始，否则返回。想必大家都能想到这个朴素的方法，这种思想就是统计模拟中的拒绝采样（Reject Sampling）。

有了上面反问题的思考，我们可能会想到，rand7() 可以生成 rand5()，覆盖 [1, 5]的范围，如果将区间 [1, 10] 分成两个5个值的区间 [1, 5] 和 [6, 10]，那么 rand7() 可以通过先等概率选择区间 [1, 5] 或 [6, 10]，再通过rand7() 生成 rand5()就可以了。这个问题就等价于先用 rand7() 生成 rand2()，决定了 [1, 5] 还是 [6, 10]，再通过rand7() 生成 rand5() 。

解法一：rand2() + rand5()

我们来实现这种解法。下图为调用两次 rand7() 生成 rand10 数值的映射关系：横轴表示第一次调用，1，2，3决定选择区间 [1, 5] ，4，5，6选择区间 [6, 10]。灰色部分表示结果丢弃，重新开始 （注，若第一次得到7无需再次调用 rand7()）。

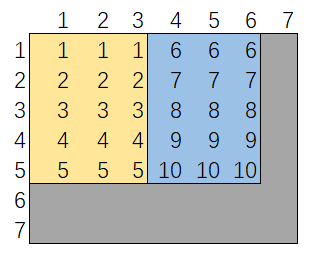
有了上图，我们很容易写出如下 AC 代码。

{linenos

# AC
# Runtime: 408 ms, faster than 23.80% of Python3 online submissions for Implement Rand10() Using Rand7().
# Memory Usage: 16.7 MB, less than 90.76% of Python3 online submissions for Implement Rand10() Using Rand7().
class Solution:
    def rand10(self):
        while True:
            a = rand7()
            if a <= 3:
                b = rand7()
                if b <= 5:
                    return b
            elif a <= 6:
                b = rand7()
                if b <= 5:
                    return b + 5

标准解法：rand49()

从提交的结果来看，第一种解法慢于多数解法。原因是我们的调用 rand7() 的采样效率比较低，第一次有 1/7 的概率结果丢弃，第二次有 2/7的概率被丢弃。

如何在第一种解法的基础上提高采样效率呢？直觉告诉我们一种做法是降低上述 7x7 表格中灰色格子的面积。此时，会想到我们通过两次 rand7() 已经构建出来 rand49()了，那么再生成 rand10() 也规约成基本问题了。

下图为 rand49() 和 rand10() 的数字对应关系。

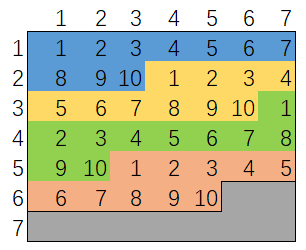
实现代码比较简单。注意，while True 可以去掉，用递归来代替。

{linenos

# AC
# Runtime: 376 ms, faster than 54.71% of Python3 online submissions for Implement Rand10() Using Rand7().
# Memory Usage: 16.9 MB, less than 38.54% of Python3 online submissions for Implement Rand10() Using Rand7().
class Solution:
    def rand10(self):
        while True:
            a, b = rand7(),  rand7()
            num = (a - 1) * 7 + b
            if num <= 40:
                return num % 10 + 1

更快的做法

上面的提交结果发现标准解法在运行时间上有了不少提高，处于中等位置。我们继续思考，看看能否再提高采样效率。

观察发现，rand49() 有 9/49 的概率，生成的值被丢弃，原因是 [41, 49] 只有 9 个数，不足10个。倘若此时能够将这种状态保持下去，那么只需再调用一次 rand7() 而不是从新开始情况下至少调用两次 rand7()， 就可以得到 rand10()了。也就是说，当 rand49() 生成了 [41, 49] 范围内的数的话等价于我们先调用了一次 rand9()，那么依样画葫芦，我们接着调用 rand7() 得到了 rand63()。63 分成了6个10个值的区间后，剩余 3 个数。此时，又等价于 rand3()，循环往复，调用了 rand7() 得到了 rand21()，最后若rand21() 不幸得到21，等价于 rand1()，此时似乎我们走投无路，只能回到最初的状态，一切从头再来了。

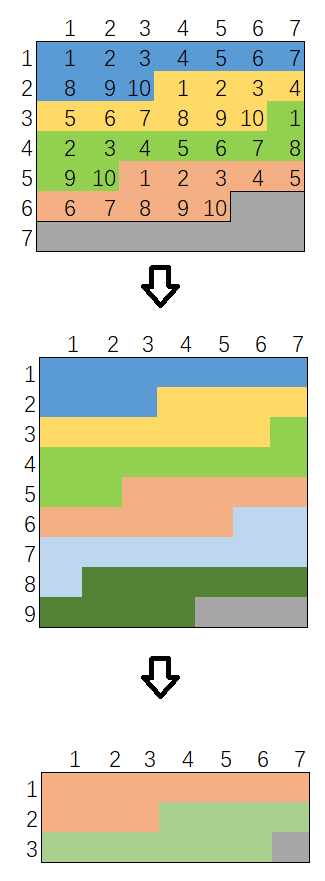
改进算法代码如下。注意这次击败了 92.7%的提交。

{linenos

# AC
# Runtime: 344 ms, faster than 92.72% of Python3 online submissions for Implement Rand10() Using Rand7().
# Memory Usage: 16.7 MB, less than 90.76% of Python3 online submissions for Implement Rand10() Using Rand7().
class Solution:
    def rand10(self):
        while True:
            a, b = rand7(),  rand7()
            num = (a - 1) * 7 + b
            if num <= 40: return num % 10 + 1
            a = num - 40
            b = rand7()
            num = (a - 1) * 7 + b
            if num <= 60: return num % 10 + 1
            a = num - 60
            b = rand7()
            num = (a - 1) * 7 + b
            if num <= 20: return num % 10 + 1

采样效率计算

通过代码提交的结果和大致的分析，我们已经知道三个解法在采样效率依次变得更快。现在我们来定量计算这三个解法。

我们考虑生成一个 rand10() 平均需要调用多少次 rand7()，作为采样效率的标准。

一种思路是可以通过模拟方法，即将上述每个解法模拟多次，然后用总的 rand7() 调用次数除以 rand10() 的生成次数即可。下面以解法三为例写出代码

{linenos

# The rand7() API is already defined for you.
rand7_c = 0
rand10_c = 0

def rand7():
    global rand7_c
    rand7_c += 1
    import random
    return random.randint(1, 7)
    
def rand10():
    global rand10_c
    rand10_c += 1
    while True:
        a, b = rand7(), rand7()
        num = (a - 1) * 7 + b
        if num <= 40: return num % 10 + 1
        a = num - 40   # [1, 9]
        b = rand7()
        num = (a - 1) * 7 + b  # [1, 63]
        if num <= 60: return num % 10 + 1
        a = num - 60  # [1, 3]
        b = rand7()
        num = (a - 1) * 7 + b  # [1, 21]
        if num <= 20: return num % 10 + 1

if __name__ == '__main__':
    while True:
        rand10()
        print(f'{rand10_c} {round(rand7_c/rand10_c, 2)}')

运行代码，发现解法三的采样效率稳定在 2.19。

采样效率精确计算

计算解法二

为了精确计算三个解法的采样效率，我们通过代码得到对应的状态转移图来帮助计算。

例如，解法一可以对应到下图：初始状态 Start 节点中的 +2 表示经过此节点会产生 2次 rand7() 的代价。从 Start 节点有 40/49 的概率到达被接受状态 AC，有 9/49 概率到达拒绝状态 REJ。REJ 需要从头开始，则用虚线表示重新回到 Start节点，也就是说 REJ 的代价等价于 Start。注意，从某个节点出发的所有边之和为1。

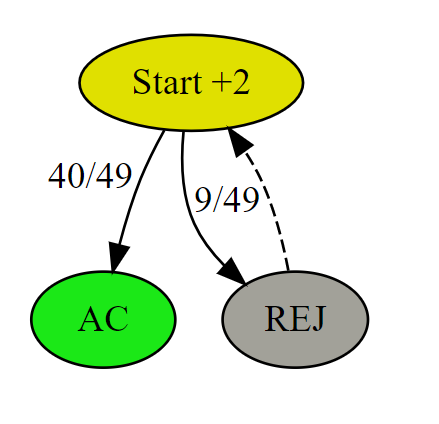
有了上述状态转移关系图，我们令初始状态的平均代价为 \(C_2\)，则可以写成递归表达式，因为其中 REJ 的代价就是 \(C_2\)，即

\[ C_2 = 2 + (\frac{40}{49}\cdot0 + \frac{9}{49} C_2) \]

解得 \(C_2\)

\[ C_2 = 2.45 \]

计算解法一

同样的，对于另外两种解法，虽然略微复杂，也可以用同样的方法求得。

解法一的状态转移图为

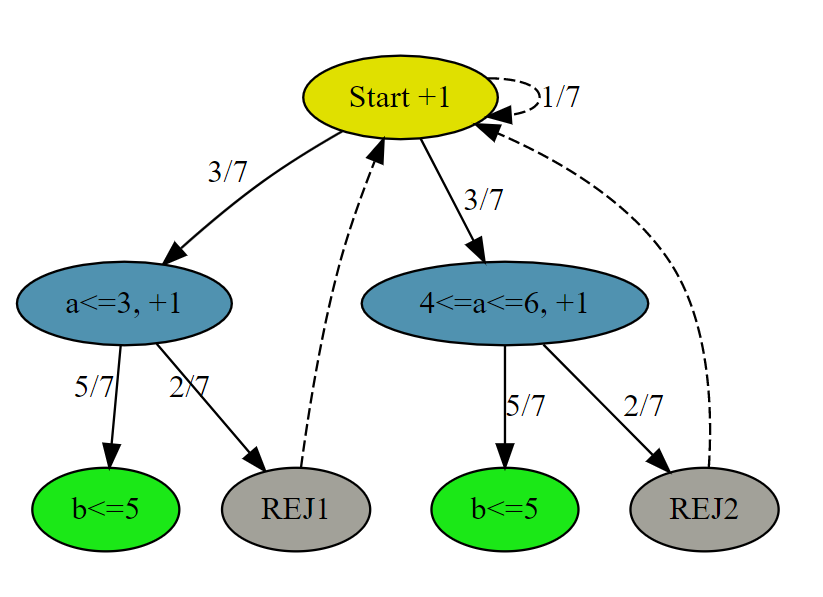
递归方程表达式为

\[ C_1 = 1+\frac{3}{7} \cdot (1+\frac{5}{7} \cdot 0 + \frac{2}{7} \cdot C_1) \cdot2+ \frac{1}{7} \cdot (C_1) \]

解得 \(C_1\)

\[ C_1 = \frac{91}{30} \approx 3.03 \]

计算解法三

最快的解法三状态转移图为

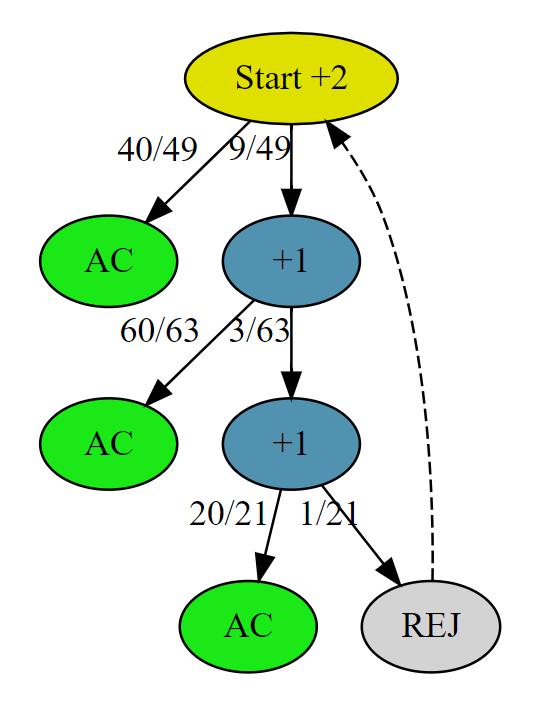
递归方程表达式为

\[ C_3 = 2+\frac{40}{49} \cdot 0 + \frac{9}{49} (1+\frac{60}{63} \cdot 0 + \frac{3}{63} \cdot (1+\frac{20}{21} \cdot 0 + \frac{1}{21} \cdot C_3)) \]

解得 \(C_3\) \[ C_3 = \frac{329}{150} \approx 2.193 \]

至此总结一下，三个解法的平均代价为 \[ C_1 \approx 3.03 > C_2 = 2.45 > C_3 \approx 2.193 \] 这些值和我们通过模拟得到的结果一致。

稍难些的经典概率求期望题目

至此，LeetCode 470 我们已经分析透彻。现在，我们已经可以很熟练的将此类拒绝采样的问题转变成有概率的状态转移图，再写成递推公式去求平均采样的代价（即期望）。这里，如果大家感兴趣的话不妨再来看一道略微深入的经典统计概率求期望的题目。

问题：给定一枚抛正反面概率一样的硬币，求连续抛硬币直到两个正面（正面记为H，两个正面HH）的平均次数。例如：HTTHH是一个连续次数为5的第一次出现HH的序列。

分析问题画出状态转移图：我们令初始状态下得到第一个HH的平均长度记为 S，那么下一次抛硬币有 1/2 机会是 T，此时状态等价于初始状态，另有 1/2 机会是 H，我们记这个状态下第一次遇见HH的平均长度为 H（下图蓝色节点）。从此蓝色节点出发，当下一枚硬币是H则结束，是T是返回初始状态。于是构建出下图。

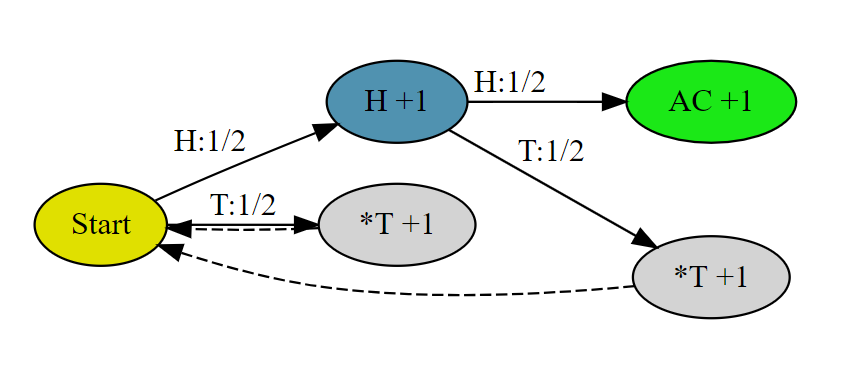
这个问题稍微复杂的地方在于我们有两个未知状态互相依赖，但问题的本质和方法是一样的，分别从 S 和 H 出发考虑状态的概率转移，可以写成如下两个方程式：

\[ \left\{ \begin{array}{c} S =&\frac{1}{2} \cdot(1+H) + \frac{1}{2} \cdot(1+S) \\ H =&\frac{1}{2} \cdot 1 + \frac{1}{2} \cdot(1+S) \end{array} \right. \]

解得

\[ \left\{ \begin{array}{c} H= 4 \\ S = 6 \end{array} \right. \]

因此，平均下来，需要6次抛硬币才能得到 HH，这个是否和你直觉的猜测一致呢？

这个问题还可以有另外一问，可以作为思考题让大家来练习一下：第一次得到 HT 的平均次数是多少？这个是否和 HH 一样呢？