Leetcode 1227 是一道有意思的概率题,本篇将从多个角度来讨论这道题。题目如下
有 n 位乘客即将登机,飞机正好有 n 个座位。第一位乘客的票丢了,他随便选了一个座位坐下。 剩下的乘客将会: 如果他们自己的座位还空着,就坐到自己的座位上, 当他们自己的座位被占用时,随机选择其他座位,第 n 位乘客坐在自己的座位上的概率是多少?
示例 1: 输入:n = 1 输出:1.00000 解释:第一个人只会坐在自己的位置上。
示例 2: 输入: n = 2 输出: 0.50000 解释:在第一个人选好座位坐下后,第二个人坐在自己的座位上的概率是 0.5。
提示: 1 <= n <= 10^5
假设规模为n时答案为f(n),一般来说,这种递推问题在数学形式上可能有关于n的简单数学表达式(closed form),或者肯定有f(n)关于f(n-k)的递推表达式。工程上,我们可以通过通过多次模拟即蒙特卡罗模拟来算得近似的数值解。
Monte Carlo 模拟发现规律
首先,我们先来看看如何高效的用代码来模拟。根据题意的描述过程,直接可以写出下面代码。seats为n大小的bool 数组,每个位置表示此位置是否已经被占据。然后依次给第i个人按题意分配座位。注意,每次参数随机数范围在[0,n-1],因此,会出现已经被占据的情况,此时需要再次随机,直至分配到空位。
暴力直接模拟
1 | def simulate_bruteforce(n: int) -> bool: |
运行上面的代码来模拟 n 从 2 到10 的情况,每种情况跑500次模拟,输出如下
1 | 1 => 1.0 |
发现当 n>=2 时,似乎概率都是0.5。
标准答案
其实,这道题的标准答案就是 n=1 为1,n>=2 为0.5。下面是 python 3 标准答案。本篇后面会从多个角度来探讨为什么是0.5 。
1 | class Solution: |
O(n) 改进算法
上面的暴力直接模拟版本有个最大的问题是当n很大时,随机分配座位会产生大量冲突,因此,最坏复杂度是没有任何上限的。解决方法是每次发生随机分配时保证不冲突,能直接选到空位。下面是一种最坏复杂度O(n)的模拟过程,seats数组初始话成 0,1,...,n-1,表示座位号。当第i个人登机时,seats[i:n] 的值为他可以选择的座位集合,而seats[0:i]为已经被占据的座位集合。由于[i: n]是连续空间,产生随机数就能保证不冲突。当第i个人选完座位时,将他选中的seats[k]和seats[i] 交换,保证第i+i个人面临的seats[i+1:n]依然为可选座位集合。
1 | def simulate_online(n: int) -> bool: |
递推思维
这一节我们用数学递推思维来解释0.5的解。令f(n) 为第 n 位乘客坐在自己的座位上的概率,考察第一个人的情况(first step analysis),有三种可能
- 第一个人选了第一个即自己的座位,那么最后一个人一定能保证坐在自己的座位。
- 第一个人选了最后一个人的座位,无论中间什么过程,最后一个人无法坐到自己座位
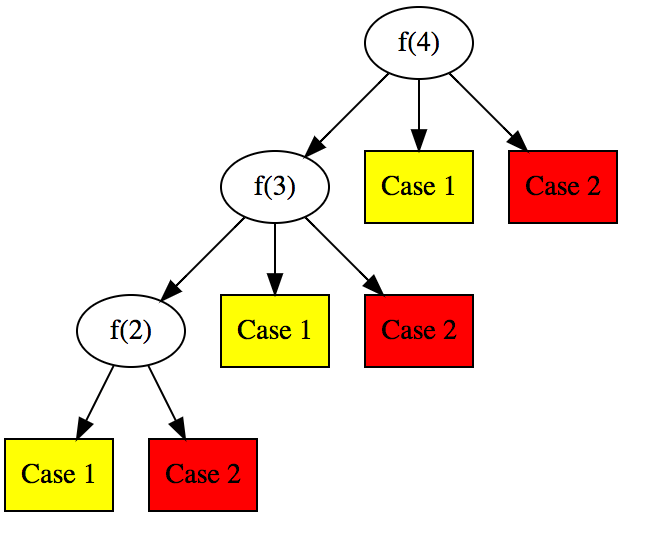
- 第一个人选了第i个座位,(1<i<n),那么第i个人前面的除了第一个外的人都会坐在自己位置上,第i个人由于没有自己座位,随机在剩余的座位1,座位 [i+1,n] 中随机选择,此时,问题转变为f(n-i+1),如下图所示。
.png)
.png)
通过上面分析,得到概率递推关系如下
\[ f(n) = \begin{align*} \left\lbrace \begin{array}{r@{}l} 1 & & p=\frac{1}{n} \quad \text{选了第一个位置} \\\\\\ f(n-i+1) & & p=\frac{1}{n} \quad \text{选了第i个位置,1<i<n} \\\\\\ 0 & & p=\frac{1}{n} \quad \text{选了第n个位置} \end{array} \right. \end{align*} \]
即f(n)的递推式为: \[ f(n) = \frac{1}{n} + \frac{1}{n} \times [ f(n-1) + f(n-2) + ...+ f(2)], \quad n>=2 \] 同理,f(n+1)递推式如下 \[ f(n+1) = \frac{1}{n+1} + \frac{1}{n+1} \times [ f(n) + f(n-1) + ...+ f(2)] \] \((n+1)f(n+1) - nf(n)\) 抵消 \(f(n-1) + ...f(2)\) 项,可得 \[ (n+1)f(n+1) - nf(n) = f(n) \] 即 \[ f(n+1) = f(n) = \frac{1}{2} \quad n>=2 \]
用数学归纳法也可以证明 n>=2 时 f(n)=0.5。
简化的思考方式
我们再仔细思考一下上面的第三种情况,就是第一个人坐了第i个座位,1<i<n,此时,程序继续,不产生结果,直至产生结局1或者2,也就是case 1和2是真正的结局节点,它们产生的概率相同,因此答案是1/2。
从调用图可以看出这种关系,由于中间节点 f(4),f(3),f(2)生成Case 1和2的概率一样,因此无论它们之间是什么关系,最后结果都是1/2.
知乎上有个很形象的类比理解方式
考虑一枚硬币,正面向上的概率为 1/n,反面也是,立起来的概率为 (n-2)/n 。我们规定硬币立起来重新抛,但重新抛时,n会至少减小1。求结果为反面的概率。这样很显然结果为 1/2 。
这里,正面向上对应Case 2,反面对应Case 1。
这种思想可以写出如下代码,seats为 n 大小的bool 数组,当第i个人(0<i<n)发现自己座位被占的话,此时必然seats[0]没有被占,同时seats[i+1:]都是空的。假设seats[0]被占的话,要么是第一个人占的,要么是第p个人(p<i)坐了,两种情况下乱序都已经恢复了,此时第i个座位一定是空的。
1 | def simulate(n: int) -> bool: |

评论
shortnamefor Disqus. Please set it in_config.yml.