Leetcode矩阵快速幂运算解法

Tech Blog 15 分钟 读完 (约 2259 字)

快速幂运算是一种利用位运算和DP思想求的\(x^n\)的数值算法，它将时间复杂度\(O(n)\)降到\(O(log(n))\)。快速幂运算结合矩阵乘法，可以巧解不少DP问题。本篇会由浅入深，从最基本的快速幂运算算法，到应用矩阵快速幂运算解DP问题，结合三道Leetcode题目来具体讲解。

Leetcode 50. Pow(x, n) (Medium)

Leetcode 50. Pow(x, n) 是实数的快速幂运算问题，题目如下。

Implement pow(x, n), which calculates x raised to the power n (i.e. \(x^n\)).

Example 1:

1
2
Input: x = 2.00000, n = 10
Output: 1024.00000

Example 2:

1
2
Input: x = 2.10000, n = 3
Output: 9.26100

Example 3:

1
2
3
Input: x = 2.00000, n = -2
Output: 0.25000
Explanation: 2-2 = 1/22 = 1/4 = 0.25

快速幂运算解法分析

假设n是32位的int类型，将n写成二进制形式，那么n可以写成最多32个某位为 1（第k位为1则值为\(2^k\)）的和。那么\(x^n\)最多可以由32个 \(x^{2^k}\)的乘积组合，例如：

\[ x^{\text{10011101}_{2}} = x^{1} \times x^{\text{100}_{2}} \times x^{\text{1000}_{2}} \times x^{\text{10000}_{2}} \times x^{\text{10000000}_{2}} \]

快速幂运算的特点就是通过32次循环，每次循环根据上轮\(x^{2^k}\)的值进行平方后得出这一轮的值：\(x^{2^k} \times x^{2^k} = x^{2^{k+1}}\)，即循环计算出如下数列

\[ x^{1}, x^2=x^{\text{10}_{2}}, x^4=x^{\text{100}_{2}}, x^8=x^{\text{1000}_{2}}, x^{16}=x^{\text{10000}_{2}}, ..., x^{128} = x^{\text{10000000}_{2}} \]

在循环时，如果n的二进制形式在本轮对应的位的值是1，则将这次结果累乘计入最终结果。

下面是python 3 的代码，由于循环为32次，所以容易看出算法复杂度为 \(O(log(n))\)。

{linenos
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# AC
# Runtime: 32 ms, faster than 54.28% of Python3 online submissions for Pow(x, n).
# Memory Usage: 14.2 MB, less than 5.04% of Python3 online submissions for Pow(x, n).

class Solution:
    def myPow(self, x: float, n: int) -> float:
        ret = 1.0
        i = abs(n)
        while i != 0:
            if i & 1:
                ret *= x
            x *= x
            i = i >> 1
        return 1.0 / ret if n < 0 else ret

对应的 Java 的代码。

{linenos
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// AC
// Runtime: 1 ms, faster than 42.98% of Java online submissions for Pow(x, n).
// Memory Usage: 38.7 MB, less than 48.31% of Java online submissions for Pow(x, n).

class Solution {
    public double myPow(double x, int n) {
        double ret = 1.0;
        long i = Math.abs((long) n);
        while (i != 0) {
            if ((i & 1) > 0) {
                ret *= x;
            }
            x *= x;
            i = i >> 1;
        }

        return n < 0 ? 1.0 / ret : ret;
    }
}

矩阵快速幂运算

快速幂运算也可以应用到计算矩阵的幂，即上面的x从实数变为方形矩阵。实现上，矩阵的幂需要矩阵乘法：$ A_{r c} B_{c p}$ ，Python中可以用numpy的 np.matmul(A, B)来完成，而Java版本中我们手动实现简单的矩阵相乘算法，从三重循环看出其算法复杂度为\(O(r \times c \times p)\)。

{linenos
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public int[][] matrixProd(int[][] A, int[][] B) {
    int R = A.length;
    int C = B[0].length;
    int P = A[0].length;
    int[][] ret = new int[R][C];
    for (int r = 0; r < R; r++) {
        for (int c = 0; c < C; c++) {
            for (int p = 0; p < P; p++) {
                ret[r][c] += A[r][p] * B[p][c];
            }
        }
    }
    return ret;
}

Leetcode 509. Fibonacci Number (Easy)

有了快速矩阵幂运算，我们来看看如何具体解题。Fibonacci问题作为最基本的DP问题，在上一篇Leetcode 679 24 Game 的 Python 函数式实现中我们用python独有的yield来巧解，这次再拿它来做演示。

The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,

1
2
F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), for N > 1.

Given N, calculate F(N).

Example 1:

1
2
3
Input: 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.

Example 2:

1
2
3
Input: 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.

Example 3:

1
2
3
Input: 4
Output: 3
Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.

转换为矩阵幂运算

Fibonacci的二阶递推式如下：

\[ \begin{align*} F(n) =& F(n-1) + F(n-2) \\ F(n-1) =& F(n-1) \end{align*} \]

等价的矩阵递推形式为：

\[ \begin{bmatrix}F(n)\\F(n-1)\end{bmatrix} = \begin{bmatrix}1 & 1\\1 & 0\end{bmatrix} \begin{bmatrix}F(n-1)\\F(n-2)\end{bmatrix} \]

也就是每轮左乘一个2维矩阵。其循环形式为，即矩阵幂的形式：

\[ \begin{bmatrix}F(n)\\F(n-1)\end{bmatrix} = \begin{bmatrix}1 & 1\\1 & 0\end{bmatrix}^{n-1} \begin{bmatrix}F(1)\\F(0)\end{bmatrix} \]

AC代码

有了上面的矩阵幂公式，代码稍作改动即可。Java 版本代码。

{linenos
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * AC
 * Runtime: 0 ms, faster than 100.00% of Java online submissions for Fibonacci Number.
 * Memory Usage: 37.9 MB, less than 18.62% of Java online submissions for Fibonacci Number.
 *
 * Method: Matrix Fast Power Exponentiation
 * Time Complexity: O(log(N))
 **/
class Solution {
    public int fib(int N) {
        if (N <= 1) {
            return N;
        }
        int[][] M = {{1, 1}, {1, 0}};
        // powers = M^(N-1)
        N--;
        int[][] powerDouble = M;
        int[][] powers = {{1, 0}, {0, 1}};
        while (N > 0) {
            if (N % 2 == 1) {
                powers = matrixProd(powers, powerDouble);
            }
            powerDouble = matrixProd(powerDouble, powerDouble);
            N = N / 2;
        }

        return powers[0][0];
    }

    public int[][] matrixProd(int[][] A, int[][] B) {
        int R = A.length;
        int C = B[0].length;
        int P = A[0].length;
        int[][] ret = new int[R][C];
        for (int r = 0; r < R; r++) {
            for (int c = 0; c < C; c++) {
                for (int p = 0; p < P; p++) {
                    ret[r][c] += A[r][p] * B[p][c];
                }
            }
        }
        return ret;
    }

}

Python 3的numpy.matmul() 版本代码。

{linenos
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# AC
# Runtime: 256 ms, faster than 26.21% of Python3 online submissions for Fibonacci Number.
# Memory Usage: 29.4 MB, less than 5.25% of Python3 online submissions for Fibonacci Number.

class Solution:

    def fib(self, N: int) -> int:
        if N <= 1:
            return N

        import numpy as np
        F = np.array([[1, 1], [1, 0]])

        N -= 1
        powerDouble = F
        powers = np.array([[1, 0], [0, 1]])
        while N > 0:
            if N % 2 == 1:
                powers = np.matmul(powers, powerDouble)
            powerDouble = np.matmul(powerDouble, powerDouble)
            N = N // 2

        return powers[0][0]

或者也可以直接调用numpy.matrix_power() 代替手动的快速矩阵幂运算。

{linenos
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# AC
# Runtime: 116 ms, faster than 26.25% of Python3 online submissions for Fibonacci Number.
# Memory Usage: 29.2 MB, less than 5.25% of Python3 online submissions for Fibonacci Number.

class Solution:

    def fib(self, N: int) -> int:
        if N <= 1:
            return N

        from numpy.linalg import matrix_power
        import numpy as np
        F = np.array([[1, 1], [1, 0]])
        F = matrix_power(F, N - 1)

        return F[0][0]

Leetcode 1411. Number of Ways to Paint N × 3 Grid (Hard)

下面来看一道稍难一点的DP问题，1411. Number of Ways to Paint N × 3 Grid。

You have a grid of size n x 3 and you want to paint each cell of the grid with exactly one of the three colours: Red, Yellow or Green while making sure that no two adjacent cells have the same colour (i.e no two cells that share vertical or horizontal sides have the same colour).

You are given n the number of rows of the grid.

Return the number of ways you can paint this grid. As the answer may grow large, the answer must be computed modulo 10^9 + 7.

Example 1:

1
2
3
Input: n = 1
Output: 12
Explanation: There are 12 possible way to paint the grid as shown:

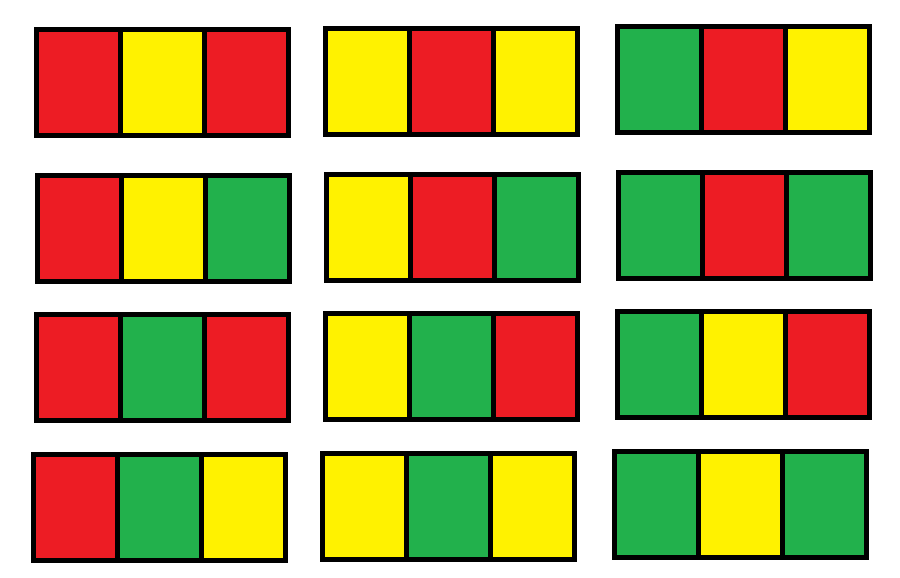
Example 2:

1
2
Input: n = 2
Output: 54

Example 3:

1
2
Input: n = 3
Output: 246

Example 4:

1
2
Input: n = 7
Output: 106494

Example 5:

1
2
Input: n = 5000
Output: 30228214

标准DP解法

分析题目容易发现第i行的状态只取决于第i-1行的状态，第i行会有两种不同状态：三种颜色都有或者只有两种颜色。这个问题容易识别出是经典的双状态DP问题，那么我们定义dp2[i]为第i行只有两种颜色的数量，dp3[i]为第i行有三种颜色的数量。

先考虑dp3[i]和i-1行的关系。假设第i行包含3种颜色，即dp3[i]，假设具体颜色为红，绿，黄，若i-1行包含两种颜色（即dp2[i-1]），此时dp2[i-1]只有以下2种可能：

dp2[i-1] -> dp3[i]
还是dp3[i] 红，绿，黄情况，若i-1行包含三种颜色（从dp3[i-1]转移过来），此时dp3[i-1]也只有以下2种可能：
dp3[i-1] -> dp3[i]

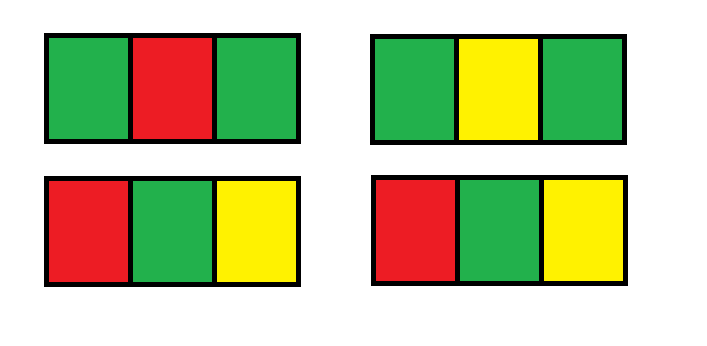
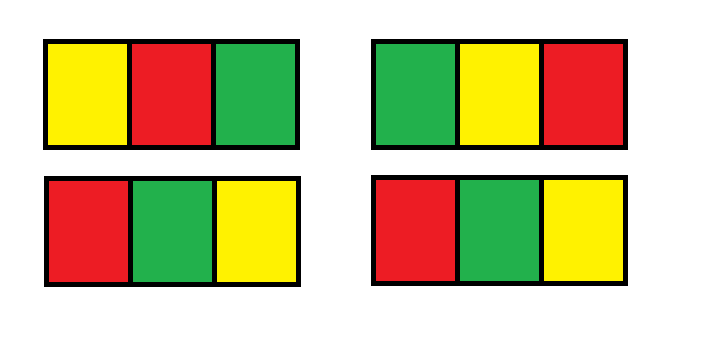
因此，dp3[i]= dp2[i-1] * 2 + dp3[i-1] * 2。

同理，若第i行包含两种颜色，即dp2[i]，假设具体颜色为绿，黄，绿，若i-1行是两种颜色（dp2[i-1]），此时dp2[i-1]有如下3种可能：

dp2[i-1] -> dp2[i]
dp2[i]的另一种情况是由dp3[i-1]转移过来，则dp3[i-1]有2种可能，枚举如下：
dp3[i-1] -> dp2[i]

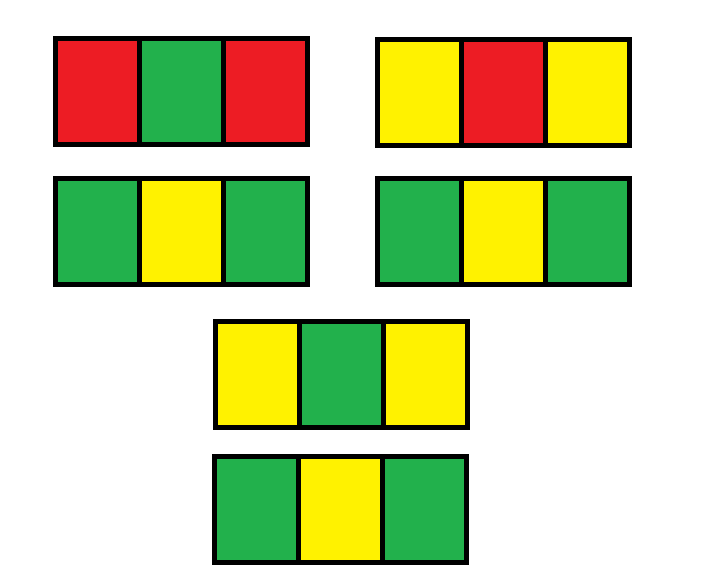
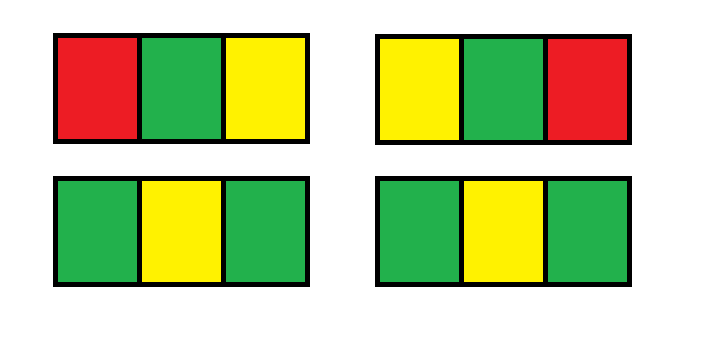
因此，dp2[i] = dp2[i-1] * 3 + dp3[i-1] * 2。 初始值dp2[1] = 6，dp3[1] = 6，最终答案为dp2[i] + dp3[i]。

很容易写出普通DP版本的Python 3代码，时间复杂度为\(O(n)\)。

{linenos
1
2
3
4
5
6
7
8
9
10
11
12
13
# AC
# Runtime: 36 ms, faster than 98.88% of Python3 online submissions for Number of Ways to Paint N × 3 Grid.
# Memory Usage: 13.9 MB, less than 58.66% of Python3 online submissions for Number of Ways to Paint N × 3 Grid.

class Solution:
    def numOfWays(self, n: int) -> int:
        MOD = 10 ** 9 + 7
        dp2, dp3 = 6, 6
        n -= 1
        while n > 0:
            dp2, dp3 = (dp2 * 3 + dp3 * 2) % MOD, (dp2 * 2 + dp3 * 2) % MOD
            n -= 1
        return (dp2 + dp3) % MOD

快速矩阵幂运算解法

和Fibonacci一样，我们将DP状态转移方程转换成矩阵乘法：

\[ \begin{bmatrix}dp2(n)\\dp3(n)\end{bmatrix} = \begin{bmatrix}3 & 2\\2 & 2\end{bmatrix} \begin{bmatrix}dp2(n-1)\\dp3(n-1)\end{bmatrix} \]

代入初始值，转换成矩阵幂形式

\[ \begin{bmatrix}dp2(n)\\dp3(n)\end{bmatrix} = \begin{bmatrix}3 & 2\\2 & 2\end{bmatrix}^{n-1}\begin{bmatrix}6\\6\end{bmatrix} \]

代码几乎和Fibonacci一模一样，仅仅多了mod 计算。下面是Java版本。

{linenos
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

/**
AC
Runtime: 0 ms, faster than 100.00% of Java online submissions for Number of Ways to Paint N × 3 Grid.
Memory Usage: 35.7 MB, less than 97.21% of Java online submissions for Number of Ways to Paint N × 3 Grid.
**/

class Solution {
    public int numOfWays(int n) {
        long MOD = (long) (1e9 + 7);
        long[][] ret = {{6, 6}};
        long[][] m = {{3, 2}, {2, 2}};
        n -= 1;
        while(n > 0) {
            if ((n & 1) > 0) {
                ret = matrixProd(ret, m, MOD);
            }
            m = matrixProd(m, m, MOD);
            n >>= 1;
        }
        return (int) ((ret[0][0] + ret[0][1]) % MOD);

    }

    public long[][] matrixProd(long[][] A, long[][] B, long MOD) {
        int R = A.length;
        int C = B[0].length;
        int P = A[0].length;
        long[][] ret = new long[R][C];
        for (int r = 0; r < R; r++) {
            for (int c = 0; c < C; c++) {
                for (int p = 0; p < P; p++) {
                    ret[r][c] += A[r][p] * B[p][c];
                    ret[r][c] = ret[r][c] % MOD;
                }
            }
        }
        return ret;
    }

}

Python 3实现为

{linenos
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# AC
# Runtime: 88 ms, faster than 39.07% of Python3 online submissions for Number of Ways to Paint N × 3 Grid.
# Memory Usage: 30.2 MB, less than 11.59% of Python3 online submissions for Number of Ways to Paint N × 3 Grid.

class Solution:
    def numOfWays(self, n: int) -> int:
        import numpy as np

        MOD = int(1e9 + 7)
        ret = np.array([[6, 6]])
        m = np.array([[3, 2], [2, 2]])

        n -= 1
        while n > 0:
            if n % 2 == 1:
                ret = np.matmul(ret, m) % MOD
            m = np.matmul(m, m) % MOD
            n = n // 2
        return int((ret[0][0] + ret[0][1]) % MOD)
#Maths #Linear Algebra #Java #Python #Dynamic Programming #Leetcode
通过代码学Sutton强化学习：SARSA、Q-Learning和Expected SARSA时序差分算法训练CartPole 通过代码学Sutton强化学习4：21点游戏的蒙特卡洛On-Policy控制

Author and License Contact MyEncyclopedia to Authorize
myencyclopedia.top link https://blog.myencyclopedia.top/zh/2020/leetcode-matrix-power/
github.io link https://myencyclopedia.github.io/zh/2020/leetcode-matrix-power/

You need to set install_url to use ShareThis. Please set it in _config.yml.

评论

You forgot to set the shortname for Disqus. Please set it in _config.yml.
Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×