深度强化学习之：Policy Gradient Theorem 一些理解

Policy gradient 定理作为现代深度强化学习的基石，同时也是actor-critic的基础，重要性不言而喻。但是它的推导和理解不是那么浅显，不同的资料中又有着众多形式，不禁令人困惑。本篇文章MyEncyclopedia试图总结众多资料背后的一些相通的地方，并写下自己的一些学习理解心得。

引入 Policy Gradient

Policy gradient 引入的目的是若我们将策略 \(\pi_{\theta}\) 的参数 \(\theta\) 直接和一个标量 \(J\) 直接联系在一起的话，就能够利用目前最流行的深度学习自动求导的方法，迭代地去找到 \(\theta^*\) 来最大化 \(J\)：

\[ \theta^{\star}=\arg \max _{\theta} J(\theta) \]

\[ {\theta}_{t+1} \doteq {\theta}_{t}+\alpha \nabla J(\theta) \]

此时，训练神经网络成功地收敛到 \(\theta^{*}\) 时可以直接给出任意一个状态 s 的动作分布。

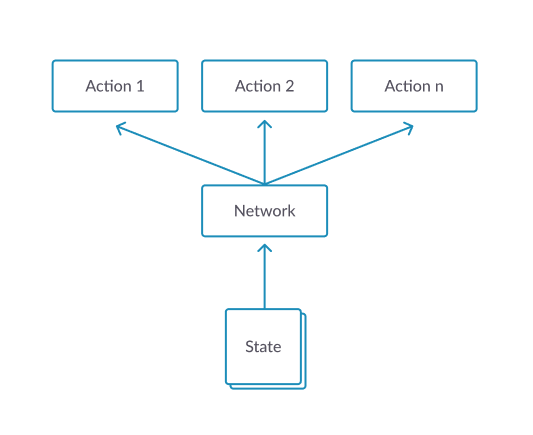
那么问题来了，首先一个如何定义 \(J(\theta)\)，其次，如何求出或者估计 $ J()$。

第一个问题比较直白，用value function或者广义的expected return都可以。

这里列举一些常见的定义。对于episodic 并且初始都是 \(s_0\)状态的情况，直接定义成v值，即Sutton教程中的episodic情况下的定义

\[ J(\boldsymbol{\theta}) \doteq v_{\pi_{\boldsymbol{\theta}}}\left(s_{0}\right) \quad \quad \text{(1.1)} \]

进一步，上式等价于 \(V(s)\) 在状态平稳分布下的均值。

\[ \begin{aligned} J(\theta) &= \sum_{s \in \mathcal{S}} d^{\pi}(s) V^{\pi}(s) \\ &=\sum_{s \in \mathcal{S}} d^{\pi}(s) \sum_{a \in \mathcal{A}} \pi_{\theta}(a \mid s) Q^{\pi}(s, a) \end{aligned} \quad \quad \text{(1.2)} \]

其中，状态平稳分布 \(d^{\pi}(s)\) 定义为

\[ d^{\pi}(s)=\lim _{t \rightarrow \infty} P\left(s_{t}=s \mid s_{0}, \pi_{\theta}\right) \]

另一种定义从trajectory角度出发，公式如下：

\[ J(\boldsymbol{\theta}) \doteq E_{\tau \sim p_{\theta}(\tau)}\left[\sum_{t} r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right] \quad \quad \text{(1.3)} \]

即$ $ 是一次trajectory，服从以 \(\theta\) 作为参数的随机变量

\[ \tau \sim p_{\theta}\left(\mathbf{s}_{1}, \mathbf{a}_{1}, \ldots, \mathbf{s}_{T}, \mathbf{a}_{T}\right) \]

\(J(\theta)\) 对于所有的可能的 \(\tau\) 求 expected return。这种视角下对于finite 和 infinite horizon来说也有变形。

Infinite horizon 情况下，通过 \((s, a)\) 的marginal distribution来计算

\[ J(\boldsymbol{\theta}) \doteq E_{(\mathbf{s}, \mathbf{a}) \sim p_{\theta}(\mathbf{s}, \mathbf{a})}[r(\mathbf{s}, \mathbf{a})] \quad \quad \text{(1.4)} \]

Finite horizon 情况下，通过每一时刻下 \((s_t, a_t)\) 的marginal distribution来计算

\[ J(\boldsymbol{\theta}) \doteq \sum_{t=1}^{T} E_{\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right) \sim p_{\theta}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)} \quad \quad \text{(1.5)} \]

关于第二个问题，如何求出或者估计 $ J()$ 就是 policy gradient theorem 的主题了。仔细想想确实会有一些问题。一是 reward 随机变量 \(R(s, a)\) 是离散情况下 $ J()$ 还是否存在，再是 \(J(\theta)\) 不仅取决于agent 主观的 \(\pi_{\theta}\)，还取决于环境客观的dynamics model

\[ p\left(s^{\prime}, r \mid s, a\right) = \operatorname{Pr}\left\{S_{t}=s^{\prime}, R_{t}=r \mid S_{t-1}=s, A_{t-1}=a\right\} \]

当环境dynamics未知时，如何再去求 $ J()$ 呢。还有就是如果涉及到状态的分布也是取决于环境dynamics的，计算 $ J()$ 也面临同样的问题。

幸好，policy gradient定理完美的解答了上述问题。我们先来看看它的表述内容。

Policy Gradient Theorem

策略梯度定理证明了，无论定义何种 \(J(\theta)\) ，策略梯度等比于下式，其中 \(\mu(s)\) 为 \(\pi_{\theta}\) 下的状态分布。等比系数在episodic情况下为episode的平均长度，在infinite horizon情况下为1。

\[ \nabla J(\boldsymbol{\theta}) \propto \sum_{s} \mu(s) \sum_{a} q_{\pi}(s, a) \nabla \pi(a \mid s, \boldsymbol{\theta}) \quad \quad \text{(2.1)} \]

考虑到系数可以包含在步长 \(\alpha\) 中， \(\mu(s)\) 是on policy \(\pi_{\theta}\) 的权重，\(\nabla J(\theta)\) 也可以写成期望形式的等式，注意，下式中 \(S_t\) 从具体 \(s\) 变成了随机变量，随机概率部分移到了 \(\mathbb{E}_{\pi}\)中了。

\[ \nabla J(\boldsymbol{\theta}) =\mathbb{E}_{\pi}\left[\sum_{a} q_{\pi}\left(S_{t}, a\right) \nabla \pi\left(a \mid S_{t}, \boldsymbol{\theta}\right)\right] \quad \quad \text{(2.2)} \]

Policy Gradient 定理的伟大之处在于等式右边并没有 \(d^{\pi}(s)\)，或者环境transition model \(p\left(s^{\prime}, r \mid s, a\right)\)！同时，等式右边变换成了最利于统计采样的期望形式，因为期望可以通过样本的平均来估算。

但是，这里必须注意的是action space的期望并不是基于 $(a S_{t}, ) $ 的权重的，因此，继续改变形式，引入 action space的 on policy 权重 $(a S_{t}, ) $ ，得到 2.3式。

\[ \nabla J(\boldsymbol{\theta})=\mathbb{E}_{\pi}\left[\sum_{a} \pi\left(a \mid S_{t}, \boldsymbol{\theta}\right) q_{\pi}\left(S_{t}, a\right) \frac{\nabla \pi\left(a \mid S_{t}, \boldsymbol{\theta}\right)}{\pi\left(a \mid S_{t}, \boldsymbol{\theta}\right)}\right] \quad \quad \text{(2.3)} \]

将 \(a\) 替换成 $A_{t} $，得到2.4式

\[ \nabla J(\boldsymbol{\theta})==\mathbb{E}_{\pi}\left[q_{\pi}\left(S_{t}, A_{t}\right) \frac{\nabla \pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}\right)}{\pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}\right)}\right] \quad \quad \text{(2.4)} \]

将 \(q_{\pi}\)替换成 \(G_t\)，由于

\[ \mathbb{E}_{\pi}[G_{t} \mid S_{t}, A_{t}]= q_{\pi}\left(S_{t}, A_{t}\right) \]

得到2.5式

\[ \nabla J(\boldsymbol{\theta})==\mathbb{E}_{\pi}\left[G_{t} \frac{\nabla \pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}\right)}{\pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}\right)}\right] \quad \quad \text{(2.5)} \]

至此，action 和 state space的权重都源自 \(\pi_{\theta}\)，期望内的随机变量可以通过 \(\pi_{\theta}\) 在每一时间 t 采样来无偏估计，这便是大名鼎鼎的 REINFORCE 算法，即Monte Carlo Policy Gradient。

\[ \nabla J(\boldsymbol{\theta}) \approx G_{t} \frac{\nabla \pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}\right)}{\pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}\right)} \quad \quad \text{(2.6)} \]

此时，\(\theta\) 迭代更新公式为

\[ \boldsymbol{\theta}_{t+1} \doteq \boldsymbol{\theta}_{t}+\alpha G_{t} \frac{\nabla \pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)}{\pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)} \quad \quad \text{(2.7)} \]

下面是REINFORCE算法完整流程

Policy Gradient Theorem - Trajectory Form

Trajectory 形式的策略梯度定理也很常见，这里也总结一下，回顾 1.3 式 \(J(\theta)\)的定义

\[ J(\boldsymbol{\theta}) \doteq E_{\tau \sim p_{\theta}(\tau)}\left[\sum_{t} r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right] \quad \quad \text{(1.3)} \]

最后可以证明出

\[ \nabla_{\theta} J\left(\pi_{\theta}\right)=\underset{\tau \sim \pi_{\theta}}{\mathrm{E}}\left[\sum_{t=0}^{T} \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right) R(\tau)\right] \quad \quad \text{(3.1)} \]

3.1式中每一时刻 t 中依赖全时刻的 \(R(\tau)\) ，进一步优化可以证明，时刻 t 只依赖于后续reward sum，即 reward-to-go， $ _{t}$

\[ \hat{R}_{t} \doteq \sum_{t^{\prime}=t}^{T} R\left(s_{t^{\prime}}, a_{t^{\prime}}, s_{t^{\prime}+1}\right) \]

最终的策略梯度定理的形式为：

\[ \nabla_{\theta} J\left(\pi_{\theta}\right)=\underset{\tau \sim \pi_{\theta}}{\mathrm{E}}\left[\sum_{t=0}^{T} \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right) \hat{R}_{t} \right] \quad \quad \text{(3.2)} \]

由于 log-derivative trick的存在，3.2式和2.5式（Sutton 教程中的policy gradient）等价。

\[ \nabla_{\theta} \log \pi_{\theta}(a)=\frac{\nabla_{\theta} \pi_{\theta}}{\pi_{\theta}} \quad \quad \text{(3.3)} \]

和监督学习的联系

Policy Gradient中的 \(\nabla_{\theta} \log \pi\) 广泛存在在机器学习范畴中，被称为 score function gradient estimator。RL 在supervised learning settings 中有 imitation learning，即通过专家的较优stochastic policy \(\pi_{\theta}(a|s)\) 收集数据集

\[ \{(s_1, a^{*}_1), (s_2, a^{*}_2), ...\} \]

算法有监督的学习去找到max log likelyhook 的 \(\theta^{*}\)

\[ \theta^{*}=\operatorname{argmax}_{\theta} \sum_{n} \log \pi_{\theta}\left(a_{n}^{*} \mid s_{n}\right) \quad \quad \text{(4.1)} \]

此时，参数迭代公式为

\[ \theta_{n+1} \leftarrow \theta_{n}+\alpha_{n} \nabla_{\theta} \log \pi_{\theta}\left(a_{n}^{*} \mid s_{n}\right) \quad \quad \text{(4.2)} \]

对照Policy Graident RL，on-policy \(\pi_{\theta}(a|s)\) 产生数据集

\[ \{(s_1, a_1, r_1), (s_2, a_2, r_2), ...\} \]

目标是最大化on-policy \(\pi_{\theta}\) 分布下的expected return

\[ \theta^{*}=\operatorname{argmax}_{\theta} \sum_{n} R(\tau_{n}) \]

对照2.7式 \(\theta\) 的更新公式，2.7式可以写成如下4.3式

\[ \theta_{n+1} \leftarrow \theta_{n}+\alpha_{n} G_{n} \nabla_{\theta} \log \pi_{\theta}\left(a_{n} \mid s_{n}\right) \quad \quad \text{(4.3)} \]

对比 4.3 和 4.2，发现此时4.3中只多了一个权重系数 \(G_n\)。

关于 $G_{n} {} {}(a_{n} s_{n}) $ 或者 \(G_{t} \frac{\nabla \pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)}{\pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)}\) 有一些深入的理解。

首先policy gradient RL 不像supervised imitation learning直接有label 作为signal，PG RL必须通过采样不同的action获得reward或者return作为signal，即1.4式中的

\[ E_{(\mathbf{s}, \mathbf{a}) \sim p_{\theta}(\mathbf{s}, \mathbf{a})}[r(\mathbf{s}, \mathbf{a})] \quad \quad \text{(5.1)} \]

广义的score function gradient estimator 对于形式为5.2的函数期望求gradient。对比上式，PG RL ， \(f(x)\)视为reward 随机变量，期望是under on-policy \(\pi_{\theta}\)。

\[ E_{x \sim p(x \mid \theta)}[f(x)] \quad \quad \text{(5.2)} \]

以下是score function gradient estimator的推导，这里不做赘述，主要利用了3.3式的 log-derivative trick。

\[ \begin{aligned} \nabla_{\theta} E_{x}[f(x)] &=\nabla_{\theta} \sum_{x} p(x) f(x) \\ &=\sum_{x} \nabla_{\theta} p(x) f(x) \\ &=\sum_{x} p(x) \frac{\nabla_{\theta} p(x)}{p(x)} f(x) \\ &=\sum_{x} p(x) \nabla_{\theta} \log p(x) f(x) \\ &=E_{x}\left[f(x) \nabla_{\theta} \log p(x)\right] \end{aligned} \quad \quad \text{(5.3)} \]

Policy Gradient 工作的机制大致如下

首先，根据现有的 on-policy \(\pi_{\theta}\) 采样出一些动作 action 产生trajectories，这些trajectories最终得到反馈 \(R(\tau)\)

用采样到的数据通过R加权来代替imitation learning的labeled loss

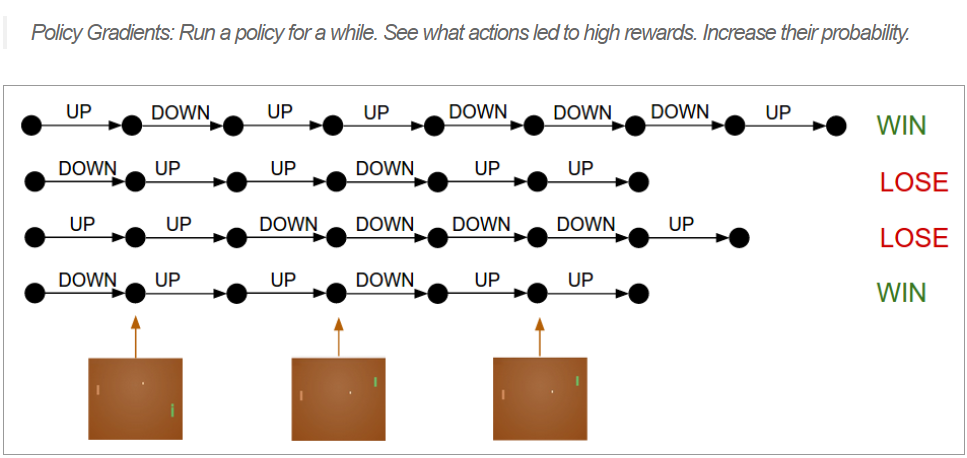
\[ R(s,a) \nabla \pi_{\theta_{t}}(a \mid s) \approx \nabla \pi_{\theta_{t}}(a^{*} \mid s) \]

最后，由于采样到的action分布服从于\(a \sim \pi_{\theta}(a)\) ，除掉 \(\pi_{\theta}\) ：

\(G_{t} \frac{\nabla \pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)}{\pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)}\)

此时，采样的均值可以去无偏估计2.2式中的Expectation。

\[ \sum_N G_{t} \frac{\nabla \pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)}{\pi\left(A_{t} \mid S_{t}, \boldsymbol{\theta}_{t}\right)} \]

\[ =\mathbb{E}_{\pi}\left[\sum_{a} q_{\pi}\left(S_{t}, a\right) \nabla \pi\left(a \mid S_{t}, \boldsymbol{\theta}\right)\right] \]