从这期开始我们进入Sutton强化学习第二版,第五章蒙特卡洛方法。蒙特卡洛方法是一种在工程各领域都存在的基本方法,在强化领域中,其特点是无需知道环境的dynamics,只需不断模拟记录并分析数据即可逼近理论真实值。蒙特卡洛方法本篇将会用21点游戏作为示例来具体讲解其原理和代码实现。
21点游戏问题
21点游戏是一个经典的赌博游戏。大致规则是玩家和庄家各发两张牌,一张明牌,一张暗牌。玩家和庄家可以决定加牌或停止加牌,新加的牌均为暗牌,最后比较两个玩家的牌面和,更接近21点的获胜。游戏的变化因素是牌Ace,既可以作为11也可以作为1来计算,算作11的时候称作usable。
Sutton教材中的21点游戏规则简化了几个方面用于控制问题状态数:
- 已发的牌的无状态性:和一副牌的21点游戏不同的是,游戏环境简化为牌是可以无穷尽被补充的,一副牌的某一张被派发后,同样的牌会被补充进来,或者可以认为每次发放的牌都是从一副新牌中抽出的。统计学中的术语称为重复采样(sample with replacement)。这种规则下极端情况下,玩家可以拥有 5个A或者5个2。另外,这会导致玩家无法通过开局看到的3张牌的信息推断后续发牌的概率,如此就大规模减小了游戏状态数。
- 庄家和玩家独立游戏,无需按轮次要牌。开局给定4张牌后,玩家先行动,加牌直至超21点或者停止要牌,如果超21点,玩家输,否则,等待庄家行动,庄家加牌直至超21点或者停止要牌,如果超21点,庄家输,否则比较两者的总点数。这种方式可以认为当玩家和庄家看到初始的三张牌后独立做一系列决策,最后比较结果,避免了交互模式下因为能观察到每一轮后对方牌数变化产生额外的信息而导致的游戏状态数爆炸。
有以上两个规则的简化,21点游戏问题的总状态数有下面三个维度
自己手中的点数和(12到21)
庄家明牌的点数(A到10)
庄家明牌是否有 A(True, False)。
状态总计总数为三个维度的乘积 10 * 10 * 2 = 200。
关于游戏状态有几个比较subtle的假设或者要素。首先,玩家初始时能看到三张牌,这三张牌确定了状态的三个维度的值,当然也就确定了Agent的初始状态,随后按照独立游戏的规则进行,玩家根据初始状态依照某种策略决策要牌还是结束要牌,新拿的牌更新了游戏状态,玩家转移到新状态下继续做决策。举个例子,假设初始时玩家明牌为8,暗牌为6,庄家明牌为7,则游戏状态为Tuple (14, 7, False)。若玩家的策略为教材中的固定规则策略:没到20或者21继续要牌。下一步玩家拿到牌3,则此时新状态为 (17, 7, False),按照策略继续要牌。
第二个方面是游戏的状态完全等价于玩家观察到的信息。比如尽管初始时有4张牌,真正的状态是这四张牌的值,但是出于简化目的,不考虑partially observable 的情况,即不将暗牌纳入游戏状态中。另外,庄家做决策的时候也无法得知玩家的手中的总牌数。
第三个方面是关于玩家点数。考虑玩家初始时的两张牌为2,3,总点数是5,那么为何不将5加入到游戏状态中呢?原则上是可以将初始总和为2到11都加入到游戏状态,但是意义不大,原因在于我们已经假设了已发牌的无状态性,拿到的这两张牌并不会改变后续补充的牌的出现概率。当玩家初始总和为2到11时一定会追加牌,因为无论第三张牌是什么,都不会超过21点,只会增加获胜概率。若后续第三张牌为8,总和变成13,就进入了有效的游戏状态,因为此时如果继续要牌,获得10,则游戏输掉。因此,我们关心的游戏状态并不完全等价于所有可能的游戏状态。
21点游戏 OpenAI Gym环境
OpenAI Gym 已经实现了Sutton版本的21点游戏环境,并按上述规则来进行。在安装完OpenAI Gym包之后 import BlackjackEnv即可使用。
1 | from gym.envs.toy_text import BlackjackEnv |
根据这个游戏环境,我们先来定义一些类型,可以令代码更具可读性和抽象化。State 上文说过是由三个分量组成的Tuple。Action 为bool类型 表示是否继续要牌。Reward 为+1或者-1,玩家叫牌过程中为0。StateValue 为书中的 \(V_{\pi}\),实现上是一个Dict。DeterministicPolicy 为一个函数,输入是某一状态,输出是唯一的决策动作。
1 | State = Tuple[int, int, bool] |
以下代码是 BlackjackEnv 核心代码,step 方法的输入为玩家的决策动作(叫牌还是结束),并输出State, Reward, is_done。简单解释一下代码逻辑,当玩家继续加牌时,需要判断是否超21点,如果没有超过的话,返回下一状态,同时reward 为0,等待下一step方法。若玩家停止叫牌,则按照庄家策略:小于17时叫牌。游戏终局时产生+1表示玩家获胜,-1表示庄家获胜。
1 | class BlackjackEnv(gym.Env): |
下面示例如何调用step方法生成一个episode的数据集。数据集的类型为 List[Tuple[State, Action, Reward]]。
1 | def gen_episode_data(policy: DeterministicPolicy, env: BlackjackEnv) -> List[Tuple[State, Action, Reward]]: |
策略的蒙特卡洛值预测
Monte Carlo Prediction解决如下问题:当给定Agent 策略\(\pi\)时,反复试验来预估策略的 \(V_{\pi}\) 值。具体来说,产生一系列的episode数据之后,对于出现了的所有状态分别计算其Return,再通过 average 某一状态 s 的Return来估计 \(V_{\pi}(s)\),理论上,依据大数定理(Law of large numbers),在可以无限模拟的情况下,Monte Carlo prediction 一定会收敛到真实的 \(V_{\pi}\)。算法实现上有两个略微不同的版本,一个版本称为 First-visit,另一个版本称为 Every-visit,区别在于如何计算出现的状态 s 的 Return值。
对于 First-visit 来说,当状态 s 第一次出现时计算一次 Returns,若继续出现状态 s 不再重复计算。对于Every-visit来说,每次出现 s 计算一次 Returns(s)。举个例子,某episode 数据如下: \[ S_1, R_1, S_2, R_2, S_1, R_3, S_3, R_4 \] First-visit 对于状态S1的Returns计算为
\[ Returns(S_1) = R_1 + R_2 + R_3 + R_4 \]
Every-visit 对于状态S1的Returns计算了两次,因为S1出现了两次。 \[ \begin{align*} Returns(S_1) = \frac{Return_1(S_1) + Return_2(S_1)}2 \\ = \frac{(R_1 + R_2 + R_3 + R_4) + (R_3 + R_4)} 2 \end{align*} \]
下面用Monte Carlo来模拟解得书中示例玩家固定策略的V值,策略具体为:加牌直到手中点数>=20,代码为
1 | def fixed_policy(observation): |
First-visit MC Predicition
伪代码如下,注意考虑到实现上的高效性,在遍历episode序列数据时是从后向前扫的,这样可以边扫边更新G。\[ \begin{align*} &\textbf{First-visit MC prediction, for estimating } V \approx v_{\pi} \\ & \text{Input: a policy } \pi \text{ to be evaluated} \\ & \text{Initialize} \\ & \quad V(s) \in \mathbb R \text{, arbitrarily, for all }s \in \mathcal{S} \\ & \quad Returns(s) \leftarrow \text{ an empty list, arbitrarily, for all }s \in \mathcal{S} \\ & \\ & \text{Loop forever (for episode):}\\ & \quad \text{Generate an episode following } \pi: S_0, A_0, R_1, S_1, A_1, R_2, ..., S_{T-1}, A_{T-1}, R_T\\ & \quad G \leftarrow 0\\ & \quad \text{Loop for each step of episode, } t = T-1, T-2, ..., 0:\\ & \quad \quad \quad G \leftarrow \gamma G + R_{t+1}\\ & \quad \quad \quad \text{Unless } S_t \text{ appears in } S_0, S_1, ..., S_{t-1}\\ & \quad \quad \quad \quad \text{Append } G \text { to }Returns(S_t) \\ & \quad \quad \quad \quad V(S_t) \leftarrow \operatorname{average}(Returns(S_t))\\ \end{align*} \]
对应的 python 实现
1 | def mc_prediction_first_visit(policy: DeterministicPolicy, env: BlackjackEnv, |
Every-visit MC Prediciton
Every-visit 代码实现相对更简单一些,t 从后往前遍历时更新对应s的状态变量。如下所示
1 | def mc_prediction_every_visit(policy: DeterministicPolicy, env: BlackjackEnv, |
策略 V值 3D 可视化
运行first-visit 算法,模拟10000次episode,fixed_policy的V值的3D图为下面两张图,分别是不含usable Ace和包含usable Ace。总的说来,一旦玩家能到达20点或21点获胜概率极大,到达13-17获胜概率较小,在11-13时有一定获胜概率,比较符合经验直觉。
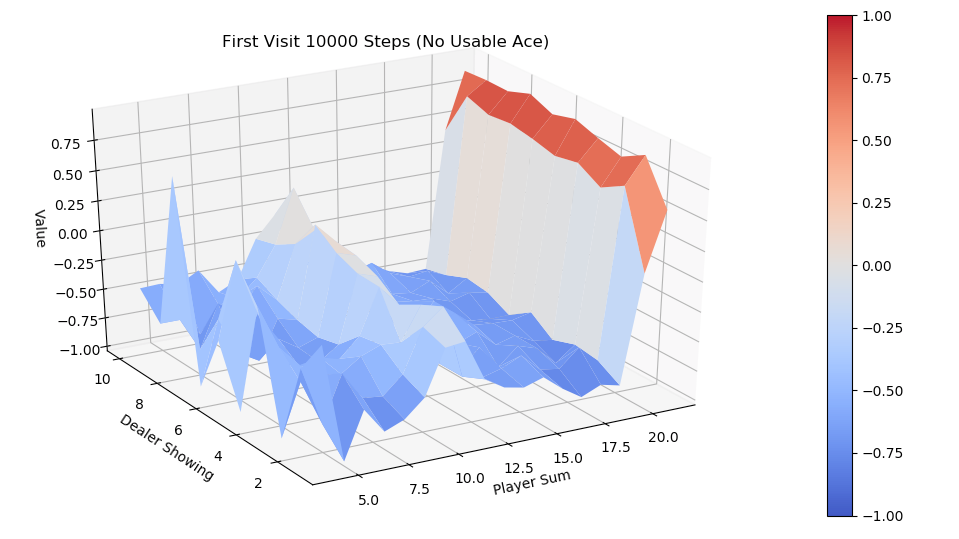
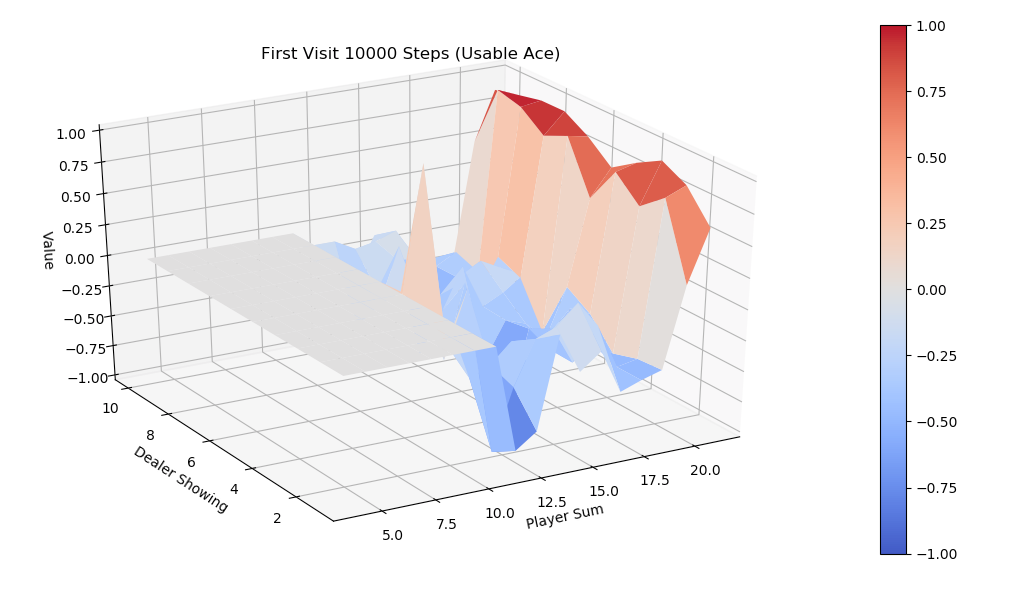
同样运行every-visit 算法,模拟10000次的V值图。对比两种方法结果比较接近。
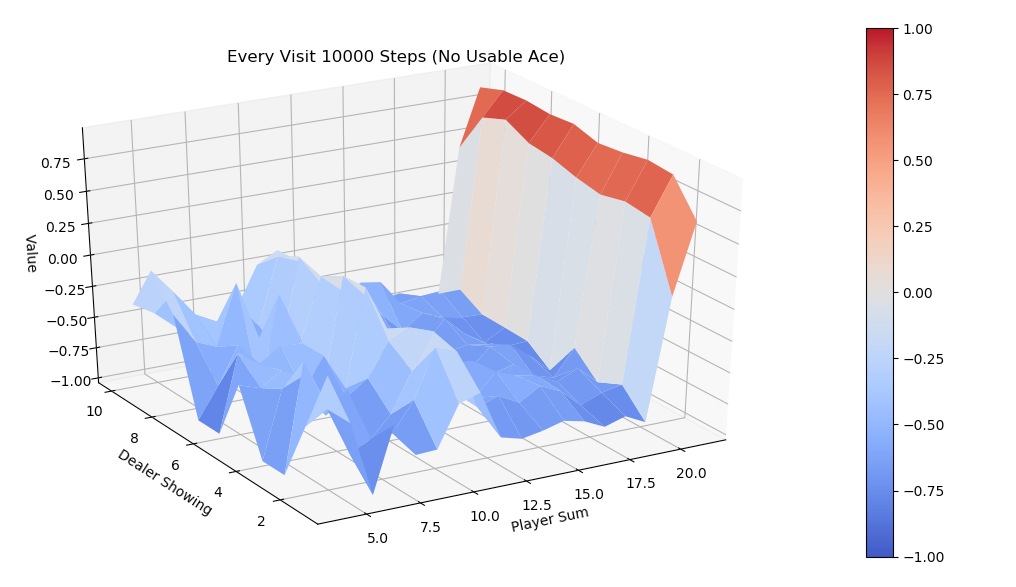
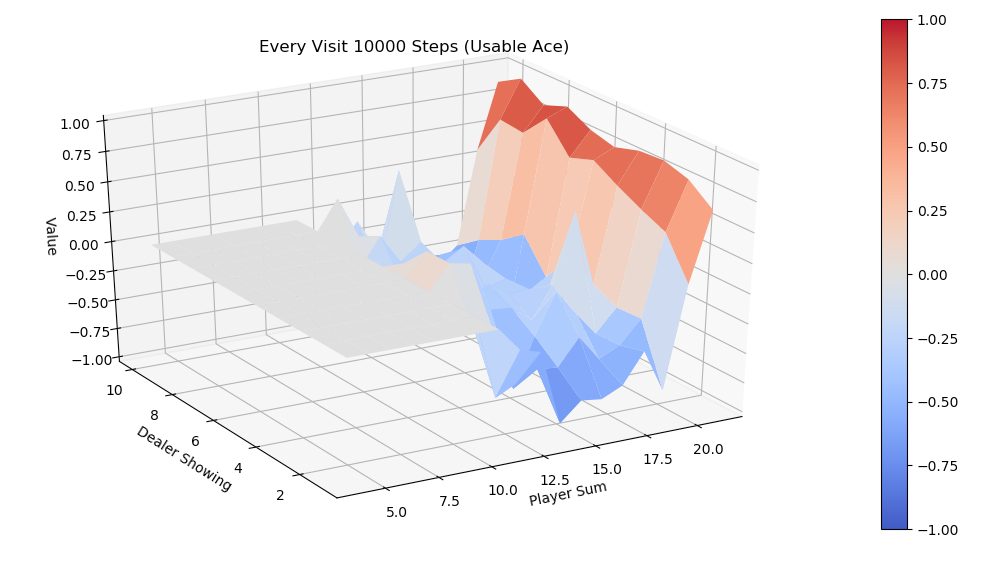

评论
shortnamefor Disqus. Please set it in_config.yml.