通过代码学Sutton强化学习4：21点游戏的蒙特卡洛On-Policy控制

这期继续Sutton强化学习第二版，第五章蒙特卡洛方法。在上期21点游戏的策略蒙特卡洛值预测学习了如何用Monte Carlo来预估给定策略 \(\pi\) 的 \(V_{\pi}\) 值之后，这一期我们用Monte Carlo方法来解得21点游戏最佳策略 \(\pi_{*}\)。

蒙特卡洛策略提升

回顾一下，在Grid World 策略迭代和值迭代中由于存在Policy Improvement Theorem，我们可以利用环境dynamics信息计算出策略v值，再选取最greedy action的方式改进策略，形成策略提示最终能够不断逼近最佳策略。 \[ \pi_{0} \stackrel{\mathrm{E}}{\longrightarrow} v_{\pi_{0}} \stackrel{\mathrm{I}}{\longrightarrow} \pi_{1} \stackrel{\mathrm{E}}{\longrightarrow} v_{\pi_{1}} \stackrel{\mathrm{I}}{\longrightarrow} \pi_{2} \stackrel{\mathrm{E}}{\longrightarrow} \cdots \stackrel{\mathrm{I}}{\longrightarrow} \pi_{*} \stackrel{\mathrm{E}}{\longrightarrow} v_{*} \] Monte Carlo Control方法搜寻最佳策略 \(\pi{*}\)，是否也能沿用同样的思路呢？答案是可行的。不过，不同于第四章中我们已知环境MDP就知道状态的前后依赖关系，进而从v值中能推断出策略 \(\pi\)，在Monte Carlo方法中，环境MDP是未知的，因而我们只能从action-value中下手，通过海量Monte Carlo试验来近似 \(q_{\pi}\)。有了策略 Q 值，再和MDP策略迭代方法一样，选取最greedy action的策略，这种策略提示方式理论上被证明了最终能够不断逼近最佳策略。 \[ \pi_{0} \stackrel{\mathrm{E}}{\longrightarrow} q_{\pi_{0}} \stackrel{\mathrm{I}}{\longrightarrow} \pi_{1} \stackrel{\mathrm{E}}{\longrightarrow} q_{\pi_{1}} \stackrel{\mathrm{I}}{\longrightarrow} \pi_{2} \stackrel{\mathrm{E}}{\longrightarrow} \cdots \stackrel{\mathrm{I}}{\longrightarrow} \pi_{*} \stackrel{\mathrm{E}}{\longrightarrow} q_{*} \]

但是此方法有一个前提要满足，由于数据是依据策略 \(\pi_{i}\) 生成的，理论上需要保证在无限次的模拟过程中，每个状态都必须被无限次访问到，才能保证最终每个状态的Q估值收敛到真实的 \(q_{*}\)。满足这个前提的一个简单实现是强制随机环境初始状态，保证每个状态都能有一定概率被生成。这个思路就是 Monte Carlo Control with Exploring Starts算法，伪代码如下：

\[ \begin{align*} &\textbf{Monte Carlo ES (Exploring Starts), for estimating } \pi \approx \pi_{*} \\ & \text{Initialize:} \\ & \quad \pi(s) \in \mathcal A(s) \text{ arbitrarily for all }s \in \mathcal{S} \\ & \quad Q(s, a) \in \mathbb R \text{, arbitrarily, for all }s \in \mathcal{S}, a \in \mathcal A(s) \\ & \quad Returns(s, a) \leftarrow \text{ an empty list, for all }s \in \mathcal{S}, a \in \mathcal A(s)\\ & \\ & \text{Loop forever (for episode):}\\ & \quad \text{Choose } S_0\in \mathcal{S}, A_0 \in \mathcal A(S_0) \text{ randomly such that all pairs have probability > 0} \\ & \quad \text{Generate an episode from } S_0, A_0 \text{, following } \pi : S_0, A_0, R_1, S_1, A_1, R_2, ..., S_{T-1}, A_{T-1}, R_T\\ & \quad G \leftarrow 0\\ & \quad \text{Loop for each step of episode, } t = T-1, T-2, ..., 0:\\ & \quad \quad \quad G \leftarrow \gamma G + R_{t+1}\\ & \quad \quad \quad \text{Unless the pair } S_t, A_t \text{ appears in } S_0, A_0, S_1, A_1, ..., S_{t-1}, A_{t-1}\\ & \quad \quad \quad \quad \text{Append } G \text { to }Returns(S_t, A_t) \\ & \quad \quad \quad \quad Q(S_t, A_t) \leftarrow \operatorname{average}(Returns(S_t, A_t))\\ & \quad \quad \quad \quad \pi(S_t) \leftarrow \operatorname{argmax}_a Q(S_t, a)\\ \end{align*} \]

下面我们实现21点游戏的Monte Carlo ES 算法。21点游戏只有200个有效的状态，可以满足算法要求的生成episode前先随机选择某一状态的前提条件。

相对于上一篇，我们增加 ActionValue和Policy的类型定义，ActionValue表示 \(q(s, a)\) ，是一个State到动作分布的Dict，Policy 类型也一样。Actions为一维ndarray，维数是离散动作数量。

{linenos

State = Tuple[int, int, bool]
Action = bool
Reward = float
Actions = np.ndarray
ActionValue = Dict[State, Actions]
Policy = Dict[State, Actions]

下面代码示例如何给定 Policy后，依据指定状态state的动作分布采样，决定下一动作。

policy: Policy
A: ActionValue = policy[state]
action = np.random.choice([0, 1], p=A/sum(A))

整个算法的 python 代码实现如下：

{linenos

def mc_control_exploring_starts(env: BlackjackEnv, num_episodes, discount_factor=1.0) \
        -> Tuple[ActionValue, Policy]:
    states = list(product(range(10, 22), range(1, 11), (True, False)))
    policy = {s: np.ones(env.action_space.n) * 1.0 / env.action_space.n for s in states}
    Q = defaultdict(lambda: np.zeros(env.action_space.n))
    returns_sum = defaultdict(float)
    returns_count = defaultdict(float)

    for episode_i in range(1, num_episodes + 1):
        s0 = random.choice(states)
        reset_env_with_s0(env, s0)
        episode_history = gen_custom_s0_stochastic_episode(policy, env, s0)

        G = 0
        for t in range(len(episode_history) - 1, -1, -1):
            s, a, r = episode_history[t]
            G = discount_factor * G + r
            if not any(s_a_r[0] == s and s_a_r[1] == a for s_a_r in episode_history[0: t]):
                returns_sum[s, a] += G
                returns_count[s, a] += 1.0
                Q[s][a] = returns_sum[s, a] / returns_count[s, a]
                best_a = np.argmax(Q[s])
                policy[s][best_a] = 1.0
                policy[s][1-best_a] = 0.0

    return Q, policy

在MC Exploring Starts 算法中，我们需要指定环境初始状态，一种做法是env.reset()时接受初始状态，但是考虑到不去修改第三方实现的 BlackjackEnv类，采用一个取巧的办法，在调用reset()后直接改写env 的私有变量，这个逻辑封装在 reset_env_with_s0 方法中。

{linenos

def reset_env_with_s0(env: BlackjackEnv, s0: State) -> BlackjackEnv:
    env.reset()
    player_sum = s0[0]
    oppo_sum = s0[1]
    has_usable = s0[2]

    env.dealer[0] = oppo_sum
    if has_usable:
        env.player[0] = 1
        env.player[1] = player_sum - 11
    else:
        if player_sum > 11:
            env.player[0] = 10
            env.player[1] = player_sum - 10
        else:
            env.player[0] = 2
            env.player[1] = player_sum - 2
    return env

算法结果的可视化和理论对比

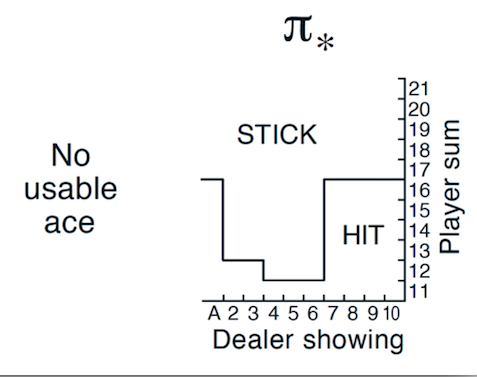
下图是有Usable Ace情况下的理论最优策略。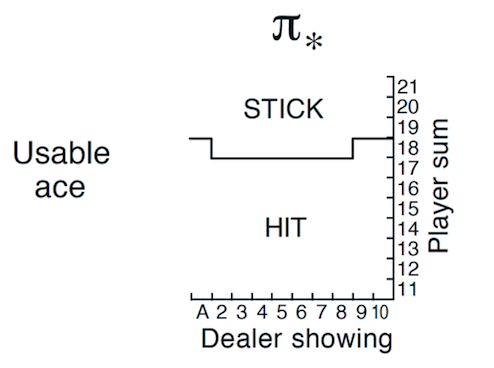

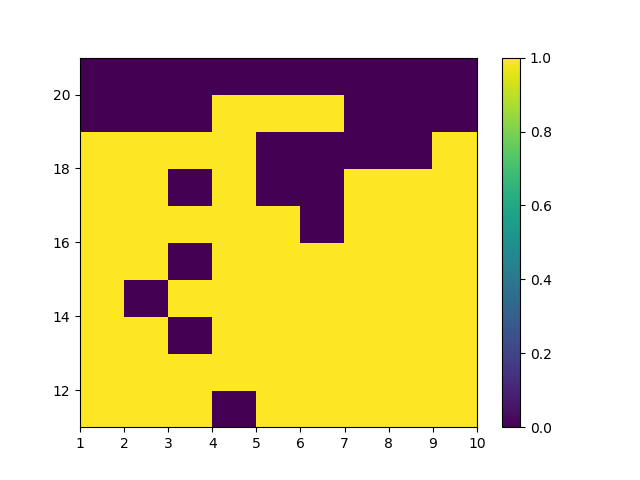
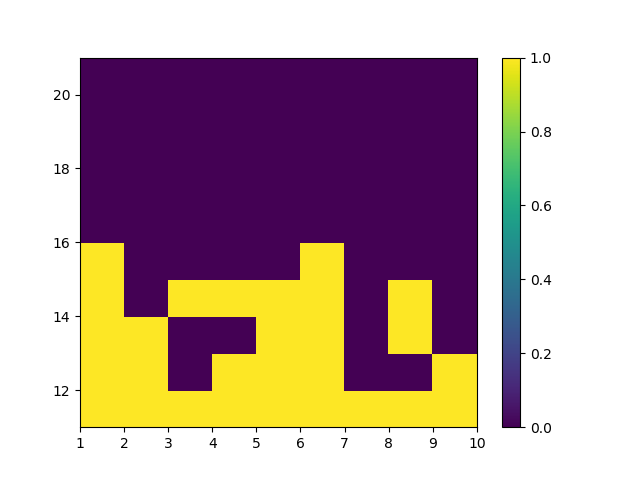
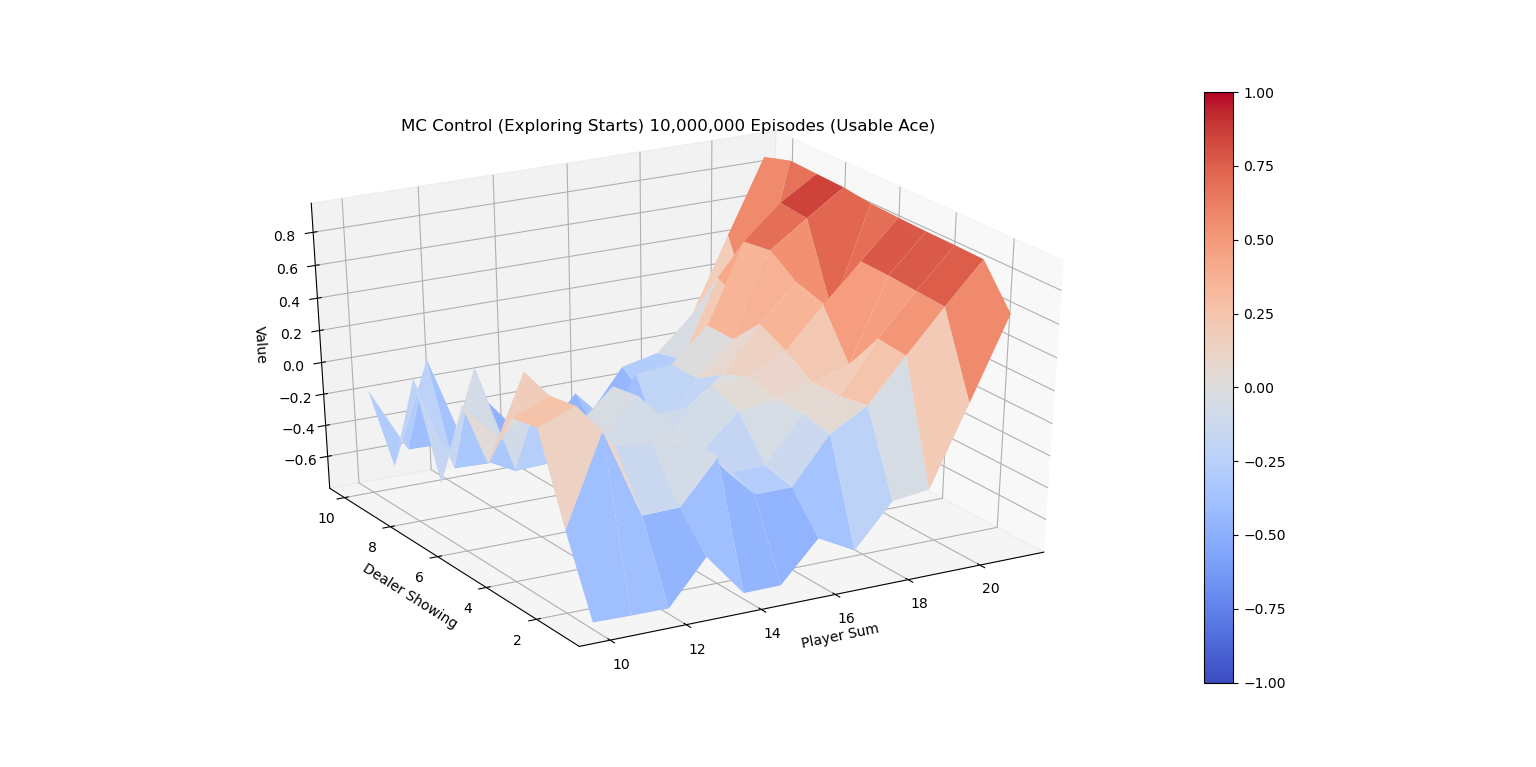
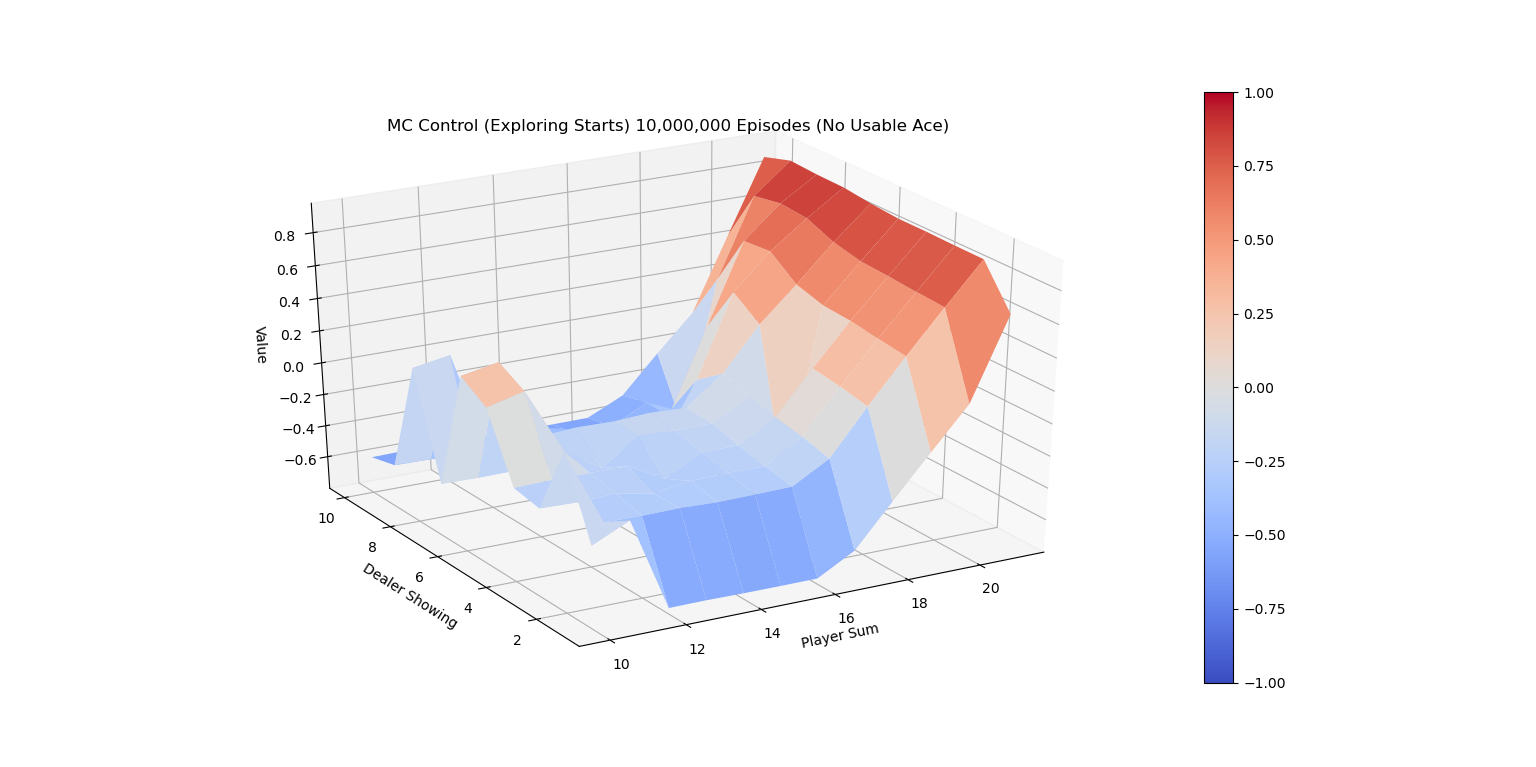
理论最佳策略（有Ace）

Monte Carlo方法策略提示的收敛是比较慢的，下图是运行10,000,000次episode后有Usable Ace时的策略 \(\pi_{*}^{\prime}\)。对比理论最优策略，MC ES在不少的状态下还未收敛到理论最优解。

MC ES 10M的最佳策略（有Ace）

同样的，下两张图是无Usable Ace情况下的理论最优策略和试验结果的对比。

理论最佳策略（无Ace）

MC ES 10M的最佳策略（无Ace）

下面的两张图画出了运行代码10,000,000次episode后 \(\pi{*}\)的V值图。

MC ES 10M的最佳V值（有Ace）

MC ES 10M的最佳V值（无Ace）

Exploring Starts 蒙特卡洛控制改进

为了避免Monte Carlo ES Control在初始时必须访问到任意状态的限制，教材中介绍了一种改进算法，On-policy first-visit MC control for \(\epsilon \text{-soft policies}\) ，它同样基于Monte Carlo 预估Q值，但用 \(\epsilon \text{-soft}\) 策略来代替最有可能的action策略作为下一次迭代策略，\(\epsilon \text{-soft}\) 本质上来说就是对于任意动作都保留 \(\epsilon\) 小概率的访问可能，权衡了exploration和exploitation，由于每个动作都可能被无限次访问到，Explorting Starts中的强制随机初始状态就可以去除了。Monte Carlo ES Control 和 On-policy first-visit MC control for \(\epsilon \text{-soft policies}\) 都属于on-policy算法，其区别于off-policy的本质在于预估 \(q_{\pi}(s,a)\)时是否从同策略\(\pi\)生成的数据来计算。一个比较subtle的例子是著名的Q-Learning，因为根据这个定义，Q-Learning属于off-policy。

\[ \begin{align*} &\textbf{On-policy first-visit MC control (for }\epsilon \textbf{-soft policies), estimating } \pi \approx \pi_{*} \\ & \text{Algorithm parameter: small } \epsilon > 0 \\ & \text{Initialize:} \\ & \quad \pi \leftarrow \text{ an arbitrary } \epsilon \text{-soft policy} \\ & \quad Q(s, a) \in \mathbb R \text{, arbitrarily, for all }s \in \mathcal{S}, a \in \mathcal A(s) \\ & \quad Returns(s, a) \leftarrow \text{ an empty list, for all }s \in \mathcal{S}, a \in \mathcal A(s)\\ & \\ & \text{Repeat forever (for episode):}\\ & \quad \text{Generate an episode following } \pi : S_0, A_0, R_1, S_1, A_1, R_2, ..., S_{T-1}, A_{T-1}, R_T\\ & \quad G \leftarrow 0\\ & \quad \text{Loop for each step of episode, } t = T-1, T-2, ..., 0:\\ & \quad \quad \quad G \leftarrow \gamma G + R_{t+1}\\ & \quad \quad \quad \text{Unless the pair } S_t, A_t \text{ appears in } S_0, A_0, S_1, A_1, ..., S_{t-1}, A_{t-1}\\ & \quad \quad \quad \quad \text{Append } G \text { to }Returns(S_t, A_t) \\ & \quad \quad \quad \quad Q(S_t, A_t) \leftarrow \operatorname{average}(Returns(S_t, A_t))\\ & \quad \quad \quad \quad A^{*} \leftarrow \operatorname{argmax}_a Q(S_t, a)\\ & \quad \quad \quad \quad \text{For all } a \in \mathcal A(S_t):\\ & \quad \quad \quad \quad \quad \pi(a|S_t) \leftarrow \begin{cases} 1 - \epsilon + \epsilon / |\mathcal A(S_t)| & \text{ if } a = A^{*}\\ \epsilon / |\mathcal A(S_t)| & \text{ if } a \neq A^{*}\\ \end{cases} \\ \end{align*} \]

伪代码对应的 Python 实现如下。

{linenos

def mc_control_epsilon_greedy(env: BlackjackEnv, num_episodes, discount_factor=1.0, epsilon=0.1) \
        -> Tuple[ActionValue, Policy]:
    returns_sum = defaultdict(float)
    returns_count = defaultdict(float)

    states = list(product(range(10, 22), range(1, 11), (True, False)))
    policy = {s: np.ones(env.action_space.n) * 1.0 / env.action_space.n for s in states}
    Q = defaultdict(lambda: np.zeros(env.action_space.n))

    def update_epsilon_greedy_policy(policy: Policy, Q: ActionValue, s: State):
        policy[s] = np.ones(env.action_space.n, dtype=float) * epsilon / env.action_space.n
        best_action = np.argmax(Q[s])
        policy[s][best_action] += (1.0 - epsilon)

    for episode_i in range(1, num_episodes + 1):
        episode_history = gen_stochastic_episode(policy, env)

        G = 0
        for t in range(len(episode_history) - 1, -1, -1):
            s, a, r = episode_history[t]
            G = discount_factor * G + r
            if not any(s_a_r[0] == s and s_a_r[1] == a for s_a_r in episode_history[0: t]):
                returns_sum[s, a] += G
                returns_count[s, a] += 1.0
                Q[s][a] = returns_sum[s, a] / returns_count[s, a]
                update_epsilon_greedy_policy(policy, Q, s)

    return Q, policy