通过代码学Sutton强化学习1：Grid World OpenAI环境和策略评价算法

经典教材Reinforcement Learning: An Introduction 第二版由强化领域权威Richard S. Sutton 和 Andrew G. Barto 完成编写，内容深入浅出，非常适合初学者。在本篇中，引入Grid World示例，结合强化学习核心概念，并用python代码实现OpenAI Gym的模拟环境，进一步实现策略评价算法。

Grid World 问题

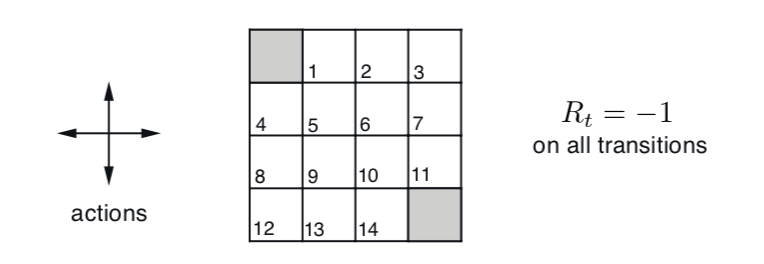
第四章例子4.1提出了一个简单的离散空间状态问题：Grid World，其大致意思是在4x4的网格世界中有14个格子是非终点状态，在这些非终点状态的格子中可以往上下左右四个方向走，直至走到两个终点状态格子，则游戏结束。每走一步，Agent收获reward -1，表示Agent希望在Grid World中尽早出去。另外，Agent在Grid World边缘时，无法继续往外只能呆在原地，reward也是-1。

Finite MDP 模型

先来回顾一下强化学习的建模基础：有限马尔可夫决策过程（Finite Markov Decision Process, Finite MDP）。如下图，强化学习模型将世界抽象成两个实体，强化学习解决目标的主体Agent和其他外部环境。它们之间的交互过程遵从有限马尔可夫决策过程：若Agent在t时间步骤时处于状态 \(S_t\)，采取动作 \(A_t\)，然后环境根据自身机制，产生Reward \(R_{t+1}\) 并将Agent状态变为 \(S_{t+1}\)。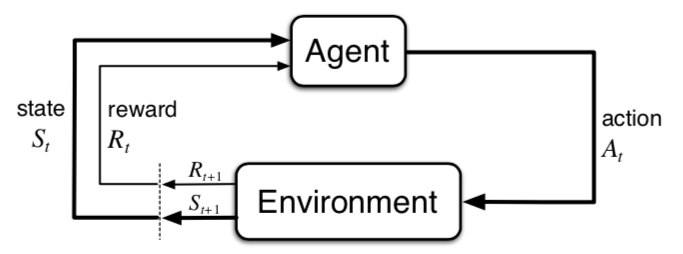

环境自身机制又称为dynamics，工程上可以看成一个输入(S, A)，输出(S, R)的方法。由于MDP包含随机过程，某个输入并不能确定唯一输出，而会根据概率分布输出不同的(S, R)。Finite MDP简化了时间对于模型的影响，因为(S, R)只和(S, A)有关，不和时间t有关。另外，有限指的是S，A，R的状态数量是有限的。

数学上dynamics可以如下表示

\[ p\left(s^{\prime}, r \mid s, a\right) \doteq \operatorname{Pr}\left\{S_{t}=s^{\prime}, R_{t}=r \mid S_{t-1}=s, A_{t-1}=a\right\} \]

即是四元组作为输入的概率函数 \(p: S \times R \times S \times A \rightarrow [0, 1]\)。

满足 \[ \sum_{s^{\prime} \in \mathcal{S}} \sum_{r \in \mathcal{R}} p\left(s^{\prime}, r \mid s, a\right)=1, \text { for all } s \in \mathcal{S}, a \in \mathcal{A}(s) \]

以Grid World为例，当Agent处于编号1的网格时，可以往四个方向走，往任意方向走都只产生一种 S, R，因为这个简单的游戏是确定性的，不存在某一动作导致stochastic状态。例如，在1号网格往左就到了终点网格（编号0），得到Reward -1这个规则可以如下表示 \[ p\left(s^{\prime}=0, r=-1 \mid s=1, a=\text{L}\right) = 1 \] 因此，状态s=1的所有dynamics概率映射为

\[ \begin{aligned} p\left(s^{\prime}=0, r=-1 \mid s=1, a=\text{L}\right) &=& 1 \\ p\left(s^{\prime}=2, r=-1 \mid s=1, a=\text{R}\right) &=& 1 \\ p\left(s^{\prime}=1, r=-1 \mid s=1, a=\text{U}\right) &=& 1 \\ p\left(s^{\prime}=5, r=-1 \mid s=1, a=\text{D}\right) &=& 1 \end{aligned} \]

强化学习的目的

在给定了问题以及定义了强化学习的模型之后，强化学习的目的当然是通过学习让Agent能够学到最佳策略\(\pi_{*}\)，也就是在某个状态下的行动分布，记成 \(\pi(a|s)\)。对应在数值上的优化目标是Agent在一系列过程中采取某种策略的reward总和的期望（Expected Return）。下面公式定义了t步往后的reward总和，其中 \(\gamma\) 为discount factor，用于权衡短期和长期reward对于当前Agent的效用影响。等式最后一步的意义是t步后的reward总和等价于t步所获的立即reward \(R_{t+1}\)，加上t+1步后的reward总和 \(\gamma G_{t+1}\)。

\[ \begin{aligned} G_{t} & \doteq R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\gamma^{3} R_{t+4}+\cdots \\ &=R_{t+1}+\gamma\left(R_{t+2}+\gamma R_{t+3}+\gamma^{2} R_{t+4}+\cdots\right) \\ &=R_{t+1}+\gamma G_{t+1} \end{aligned} \]

有了reward总和的定义，评价Agent策略 \(\pi\) 就可以定义成Agent在状态 s 时采用此策略的Expected Return。

\[ v_{\pi}(s) \doteq \mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s\right] \]

下面公式推导了 \(v_{\pi}(s)\) 数值上和相关状态 \(s{\prime}\) 的关系：

\[ \begin{aligned} v_{\pi}(s) &\doteq \mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s\right] \\ &=\mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \mid S_{t}=s\right]\\ &=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma G_{t+1} \mid S_{t}=s\right] \\ &=\sum_{a} \pi(a \mid s) \sum_{s^{\prime}} \sum_{r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma \mathbb{E}_{\pi}\left[G_{t+1} \mid S_{t+1}=s^{\prime}\right]\right] \\ &=\sum_{a} \pi(a \mid s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\pi}\left(s^{\prime}\right)\right] \quad \text { for all } s \in \mathcal{S} \end{aligned} \]

注意到如果将 \(v_{\pi}(s)\) 看成未知数，上式即形成 \(\mid \mathcal{S} \mid\) 个未知变量的方程组，可以在数值上解得各个 \(v_{\pi}(s)\)。

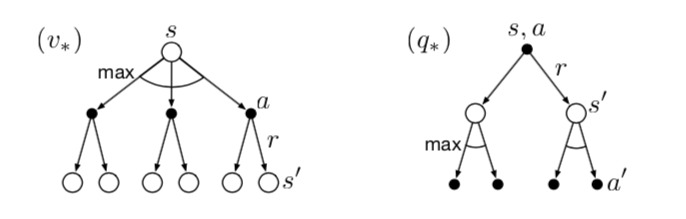
书中用Backup Diagram来表示递推关系，下图是\(v_{\pi}(s)\)的backup diagram。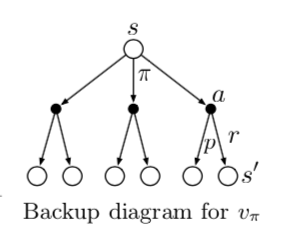

尽管v值可以来衡量策略，但由于\(v_{\pi}(s)\) 是Agent在策略\(\pi(a|s)\)的Expected Return，将不同的action拆出来单独计算Expected Return，这样的做法有时更为直接，这就是著名的Q Learning中的q 值，记成\(q_{\pi}(s, a)\) 。

\[ q_{\pi}(s, a) \doteq \mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s, A_{t}=a\right] \]

下面是 $q_{}(s, a) $ 的递推 backup diagram。

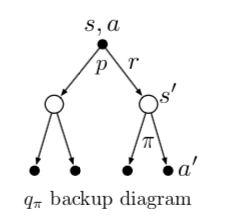
Bellman 最佳原则

对于所有状态集合\(\mathcal{S}\)，策略\({\pi}\)的评价指标 \(v_{\pi}(s)\) 是一个向量，本质上是无法相互比较的。但由于存在Bellman 最佳原则（Bellman's principle of optimality）：在有限状态情况下，一定存在一个或者多个最好的策略 \({\pi}_{*}\)，它在所有状态下的v值都是最好的，即 \(v_{\pi_{*}}(s) \ge v_{\pi^{\prime}}(s) \text { for all } s \in \mathcal{S}\)。

因此，最佳v值定义为最佳策略 \({\pi}_{*}\) 对应的 v 值

\[ v_{*}(s) \doteq \max_{\pi} v_{\pi}(s) \]

同理，也存在最佳q值，记为 \[ \begin{aligned} q_{*}(s, a) &\doteq \max_{\pi} q_{\pi}(s,a) \end{aligned} \]

将 \(v_{*}(s)\) 改写成递推形式，称为 Bellman Optimality Equation，推导如下

\[ \begin{aligned} v_{*}(s) &=\max _{a \in \mathcal{A}(s)} q_{\pi_{*}}(s, a) \\ &=\max _{a} \mathbb{E}_{\pi_{*}}\left[G_{t} \mid S_{t}=s, A_{t}=a\right] \\ &=\max _{a} \mathbb{E}_{\pi_{*}}\left[R_{t+1}+\gamma G_{t+1} \mid S_{t}=s, A_{t}=a\right] \\ &=\max _{a} \mathbb{E}\left[R_{t+1}+\gamma v_{*}\left(S_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] \\ &=\max _{a} \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{*}\left(s^{\prime}\right)\right] \end{aligned} \]

直觉上可以理解为状态 s 对应的最佳v值是只采取此状态下的最佳动作后的Expected Return。

最佳q值递归形式的意义为最佳策略下状态s时采取行动 a 的Expected Return，等于所有可能后续状态 s' 下采取最优行动的Expected Return的均值。推导如下：

\[ \begin{aligned} q_{*}(s, a) &=\mathbb{E}\left[R_{t+1}+\gamma \max _{a^{\prime}} q_{*}\left(S_{t+1}, a^{\prime}\right) \mid S_{t}=s, A_{t}=a\right] \\ &=\sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma \max _{a^{\prime}} q_{*}\left(s^{\prime}, a^{\prime}\right)\right] \end{aligned} \]

\(v_{*}(s), q_{*}(s, a)\) 的backup diagram 如下图

Grid World 最佳策略和V值

Grid World 的最佳策略如下：尽可能快的走出去

Grid World最佳策略

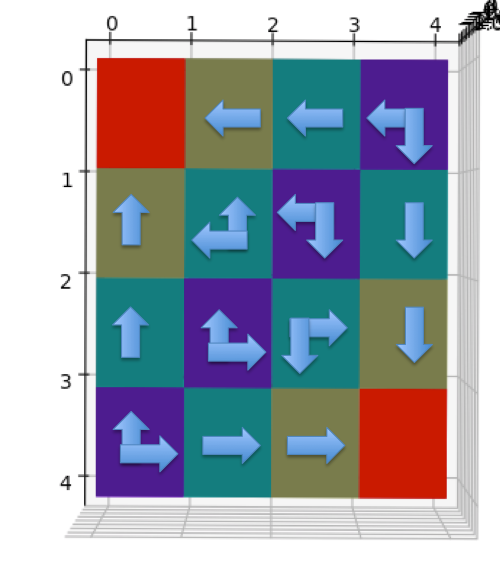
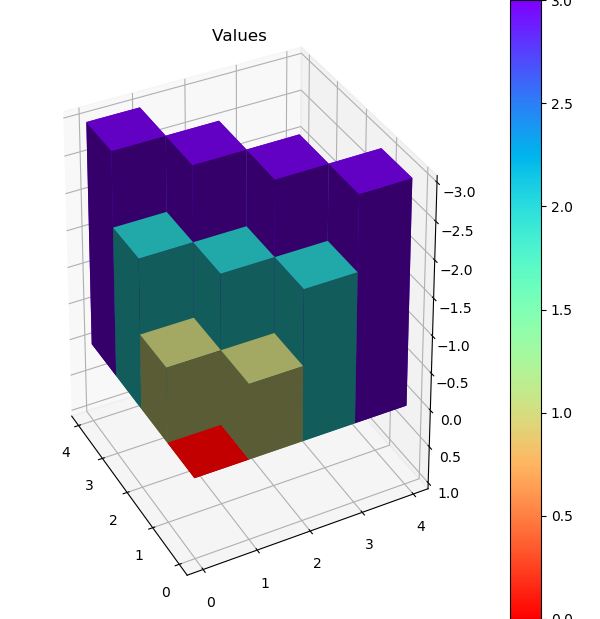
上面的2D图中不同颜色表示不同V值，终点格子的红色表示0，隔着一步的黄色为-1，隔两步的绿色为-2，最远的紫色为-3。下面是立体图示。

Grid World最佳策略V值

Grid World OpenAI Gym 环境

下面是OpenAI Gym框架下Grid World环境的代码实现。本质是在GridWorldEnv构造函数中构建MDP，类型定义如下

MDP = Dict[State, Dict[Action, List[Tuple[Prob, State, Reward, bool]]]]

# P[state][action] = [
#    (prob1, next_state1, reward1, is_done),
#    (prob2, next_state2, reward2, is_done), ...]

{linenos

class Action(Enum):
    UP = 0
    DOWN = 1
    LEFT = 2
    RIGHT = 3

State = int
Reward = float
Prob = float
Policy = Dict[State, Dict[Action, Prob]]
Value = List[float]
StateSet = Set[int]
NonTerminalStateSet = Set[int]
MDP = Dict[State, Dict[Action, List[Tuple[Prob, State, Reward, bool]]]]
# P[s][a] = [(prob, next_state, reward, is_done), ...]

class GridWorldEnv(discrete.DiscreteEnv):
    """
    Grid World environment described in Sutton and Barto Reinforcement Learning 2nd, chapter 4.
    """

    def __init__(self, shape=[4,4]):
        self.shape = shape
        nS = np.prod(shape)
        nA = len(list(Action))
        MAX_R = shape[0]
        MAX_C = shape[1]
        self.grid = np.arange(nS).reshape(shape)
        isd = np.ones(nS) / nS

        # P[s][a] = [(prob, next_state, reward, is_done), ...]
        P: MDP = {}
        action_delta = {Action.UP: (-1, 0), Action.DOWN: (1, 0), Action.LEFT: (0, -1), Action.RIGHT: (0, 1)}
        for s in range(0, MAX_R * MAX_C):
            P[s] = {a.value : [] for a in list(Action)}
            is_terminal = self.is_terminal(s)
            if is_terminal:
                for a in list(Action):
                    P[s][a.value] = [(1.0, s, 0, True)]
            else:
                r = s // MAX_R
                c = s % MAX_R
                for a in list(Action):
                    neighbor_r = min(MAX_R-1, max(0, r + action_delta[a][0]))
                    neighbor_c = min(MAX_C-1, max(0, c + action_delta[a][1]))
                    s_ = neighbor_r * MAX_R + neighbor_c
                    P[s][a.value] = [(1.0, s_, -1, False)]

        super(GridWorldEnv, self).__init__(nS, nA, P, isd)

策略评估（Policy Evaluation）

策略评估需要解决在给定环境dynamics和Agent策略 \(\pi\)下，计算策略的v值 \(v_{\pi}\)。由于所有数量关系都已知，可以通过解方程组的方式求得，但通常会通过数值迭代的方式来计算，即通过一系列 \(v_{0}, v_{1}, ..., v_{k}\) 收敛至 \(v_{\pi}\)。如下迭代方式已经得到证明，当 \(k \rightarrow \infty\) 一定收敛至 \(v_{\pi}\)。

\[ \begin{aligned} v_{k+1}(s) & \doteq \mathbb{E}_{\pi}\left[R_{t+1}+\gamma v_{k}\left(S_{t+1}\right) \mid S_{t}=s\right] \\ &=\sum_{a} \pi(a \mid s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{k}\left(s^{\prime}\right)\right] \end{aligned} \]

书中具体伪代码如下

\[ \begin{align*} &\textbf{Iterative Policy Evaluation, for estimating } V\approx v_{\pi} \\ & \text{Input } {\pi}, \text{the policy to be evaluated} \\ & \text{Algorithm parameter: a small threshold } \theta > 0 \text{ determining accuracy of estimation} \\ & \text{Initialize } V(s), \text{for all } s \in \mathcal{S}^{+} \text{, arbitrarily except that } V (terminal) = 0\\ & \\ &1: \text{Loop:}\\ &2: \quad \quad \Delta \leftarrow 0\\ &3: \quad \quad \text{Loop for each } s \in \mathcal{S}:\\ &4: \quad \quad \quad \quad v \leftarrow V(s) \\ &5: \quad \quad \quad \quad V(s) \leftarrow \sum_{a} \pi(a \mid s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma V\left(s^{\prime}\right)\right] \\ &6: \quad \quad \quad \quad \Delta \leftarrow \max(\Delta, |v-V(s)|) \\ &7: \text{until } \Delta < \theta \end{align*} \]

下面是python 代码实现，注意这里单run迭代时，新的v值直接覆盖数组里的旧v值，这种做法在书中被证明不仅有效，甚至更为高效。这种做法称为原地（in place）更新。

{linenos

def policy_evaluate(policy: Policy, env: GridWorldEnv, gamma=1.0, theta=0.0001):
    V = np.zeros(env.nS)
    while True:
        delta = 0
        for s in range(env.nS):
            v = 0
            for a, action_prob in enumerate(policy[s]):
                for prob, next_state, reward, done in env.P[s][a]:
                    v += action_prob * prob * (reward + gamma * V[next_state])
            delta = max(delta, np.abs(v - V[s]))
            V[s] = v
        if delta < theta:
            break
    return np.array(V)

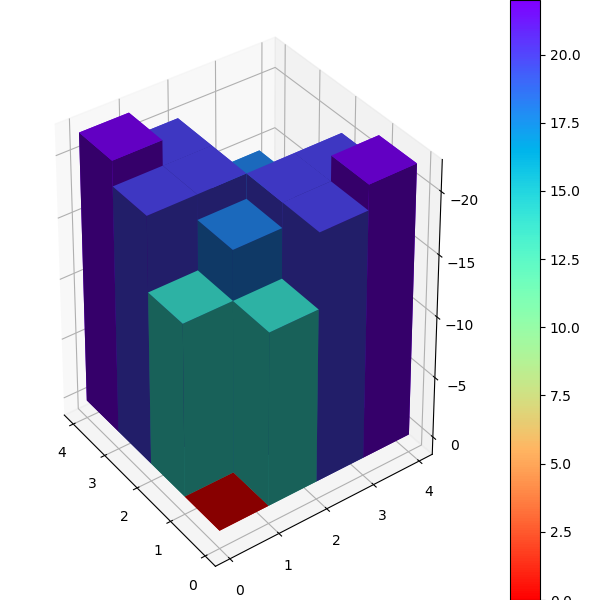
输入策略为随机选择方向，运行上面的policy_evaluate最终多轮收敛后的V值输出为

{linenos

[[  0.         -13.99931242 -19.99901152 -21.99891199]
 [-13.99931242 -17.99915625 -19.99908389 -19.99909436]
 [-19.99901152 -19.99908389 -17.99922697 -13.99942284]
 [-21.99891199 -19.99909436 -13.99942284   0.        ]]

在3D V值图中可以发现，由于是随机选择方向的策略， Agent在每个格子的V值绝对数值要比最佳V值大，意味着随机策略下Agent在Grid World会得到更多的负reward。

Grid World随机策略V值