从零构建统计随机变量生成器之正态分布 Box-Muller方法

7月 10 2021 Tech Blog 14 分钟读完 (约 2106 字)

在学习了一些基本的统计变量生成法之后，这次我们来看看如何生成正态分布。它就是大名鼎鼎的 Box-Muller 方法，Box-Muller 的理解过程可以体会到统计模拟的一些精妙思想。

尝试逆变换方法

我们先尝试通过标准的逆变换方法来生成正态分布。

正态分布的 PDF 表达式为

\[ f_Z(z) = \frac{1}{\sqrt{2 \pi}} \exp\left\{-\frac{z^2}{2}\right\} \]

对应的函数图形是钟形曲线

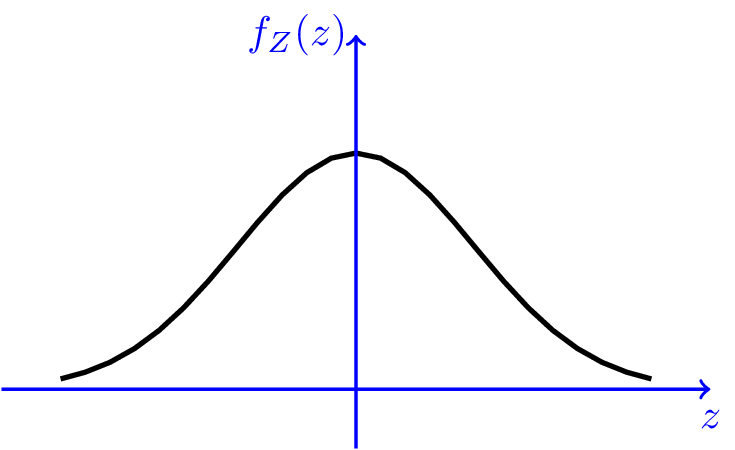
根据 PDF，其 CDF 的积分形式为 \[ \Phi(x)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{x} e^{-t^{2} / 2} d t \]

和所有 PDF CDF 关系一样，$\Phi(x)$ 表示 $f_Z$ 累积到 $x$ 点的面积。

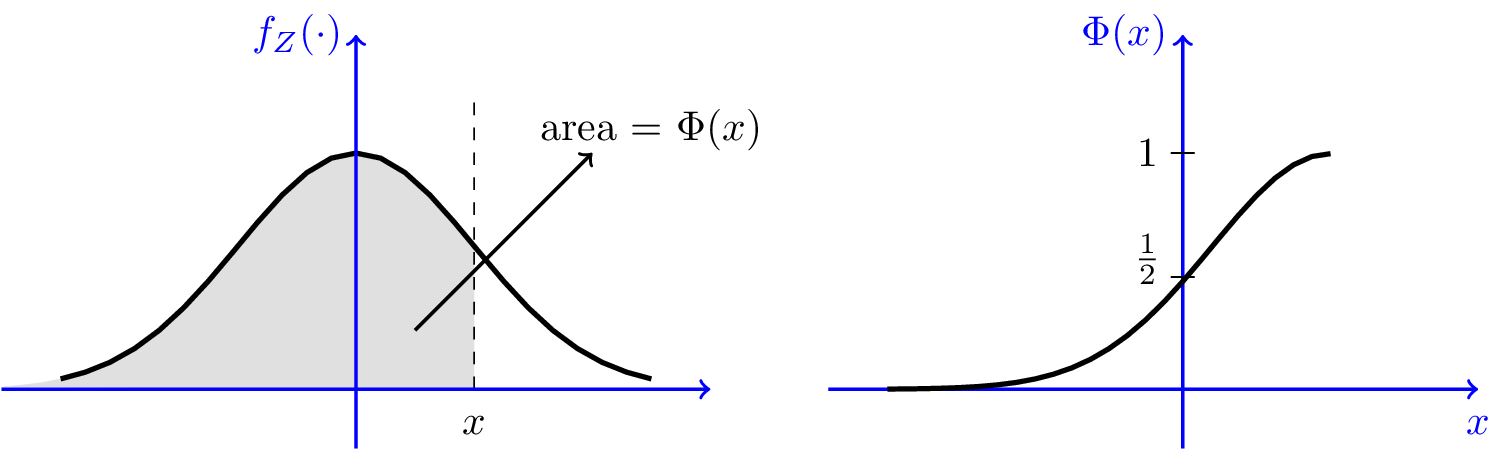
很不幸的是，$\Phi(x)$ 无法写出一般数学表达式，因而也无法直接用逆变换方法。

二维映射到一维

我们知道，高维正态分布有特殊的性质：它的每一维的分量都是正态分布；单个维度对于其他维度的条件概率分布也是正态分布。

用图来理解这两条性质就是，对于下图的二维正态分布 $ x = [x_1, x_2]^T $，单独的 $x_1$ 和 $x_2$ 都服从一维正态分布。

条件概率 $p(x_2|x_1 \approx1)$ 的PDF 对应图中的红线，显然也是一维正态分布。

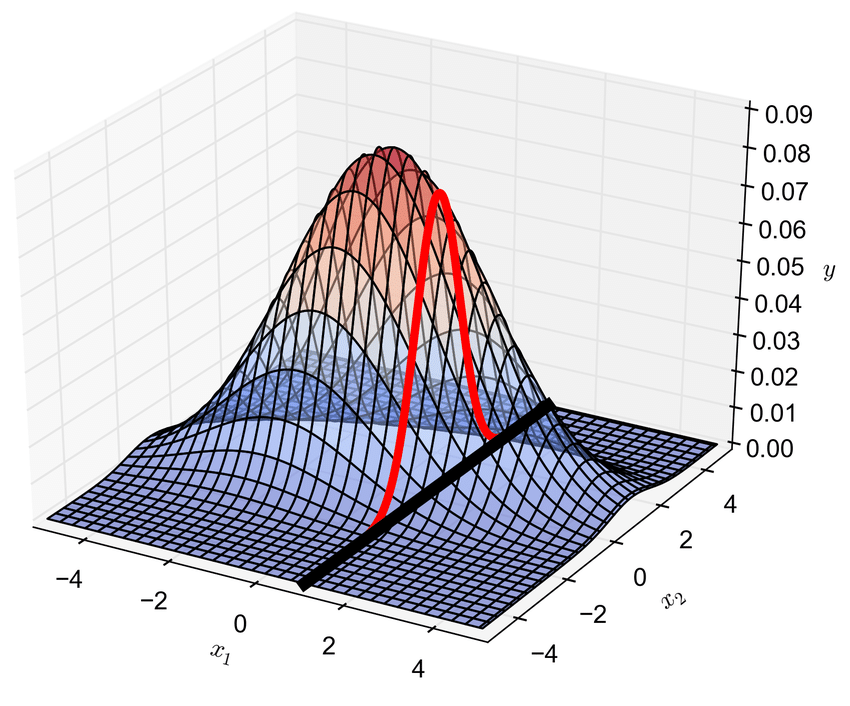
写一段简单的代码验证二维正态分布的单个分量服从正态分布。

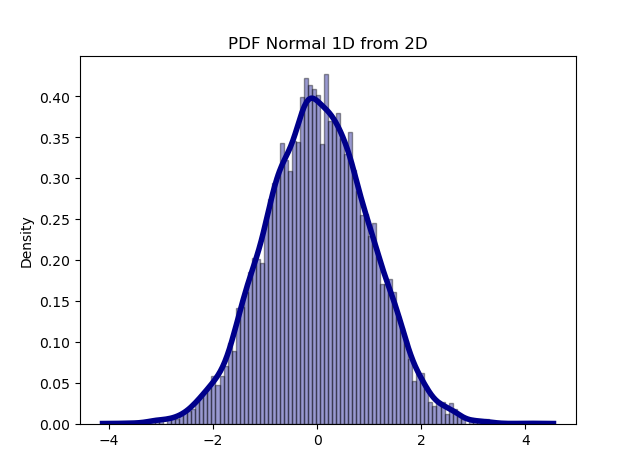
代码中，我们用np.random.normal生成了 10000 个服从二维正态分布的 x, y 点，然后我们丢弃 y，只保留 x，并画出 10000 个 x 的分布。

def plot_normal_1d():
    x, _ = np.random.normal(loc=0, scale=1, size=(2, 10000))
    import seaborn as sns
    sns.distplot(x, hist=True, kde=True, bins=100, color='darkblue',
                 hist_kws={'edgecolor': 'black'},
                 kde_kws={'linewidth': 4})
    plt.title('PDF Normal 1D from 2D')
    plt.show()

Box-Muller 原理

虽然无法直接用逆变换方法生成一维正态分布，但我们却能通过先生成二维的正态分布，利用上面一节的性质，生成一维正态分布。

而 Box-Muller 就是巧妙生成二维正态分布样本点的方法。

首先，我们来看看二维正态分布可以认为是两个维度是独立的，每个维度都是正态分布。此时，其 PDF 可以写成两个一维正态分布 PDF 的乘积。

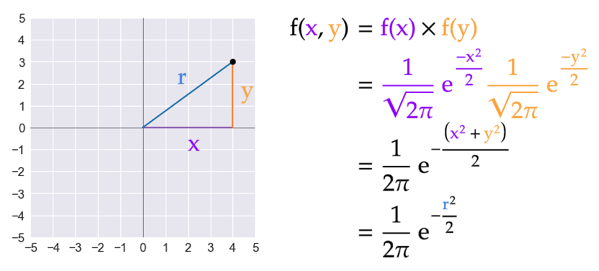
这种写法表明，二维正态分布仅用一个 r 向量就可以充分表达。注意，r 是向量，不仅有大小还有角度，有两个分量。这两个分量本质上是独立的，这就是 Box-Muller 方法的巧妙之处。也就是，Box-Muller 通过角度和半径大小两个分量的独立性分别单独生成并转换成 (x, y) 对。

角度分量是在 $2\pi$ 范围均匀采样，这一点比较直觉好理解。

再来看看半径分量 r。我们令 \[ s = {r^2 \over 2} \Longrightarrow r = \sqrt{2s} \]

则 s 服从指数分布 $\lambda=1$ 。

不信么？我们不妨来做个模拟实验，下图是模拟 10000次二维正态分布 (x, y) 点后转换成 s 的分布。

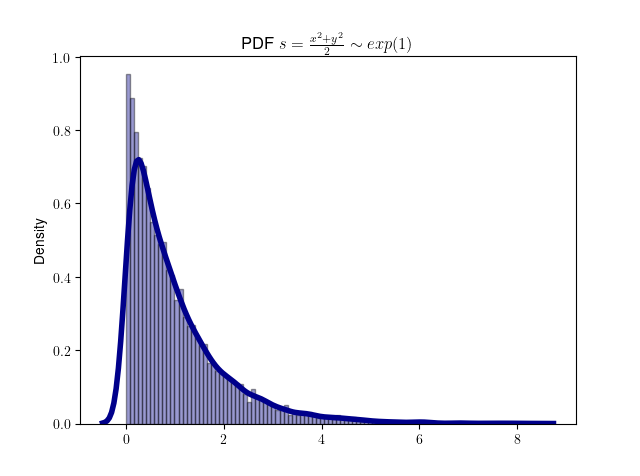
模拟和plot 代码如下

def plot_r_squared():
    def gen_normal_samples(n):
        x, y = np.random.normal(loc=0, scale=1, size=(2, n))
        return x, y

    x, y = gen_normal_samples(10000)
    s = (x * x + y * y)/2
    plot_dist_1d(s, title='PDF $s = {{x^2 + y^2}\over{2}} \sim exp(1)$')
    

def plot_dist_1d(X, title='PDF '):
    import seaborn as sns
    plt.rcParams.update({
        "text.usetex": True,
        "font.family": "sans-serif",
        "font.sans-serif": ["Helvetica"]})
    sns.distplot(X, hist=True, kde=True, bins=100, color='darkblue',
                 hist_kws={'edgecolor': 'black'},
                 kde_kws={'linewidth': 4})
    plt.title(title)
    plt.show()

确信了 s 符合指数分布，根据指数分布的 PDF，可以推出二维正态 PDF中的 $ e^{-r2/2}$ 也符合指数分布，即 \[ s \sim \exp(1) \Longrightarrow e^{-r^2/2} \sim \exp(1) \]

至此，总结一下Box-Muller方法。我们视二维正态分布PDF为独立两部分的乘积，第一部分是在 $2\pi$ 范围中的均匀分布，代表了二维平面中的角度 $\theta$，第二部分为 $\lambda=1$ 的指数分布，代表半径大小。

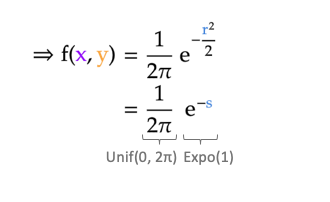
Box-Muller 方法通过两个服从 [0, 1] 均匀分布的样本 u1和u2，转换成独立的角度和半径样本，具体过程如下

生成 [0, 1] 的均匀分布 u1，利用逆变换采样方法转换成 exp(1) 样本，此为二维平面点半径 r
生成 [0, 1] 的均匀分布 u2，乘以 $2\pi$，即为样本点的角度 $\theta$
将 r 和 $\theta$ 转换成 x, y 坐标下的点。

理解了整个过程的意义，下面的代码就很直白。

def normal_box_muller():
    import random
    from math import sqrt, log, pi, cos, sin
    u1 = random.random()
    u2 = random.random()
    r = sqrt(-2 * log(u1))
    theta = 2 * pi * u2
    z0 = r * cos(theta)
    z1 = r * sin(theta)
    return z0, z1

接下来，我们来看看 Box-Muller 法生成的二维标准正态分布动画吧

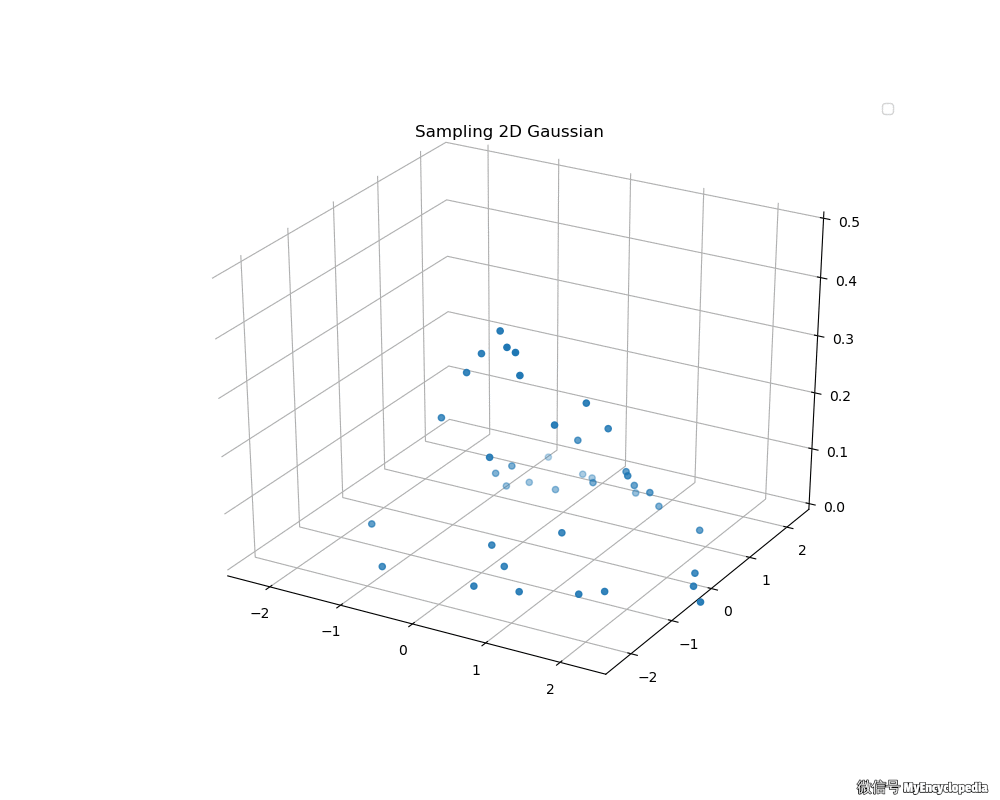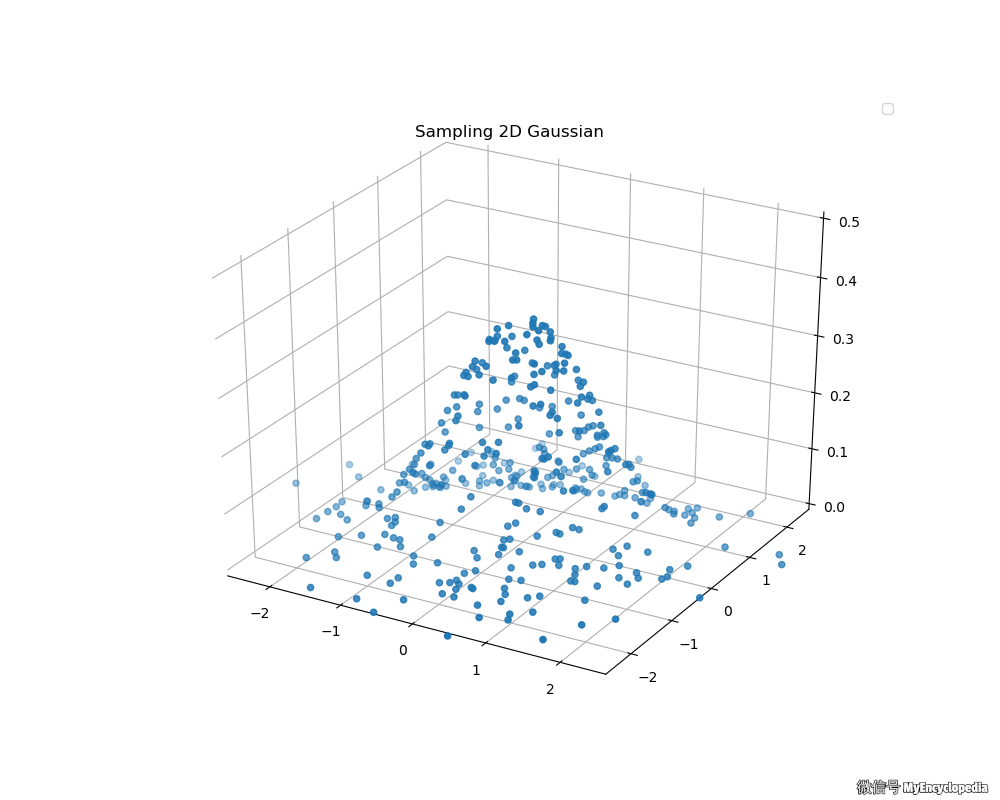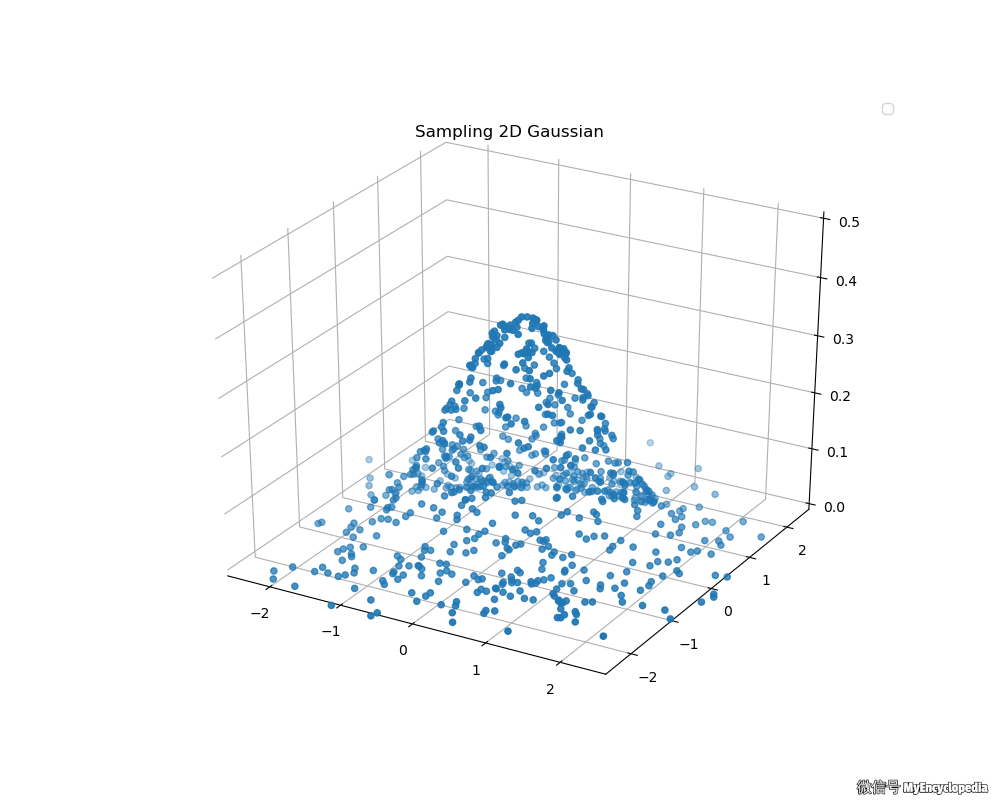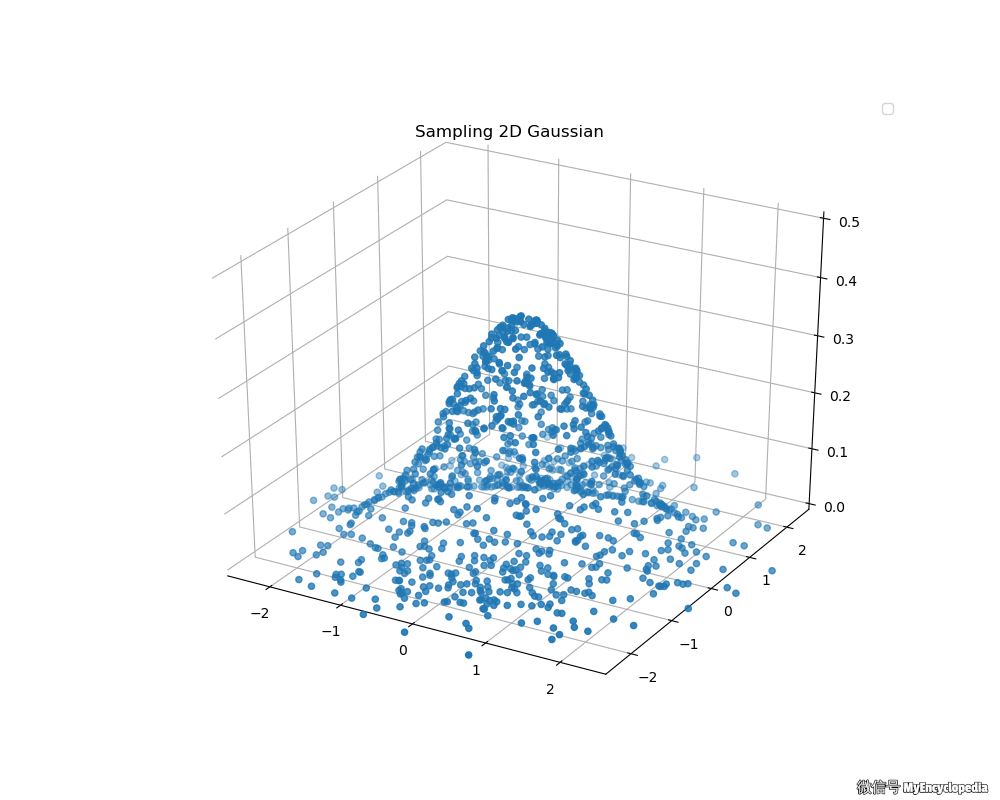
拒绝采样极坐标方法

Box-Muller 方法还有一种形式，称为极坐标形式，属于拒绝采样方法。

1. 生成独立的 u, v 和 s

分别生成 [0, 1] 均匀分布 u 和 v。令 $s = r^2 = u^2 + v^2$。如果 s = 0或 s ≥ 1，则丢弃 u 和 v ，并尝试另一对 (u , v)。因为 u 和 v 是均匀分布的，并且因为只允许单位圆内的点，所以 s 的值也将均匀分布在开区间 (0, 1) 中。注意，这里的 s 的意义虽然也为半径，但不同于基本方法中的 s。这里 s 取值范围为 (0, 1) ，目的是通过 s 生成指数分布，而基本方法中的 s 取值范围为 [0, +∞]，表示二维正态分布 PDF 采样点的半径。复用符号 s 的原因是为了对应维基百科中关于基本方法和极坐标方法的数学描述。

我们用代码来验证 s 服从 (0, 1) 范围上的均匀分布。

def gen_polar_s():
    import random
    while True:
        u = random.uniform(-1, 1)
        v = random.uniform(-1, 1)
        s = u * u + v * v
        if s >= 1.0 or s == 0.0:
            continue
        return s


def plot_polar_s():
    s = [gen_polar_s() for _ in range(10000) ]
    plot_dist_1d(s, title='PDF Polar $s = u^2 + v^2$')

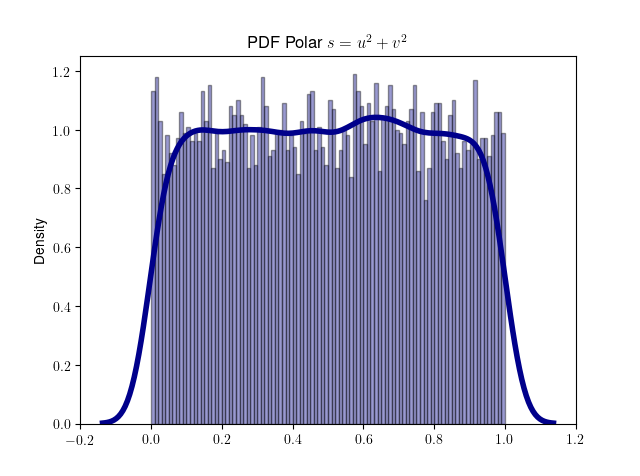
2. 将 u, v, s 转换成 x, y

若将 $s = R^2 uniform(0, 1) $ 看成是基本方法中的 u1，就可以用同样的方式转换成指数分布，用以代表二维PDF的半径。

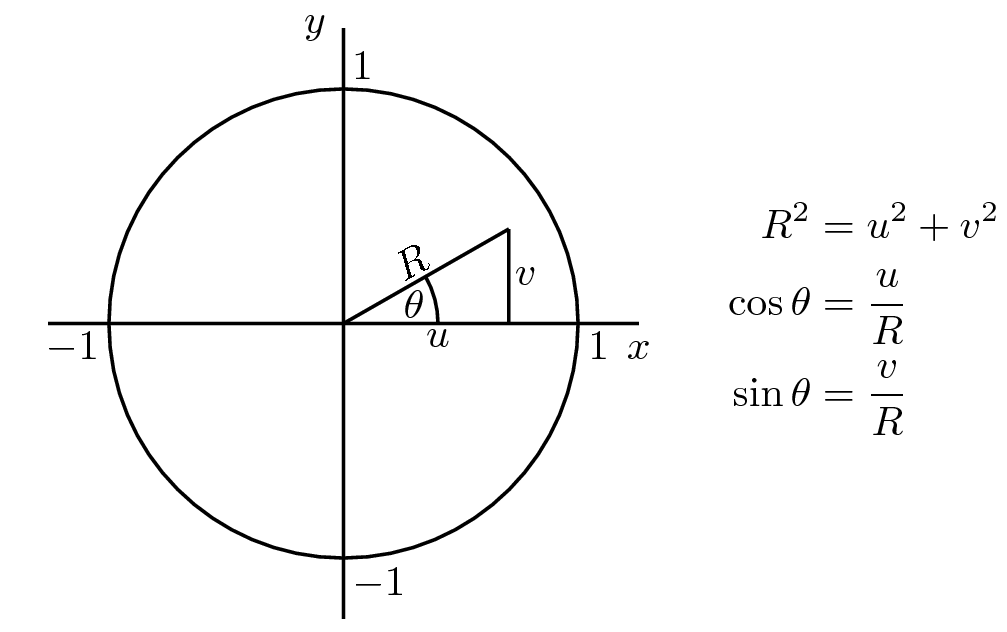
同时，根据下图，$\cos \theta$ 和 $\sin \theta$ 可以直接用 u, v, R 表示出来，并不需要通过三角函数显示计算出 $\theta$。有了半径， $\cos \theta$ 和 $\sin \theta$ ，则可以直接计算出 x, y 坐标，（下面用 $z_0, z_1$ 代替 $x, y$）。

\[ z_{0}=\sqrt{-2 \ln U_{1}} \cos \left(2 \pi U_{2}\right)=\sqrt{-2 \ln s}\left(\frac{u}{\sqrt{s}}\right)=u \cdot \sqrt{\frac{-2 \ln s}{s}} \]

\[ z_{1}=\sqrt{-2 \ln U_{1}} \sin \left(2 \pi U_{2}\right)=\sqrt{-2 \ln s}\left(\frac{v}{\sqrt{s}}\right)=v \cdot \sqrt{\frac{-2 \ln s}{s}} \]

同样，Box-Muller 极坐标方法的代码和公式一致。

def normal_box_muller_polar():
    import random
    from math import sqrt, log
    while True:
        u = random.uniform(-1, 1)
        v = random.uniform(-1, 1)
        s = u * u + v * v
        if s >= 1.0 or s == 0.0:
            continue
        z0 = u * sqrt(-2 * log(s) / s)
        z1 = v * sqrt(-2 * log(s) / s)
        return z0, z1

拒绝采样的效率

极坐标方法与基本方法的不同之处在于它是一种拒绝采样。因此，它会丢弃一些生成的随机数，但可能比基本方法更快，因为它计算更简单：避免使用昂贵的三角函数，并且在数值上更稳健。极坐标方法丢弃了生成总输入对的 1 − π /4 ≈ 21.46%，即需要 4/ π ≈ 1.2732 个输入随机数，输出一个随机采样。

#Python #Statistics #Simulation