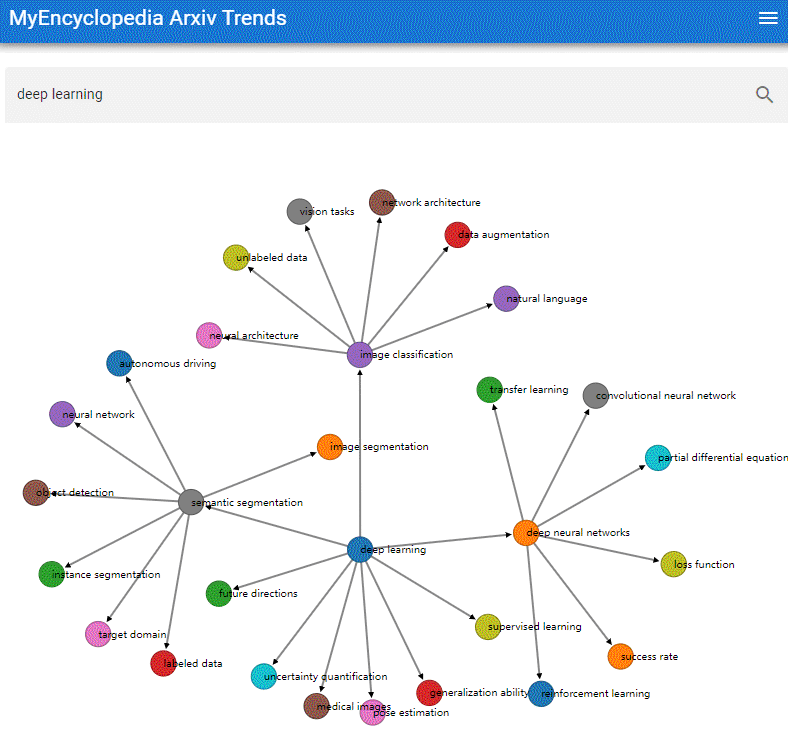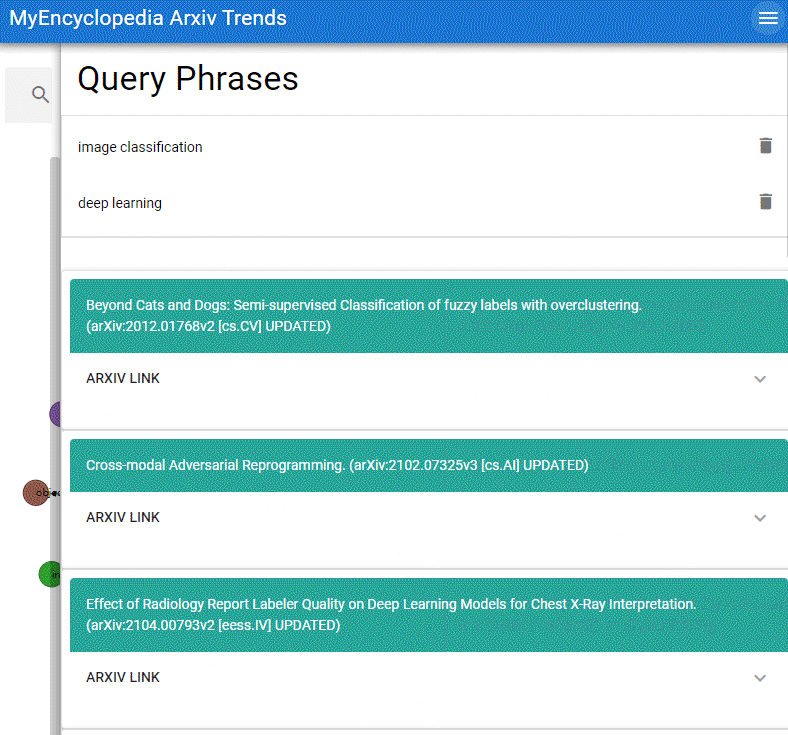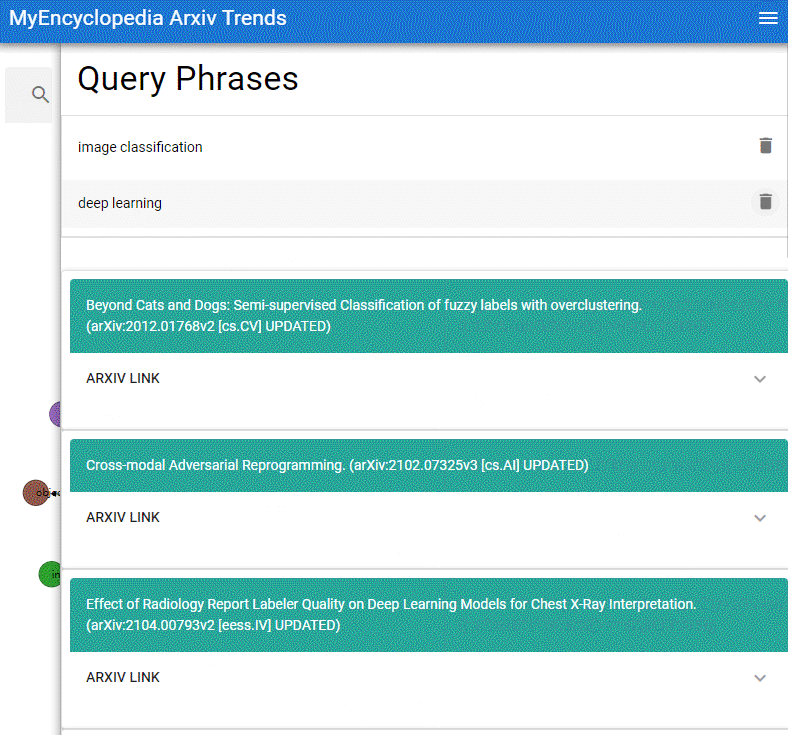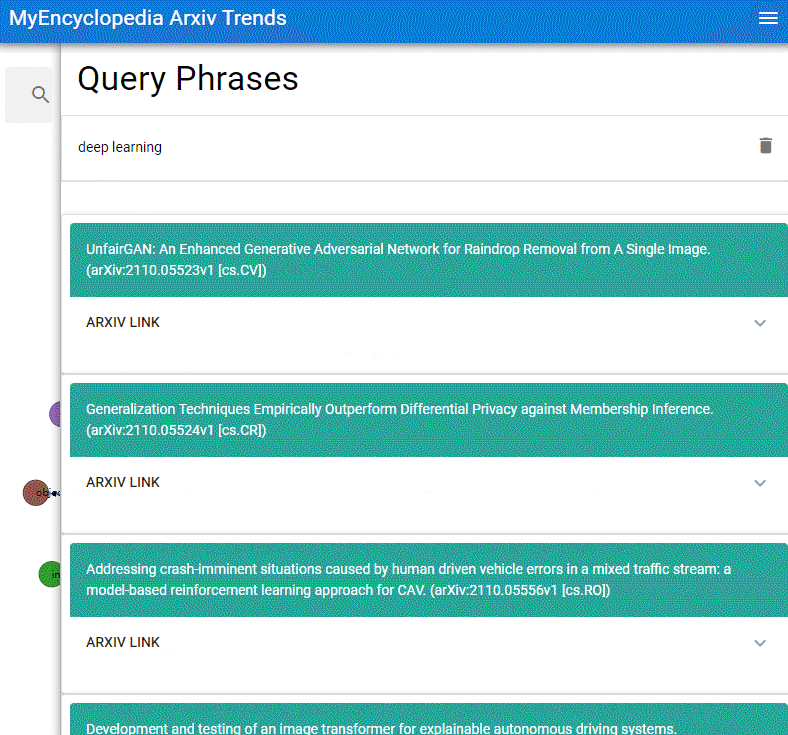
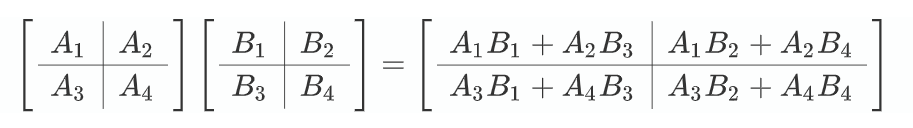本系列用彩色的 Latex 公式呈现总结 MIT Gilbert Strang 教授经典的线性代数课程18.06之精华,便于大家回顾复习。
Gauss-Jordan 算法是一种手工计算矩阵逆的技术。现在,你几乎不应该手动计算矩阵逆,即使是在计算机上,但 Gauss-Jordan 仍然有用,因为
它有助于我们理解逆矩阵何时以及为何存在。
它给了我们另一个例子来帮助我们理解消元的结构
回顾:矩阵的逆
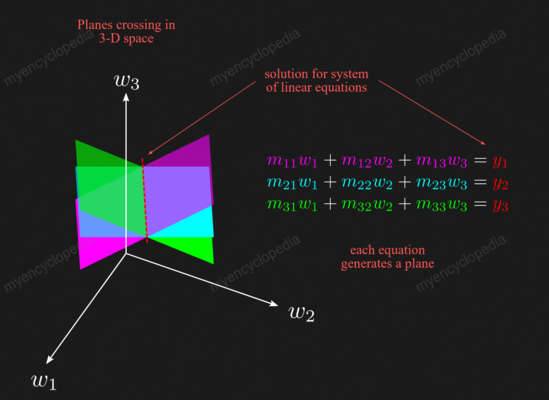
线性算子的 \(A^{-1}\) 是“撤消”操作的操作 \(A\) ,对于任何 \(x\),有:
即 \[\boxed{Ax=b \implies x = A^{-1} b}\]
这意味着
- 对于m×m 方阵 \(A\), \(A^{-1}\) 存在仅当 \(A\) 具有 m 个主元的
因为对于非方阵或具有一个或多个“零主元”的矩阵,我们不能总是解决 \(Ax=b\) (会在反向替换期间除以零)。也很容易看出 \(\boxed{(A^{-1})^{-1} = A}\) , 即 \(A\) 撤消操作 \(A^{-1}\) .
等价地
这里, \(I\) 是 m×m 单位矩阵——在线性代数中,我们通常从上下文来推断 \(I\) 的形状,但如果它是模棱两可时,可以写成 \(I_m\).
乘积的逆: (AB)⁻¹ = B⁻¹A⁻¹
很容易看出乘积 \(AB\) 的逆是两者逆的反向乘积:
\[\boxed{(AB)^{-1} = B^{-1} A^{-1}}\]
直观理解为,当反转一系列操作时,总是需要以倒序的顺序回溯操作。
容易证明这个结论,因为
例如,我们看到高斯消元对应于因式分解 \(A = LU\), 此时,\(U\) 是消除的结果,并且 \(L\) 只是消除步骤的记录。
然后
注意:逆允许我们“除以矩阵”,但我们总是要清楚我们是在左边还是右边。以下符号很方便,可用于 Julia 和 Matlab 中
通过线性方程求逆
方程 \(A A^{-1} = I\) 实际上给了我们计算的算法 \(A^{-1}\) .
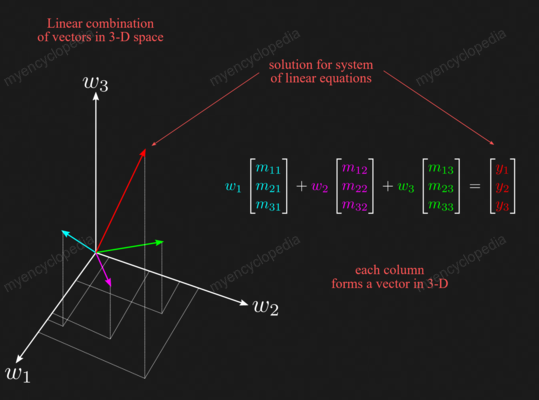
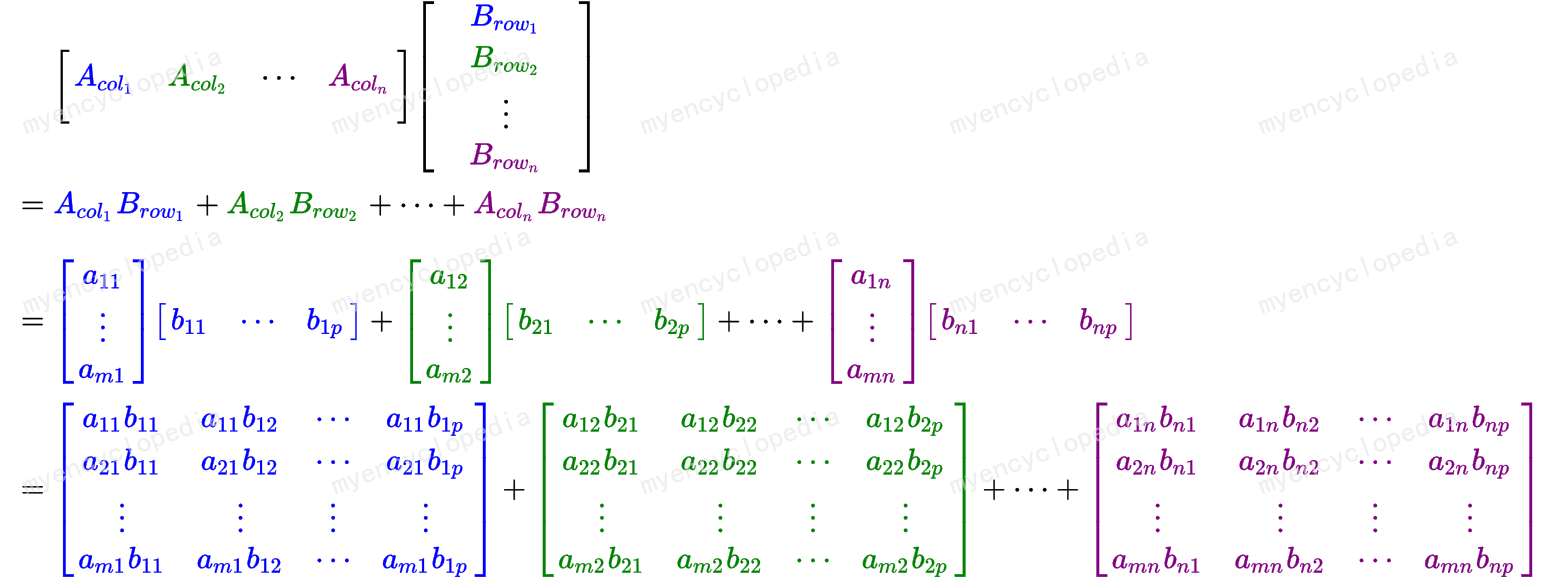
假设我们将 \(A\) 以及 \(I\) 表示成列的形式,即
那么
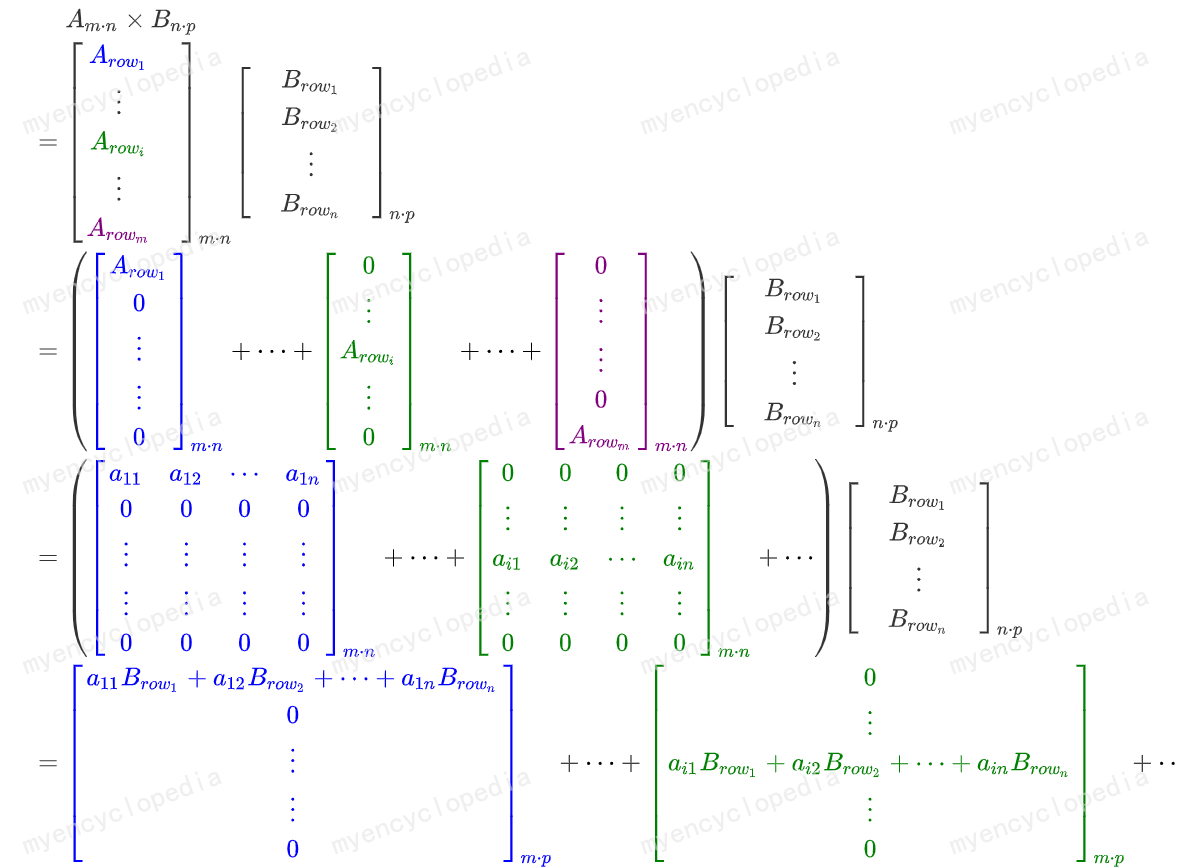
这里的关键事实是,将 \(A\) 乘以右侧的矩阵相当于将 \(A\) 乘以该矩阵的每一列,通过写出计算可以很容易地看到这一点。
如此,有了 m 个方程组,第 k 个方程组对应 \(A x_k = e_k\),解得这个方程组就可以得到 \(A^{-1}\) 的第 k 列 。也就是说,要找到 m×m 矩阵 \(A\) 的 \(A^{-1}\),我们必须求解 m 个 \(Ax=b\)。
换句话说,对于任何矩阵 \(B\) , \(Be_k\) 为 \(B\) 的第 k 列。 所以 \(A^{-1}\) 第 k 列是 \(x_k = A^{-1} e_k\) ,即 \(Ax_k = e_k\) 的解
理想情况下,当我们进行一次高斯消元 \(A=LU\) 后,就可以计算出 \(x_k = U^{-1} L^{-1} e_k\) ,做法是通过在 \(I\) 的每一列上做向前和向后替换(这本质上是计算机的做法)。
举例计算 L⁻¹ = E
例如,我们如何计算我们在上一课中从高斯消元中得到的 \(L\) 矩阵的逆矩阵,我们知道,结果应该是 \(L^{-1} = E\)
对于每个 \(e_1,e_2,e_3\),我们解对应方程组
\(e_k\) 是 3×3 \(I\) 的第 k 列。
例如对于 \(e_1\), 找到第一列 \(x_1\) 的 \(L^{-1} = E\):
The Gauss–Jordan 算法
Gauss-Jordan 可以被视为求解的一种技巧(主要用于手工计算)\(A b_k = e_k\). 但是用代数的方式思考也很好——这是我们高斯消元的“矩阵观点”的一个很好的应用。
简而言之,Gauss-Jordan 的想法是:如果我们对 \(A\) 执行一些行操作以获得 \(I\),那么对 \(I\) 执行相同的行操作会得到 \(A^{-1}\)。为什么?
行操作对应于从 \(A\) 左边乘以一组矩阵 \(E=\cdots E_2 E_1\)
所以,对 \(A\) 做行操作将其变成 \(I\) 意思等价于 \(EA = I\), 因此 \(E = A^{-1}\) .
对 \(I\) 执行相同的行操作,相当于 \(I\) 左乘矩阵 \(E\) , 即 \(EI\),因为 \(EI = E\) 并且 \(E = A^{-1}\),所以结果就是 \(A^{-1}\)
这就是我们可以用扩展矩阵来进行高斯消除,对 \(A\) 和 \(I\) 同时执行相同的行操作,即
\(A \to I\) 消除步骤
下面是具体将 \(A\) 通过行操作变换成 \(I\) 的步骤
- 做普通高斯消元“向下”将 \(A\) 转变成 \(U\) (上三角矩阵)。
- 然后,做高斯消去“向上” \(U\) 消除对角线以上的元素,将 \(U\) 转换成对角矩阵 \(D\)
- 最后,将 \(D\) 的每一行除以对角线元素值,得到 \(I\)
Gauss-Jordan 示例
让我们执行这些 \(A \to I\) 消除步骤 \(3 \times 3\) 矩阵 \(A\) : 先向下消除获得 \(U\) , 然后向上消除得到 \(D\) ,最后除以对角线元素值得到 \(I\):
没问题!很容易看出,只要 \(A\) 具有所有主元(即它是非奇异的),这将起作用。
永远不要计算矩阵逆!
矩阵逆很有趣,它在分析操作中非常方便,因为它们允许您轻松地将矩阵从方程的一侧移动到另一侧。但是,在“严肃的”数值计算中几乎从不计算逆矩阵。每当你看到 \(A^{-1} B\) 或者 \(A^{-1} b\),当您在计算机上实现它时,您应该阅读 \(A^{-1} B\) 作为“解决 \(AX = B\) 通过某种方法。”例如,通过 \(A \backslash B\) 或通过首先计算 \(LU\) 分解来解决它 \(A\) 然后用它来解决 \(AX = B\) .
你通常不计算逆矩阵的一个原因是它很浪费:一旦你有 \(A=LU\)(稍后我们将把它概括为“\(PA = LU\)"),你可以解决 \(AX=B\) 直接不用找 \(A^{-1}\), 和计算 \(A^{-1}\) 如果您只需要解决几个右手边,则需要更多的工作。
另一个原因是,对于很多特殊的矩阵,有办法解决 \(AX=B\) 比你能找到的要快得多 \(A^{-1}\). 例如,实践中的许多大矩阵是稀疏的(大部分为零),通常对于稀疏矩阵,您可以安排 \(L\) 和 \(U\) 也要稀疏。稀疏矩阵比一般的“密集”矩阵更有效,因为您不必乘以(甚至存储)零。即使 \(A\) 是稀疏的,然而, \(A^{-1}\) 通常是非稀疏的,因此如果计算逆矩阵,则会失去稀疏的特殊效率。
例如:
如果你看到 \(U^{-1} b\) 在哪里 \(U\) 是上三角,不用计算 \(U^{-1}\) 明确!只要解决 \(Ux = b\) 通过反向替换(从底行向上)。
如果你看到 \(L^{-1} b\) 在哪里 \(L\) 是下三角,不用计算 \(L^{-1}\) 明确!只要解决 \(Lx = b\) 通过前向替换(从顶行向下)。