Strang MIT 18.06 线性代数精髓 02：解方程组的意义和过程

本文继续以彩色Latex 方式总结了方程组的行视角，列视角的几何意义；并回顾了解方程的两个步骤：消元和回代。内容对应于MIT 18.06 Gilbert Strang 线性代数视频课程第一，二节。

本系列链接如下

01 - 矩阵乘法的五种理解

02 - 解方程组的意义和过程

方程组两种几何解释

二元方程组

来看一个具体的二元线性方程组

\[ \begin{cases} 2x&-y&=0 \\ -x&+2y&=3 \end{cases} \]

写成矩阵形式

\[ \begin{bmatrix} 2&-1 \\ -1&2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix} \]

行视角

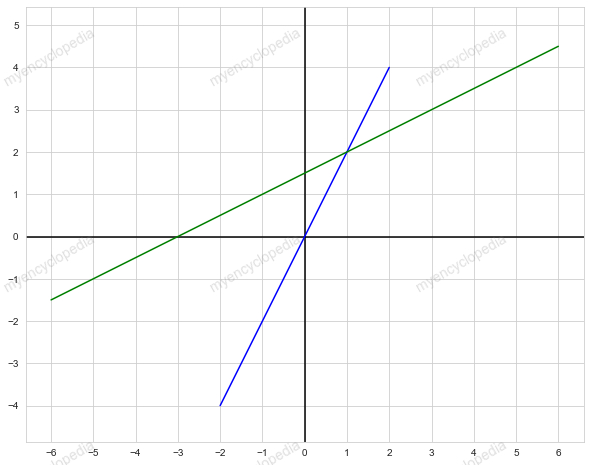
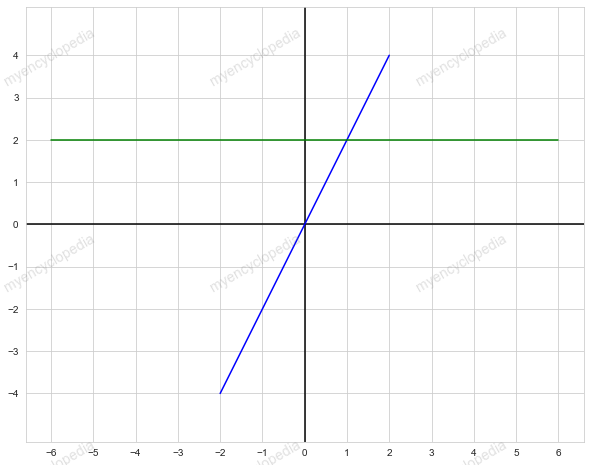
回顾 $2x - y = 0 $ 为所有满足此条件的 (x, y) 的集合，即集合组成二维平面的一条直线，如下图蓝线所示。

$ -x + 2y = 3$ 则对应绿线。

因此方程组的解 x = 1, y = 2 为两条直线的交点，这就是方程组的行视角：将系数矩阵按行切分，则每一行表示一个约束条件，几何意义是N维空间的一个子空间。在二元方程中，一行表示一条线，三元方程中，一行表示一个平面（详见后一小节）。 \[ \begin{bmatrix} \color{blue} 2 x & {\color{blue} -1 y} \\ \color{green} -1 x & \color{green} 2 y \end{bmatrix} = \begin{bmatrix} \color{blue} 0 \\ \color{green} 3 \end{bmatrix} \]

列视角

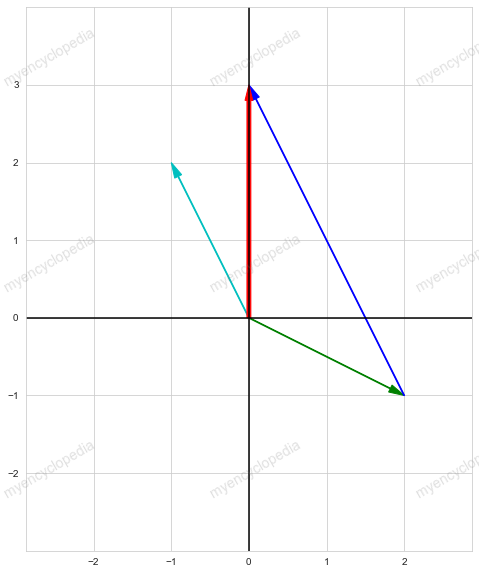
若将系数矩阵按列切分，则每一列表示一个向量，方程组的解 (x, y) 表示每个列向量以 x, y 为权重的线性组合刚好形成 b 向量。这个就是方程组 \(Ax=b\) 有解的条件：b 在 A 的列空间，此时，x 为 列向量的组合系数。 \[ x \begin{bmatrix} \color{Green} 2 \\ \color{Green} -1 \end{bmatrix} + y \begin{bmatrix} \color{Turquoise} -1 \\ \color{Turquoise} 2 \end{bmatrix} = \begin{bmatrix} \color{Red} 0\\ \color{Red} 3 \end{bmatrix} \]

三元方程组

行视角

对于三元方程组行视角来说，每一行的方程组成一个三维空间中的一个平面。解是三个平面的交点，通常来说为一个点。 \[ \begin{bmatrix} \color{magenta} m_{11} & \color{magenta} m_{12} & \color{magenta} m_{13} \\ \color{cyan} m_{21} & \color{cyan} m_{22} & \color{cyan} m_{23} \\ \color{green} m_{31} & \color{green} m_{32} & \color{green} m_{33} \\ \end{bmatrix} \begin{bmatrix} w_{1} \\ w_{2} \\ w_{3} \end{bmatrix}= \begin{bmatrix} \color{magenta} y_{1} \\ \color{cyan} y_{2} \\ \color{green} y_{3} \end{bmatrix} \]

图片来自 Introduction to Linear Algebra for Applied Machine Learning with Python，解为一直线而非一个点。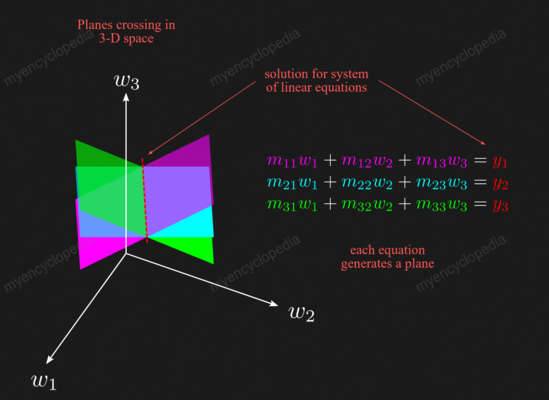

列视角

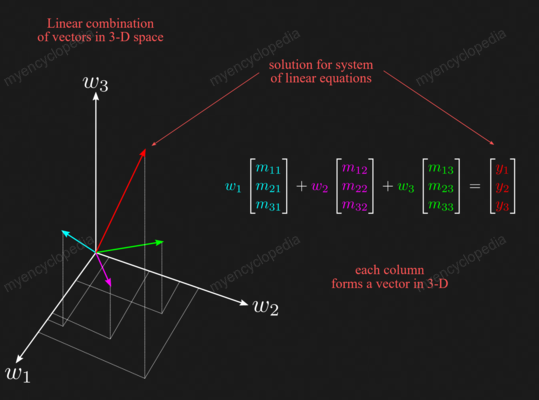
三元列视角下，A 的列向量为三维平面的一个向量，x（下图为 w） 表示每个列向量取多少倍数可以组成 b 向量。 \[ \color{cyan} w_1 \color{black} \begin{bmatrix} \color{cyan} m_{11} \\ \color{cyan} m_{21} \\ \color{cyan} m_{31} \end{bmatrix}+ \color{magenta} w_2 \color{black} \begin{bmatrix} \color{magenta} m_{12} \\ \color{magenta} m_{22} \\ \color{magenta} m_{32} \end{bmatrix}+ \color{green} w_3 \color{black} \begin{bmatrix} \color{green} m_{13} \\ \color{green} m_{23} \\ \color{green} m_{33} \end{bmatrix}= \begin{bmatrix} \color{red} y_{1} \\ \color{red} y_{2} \\ \color{red} y_{3} \end{bmatrix} \]

解方程的步骤

总结了二元三元方程组的行和列视角后，我们回顾求解方程的具体步骤。用两个过程，消元和回代便可以解得方程。

• 消元的目的是将系数矩阵表示成变量依次依赖的上矩阵形式 (Upper Triangular Matrix)。 \[ \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{bmatrix} \underrightarrow{Eliminate} \begin{bmatrix} \color{red} a_{11} & a_{12} & \cdots & a_{1n} \\ \color{gray} 0 & \color{red} a'_{22} & \cdots & a'_{2n} \\ \color{gray} 0 & \vdots & \ddots & \vdots \\ \color{gray} 0 & \color{gray} 0 & \color{gray} 0 & \color{red} a'_{nn} \\ \end{bmatrix} \]

• 回代则在上矩阵的基础上依次解得每个分量的值。

三元方程示例

举个三元方程组为例 \[ \begin{cases} x&+2y&+z&=2 \\ 3x&+8y&+z&=12 \\ &+4y&+z&=2 \end{cases} \]

写成矩阵形式为

\[ \begin{bmatrix}1&2&1\\3&8&1\\0&4&1\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}2\\12\\2\end{bmatrix} \]

消元过程

在消元过程中，有两类操作，一是将上一行乘以某系数后被下一行减去，依次消除这一行的元。第二类操作是交换当前行和后面某行，行交换用于当某行对应的元已经为0的情况下。

以上述三元方程为例，第二行消元的具体过程为第二行减去3倍的第一行。接着，再进行第三行消元。

\[ \left[\begin{array}{c|c}A&b\end{array}\right] = \left[\begin{array}{ccc|c} \color{red} 1&2&1&2 \\ 3&8&1&12 \\ 0&4&1&2 \end{array}\right] \xrightarrow{row_2-3row_1} \left[\begin{array}{ccc|c} \color{red} 1&2&1&2 \\ \color{blue} \boxed{0} & \color{red} 2& \color{blue} -2& \color{blue}6 \\ 0&4&1&2 \end{array}\right] \xrightarrow{row_3-2row_2} \left[\begin{array}{ccc|c} \color{red}1&2&1&2 \\ 0& \color{red} 2&-2&6 \\ \color{blue} 0 & \color{blue} \boxed{0} & \color{red} 5& \color{blue}-10 \end{array}\right] \]

最终，上矩阵为 \[ U=\begin{bmatrix} \color{red} 1 & 2& 1 \\ \color{gray} 0 & \color{red} 2 & -2 \\ \color{gray} 0 & \color{gray} 0& \color{red} 5 \end{bmatrix} \]

回代过程

回代过程比较直白，由上矩阵 U 对应方程组 \[ \begin{cases} \color{red} x&+2y&+z&=2 \\ & \color{red} +2y &-2z&=6 \\ && \color{red} +5z&=-10 \end{cases} \]

自下向上，容易解得 \[ \begin{cases} \color{red}x \color{black}= 2 \\ \color{red}y \color{black}= 1 \\ \color{red}z \color{black}= -2 \end{cases} \]

消元的行视角意义

注意到消元时的两类操作都不改变系数矩阵的行空间，只是改变了行空间的线性组合方式。

由于每一行代表一个拘束子空间，因此每一次消元改变了该行的拘束子空间。

举个例子，对于二元方程组和行空间 \[ \begin{bmatrix} \color{blue} 2 x & \color{blue} -1 y \\ \color{green} -1 x & \color{green} 2 y \end{bmatrix} = \begin{bmatrix} \color{blue} 0 \\ \color{green} 3 \end{bmatrix} \]

对应了两条直线

第二行的 x 消除后其几何意义为：蓝色直线不变，绿色直线从包含 x 的成分变成不含 x 成分，并且维持交点 （1, 2）不变。 \[ \begin{bmatrix} \color{blue} 2 x & \color{blue} -1 y \\ & \color{green} {3 \over 2} y \end{bmatrix} = \begin{bmatrix} \color{blue} 0 \\ \color{green} 3 \end{bmatrix} \]

最后还有一个问题可以思考一下：消元对于列视角的几何意义是什么呢？