在 MIT Gilbert Strang 教授经典的线性代数课程第三节中详细解释了矩阵相乘的5种方法及其理解,本文用彩色的 Latex 公式呈现出来,便于大家回顾复习。
假定 \(A \times B =C\) 中, A 是 \(m\) 行 \(n\) 列的矩阵, \(B\) 是 \(n\) 行 \(p\) 列的矩阵,\(C\) 为 \(m\) 行 \(p\) 列矩阵:
\[ A_{m \cdot n} \times B_{n \cdot p} = C_{m \cdot p} \]
B矩阵的列组合:列列切分
这是最经典的理解方式,沿袭了第一部分 \(A \vec x= \vec b\) 的方式。
回顾可以将 \(A \vec x\) 视为 \(A\) 的列向量关于每个 \(x\) 分量的线性组合。
那么 \(A B\) 相乘可以理解为将矩阵 \(B\) 按列切分成列向量,即 \[ B = [\vec B_{col_1} \vec B_{col_2} \cdots \vec B_{col_p} ] \]
如此,结果矩阵的第 \(j\) 列就是 \(A \vec B_{col_j}\):\(A\) 的列向量关于 $ B_{col_j} $ 的线性组合。

由于我们将 \(A\) 和 \(B\) 都按列来切,这种方式可以助记成 列列 切分。
A矩阵行组合:行行切分
同样的,对应与 \(A\) 右乘向量等同于\(A\)列的组合,\(A\) 左乘行向量等同于 \(A\) 行的组合: \[ [x_1, x_2, ..., x_n]\begin{bmatrix} A_{row_1} \\ A_{row_2} \\ \vdots \\A_{row_n} \end{bmatrix} = x_1 \cdot A_{row_1} + x_2 \cdot A_{row_2} +...+ x_n \cdot A_{row_n} \] 其结果是一个行向量。
那么 \(A B\) 相乘可以理解为将矩阵 \(A\) 按行切分成行向量,即 \[ A = \begin{bmatrix} A_{row_1} \\ A_{row_2}\\ \vdots \\ A_{row_m} \end{bmatrix} \]
如此,结果矩阵的第 \(i\) 行就是 \(\vec A_{row_i} B\):\(B\) 的行向量关于 $ A_{row_i} $ 的线性组合。
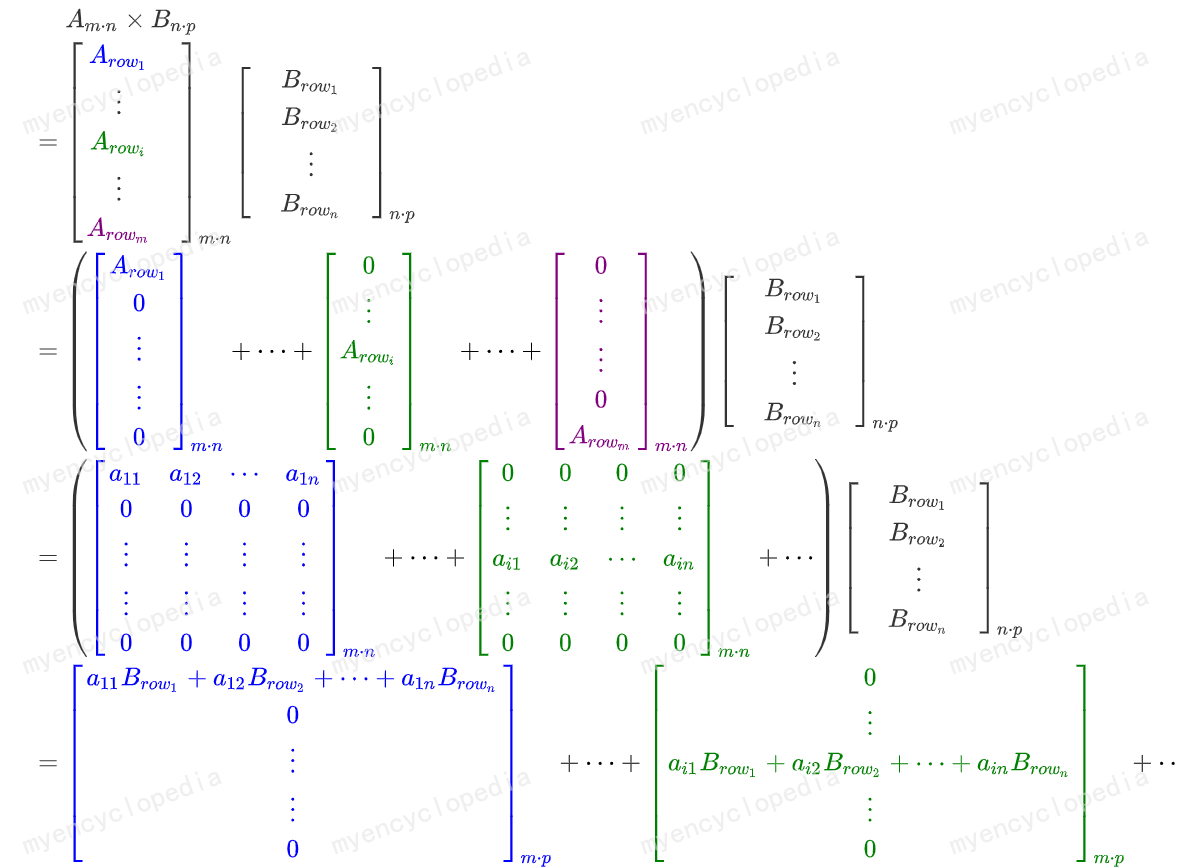
这种方式可以助记成 行行 切分。
A行 x B列 点乘:行列切分
如 \(A\) 矩阵按行切,\(B\) 矩阵按列切,即住记成 行列 切分时如下所示。
\[ \begin{eqnarray*} && A_{m \cdot n} \times B_{n \cdot p} \\ &=& \begin{bmatrix} A_{row_1} \\ A_{row_2} \\ \vdots \\ A_{row_i} \\ \vdots \\ \end{bmatrix}_{m \cdot n} \begin{bmatrix} B_{col_1} & B_{col_2} & \cdots & B_{col_p} \end{bmatrix}_{n \cdot p} \\ &=& \begin{bmatrix} &\vdots&\\& A_{row_i}&\\&\vdots& \end{bmatrix}_{m \cdot n} \begin{bmatrix} &&\\\cdots& B_{col_j} & \cdots\\&& \end{bmatrix}_{n \cdot p} \\ &=& \begin{bmatrix} &\vdots&\\\cdots&c_{ij}&\cdots\\& \vdots \end{bmatrix}_{m \cdot p} \end{eqnarray*} \]
行乘以列即列向量点乘,结果是一个标量。因此 \(c_{ij}\) 为结果矩阵 \(C\) 的第 \(i\) 行 \(j\) 列的值。
\[ c_{ij}=A_{row_i} \cdot B_{col_j} = \begin{bmatrix} a_{i1} & a_{i2} & \cdots & a_{in} \end{bmatrix} \begin{bmatrix} b_{1j} \\ b_{2j} \\ \vdots \\ b_{nj} \end{bmatrix} =\sum_{k=i}^na_{ik}b_{kj} \]
A列 x B行 矩阵和:列行切分
最后,也可也按列行来切分。注意列乘以行时的结果是一个矩阵。
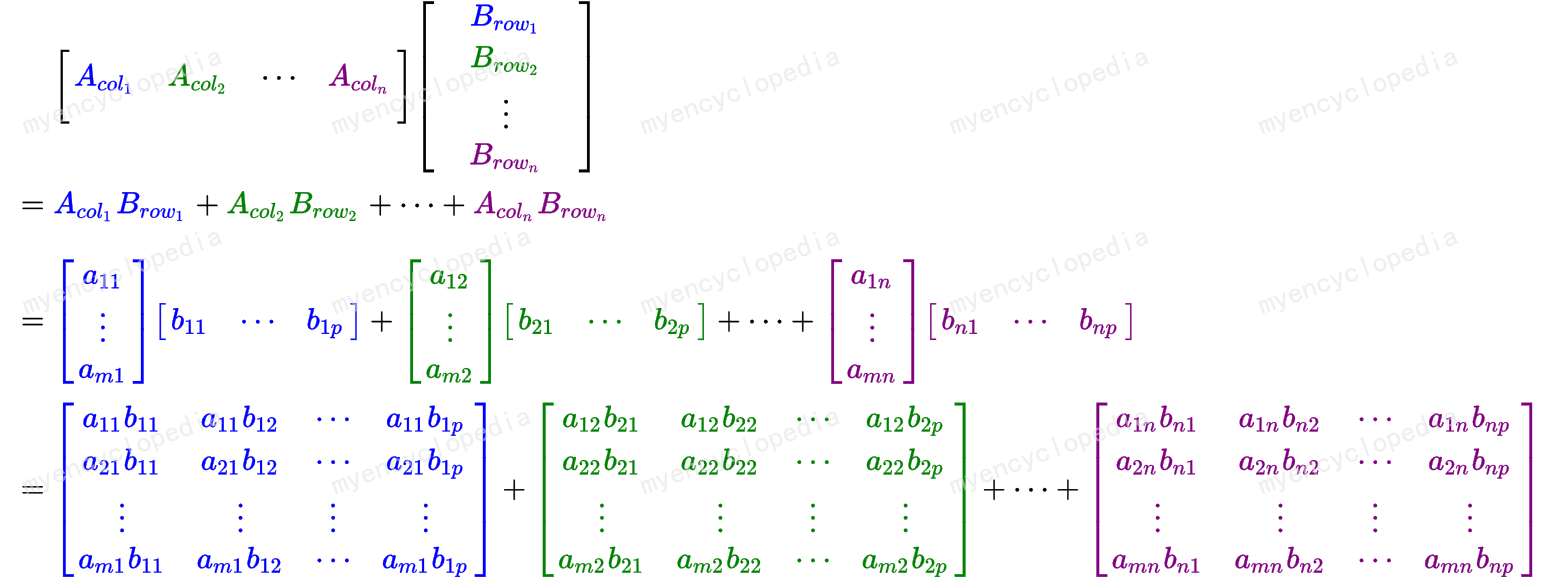
分块相乘
第五种方式是分块相乘,可以认为是点乘理解下的扩展。
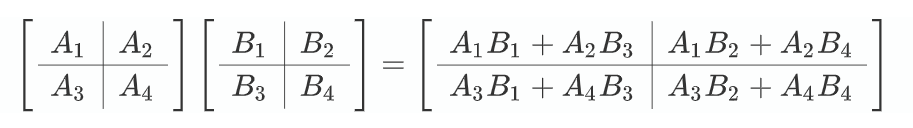

评论
shortnamefor Disqus. Please set it in_config.yml.